斜率优化 dp
先看例题理解。
任务安排
\(O(n^2)\) dp
设 \(dp_i\) 表示前 \(i\) 个物品被分批后的最小总费用,同时处理开机时间 \(s\) 对后面状态的影响,则有转移 \(dp_i=\min_{j=0}^{i-1} dp_j + \sum_{k=1}^i t_k \times \sum_{k=j+1}^i f_k + s \times \sum_{k=j+1}^n f_k\),显然可以预处理出来前缀和求解,变为:\(dp_i = \min_{j=0}^{i-1} dp_j + t_i \times (f_i-f_j)+ s \times (f_n -f_{j})\)。
时间复杂度 \(O(n^2)\)。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define INT_MAX (1e18)
const int N=5e3+10;
int n,s;
int a[N],b[N],dp[N];
inline int read(){
int t=0,f=1;
register char c=getchar();
while (c<48||c>57) f=(c=='-')?(-1):(f),c=getchar();
while (c>=48&&c<=57)t=(t<<1)+(t<<3)+(c^48),c=getchar();
return f*t;
}
void solution(){
/*
*/
}
signed main(){
n=read(),s=read();
for(int i=1;i<=n;i++) a[i]=read(),b[i]=read();
for(int i=1;i<=n;i++) a[i]+=a[i-1],b[i]+=b[i-1];
for(int i=1;i<=n;i++){
int minn=INT_MAX;
for(int j=0;j<i;j++)
minn=min(minn,dp[j]+a[i]*(b[i]-b[j])+s*(b[n]-b[j]));
dp[i]=minn;
cout<<dp[i]<<" ";
}
cout<<dp[n]<<"\n";
return 0;
}
\(O(n \log n)\) dp
将原先的式子变形:
考虑对于 \(j>j1\),什么时候 \(j\) 不优于 \(j1\)。
发现这个东西很像斜率表达式,那不妨设 \(y_i = dp_i,x_i=f_i\),则原式要求即为 \((x_{j1},y_{j1})\) 与 \((x_{j},y_{j})\) 之间直线的斜率大于等于 \(s+t_i\)。
接下来看一张图:
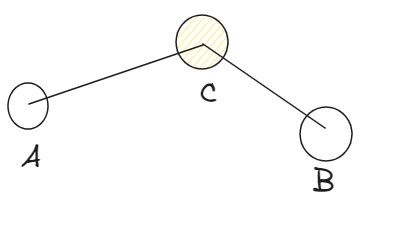
设 \(AC,CB\) 斜率分别为 \(k1,k2\),\(s-t_i\) 为 \(k0\)。首先有 \(k1>k2\),然后根据我们刚才的证明,有若 \(k1\le k0\),则 \(C\) 点优于 \(A\) 点,反之亦然;若 \(k2 \le k0\),则 \(B\) 点优于 \(C\) 点,反之亦然。
则现在有三种情况:
- \(k0 \le k2 < k1\),则 \(C\) 不优于 \(A\) 点。
- \(k2 \le k0 \le k1\),则 \(C\) 不优于 \(B\) 点。
- \(k2 < k1 \le k0\),则 \(C\) 既不优于 \(A\) 也不优于 \(B\)。
综上,上述情况下,\(C\) 一定会被踢出决策候选点,所以最后是一个下凸包的结构。
现在只剩下两个关键问题:如何维护下凸包和对于每个 \(i\) 如何找到答案。
维护凸壳可以使用单调队列维护,队列中始终保持一个凸包的形状,那么每加入一个,只需找到相邻的两个点,并判断他们的斜率关系即可,注意要一直弹出队头(尾),知道剩下的图形是一个凸包。因为每新加入一个点,可能需要删除多个点才可以变为一个凸包。
那么对于每个 \(i\) 如何找到答案呢?考虑之前证明出第 \(j\) 个点与第 \(j1(j<j1)\) 个点连线的斜率大于等于 \(s+t_i\) 时,第 \(j\) 个点更优,又因为凸壳斜率单增,所以只需要二分找到第一个大于等于 \(s+t_i\) 的点即可。
时间复杂度 \(O(n \log n)\)。
\(O(n)\) dp
发现凸包单增,\(s+t_i\) 单增,则维护指针记录即可。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define INT_MAX (1e18)
const int N=3e5+10;
int n,s,head,tail;
int a[N],b[N],id[N],dp[N];
inline int read(){
int t=0,f=1;
register char c=getchar();
while (c<48||c>57) f=(c=='-')?(-1):(f),c=getchar();
while (c>=48&&c<=57)t=(t<<1)+(t<<3)+(c^48),c=getchar();
return f*t;
}
void solution(){
/*
*/
}
double calc(int x,int y){
double xx=(double)(dp[y]-dp[x])/(double)(b[y]-b[x]);
return xx;
}
bool judge(int x,int y,int z){
if(calc(x,y)>calc(y,z)) return true;
return false;
}
void update(int x,int y){
dp[y]=a[y]*b[y]+s*b[n]+dp[x]-s*b[x]-a[y]*b[x];
}
signed main(){
n=read(),s=read(),head=1,tail=1;
for(int i=1;i<=n;i++)
a[i]=read(),b[i]=read();
for(int i=1;i<=n;i++) a[i]+=a[i-1];
for(int i=1;i<=n;i++) b[i]+=b[i-1];
int pos=1;
for(int i=1;i<=n;i++){
while(pos<tail&&calc(id[pos],id[pos+1])<s+a[i]) pos++;
update(id[pos],i);
while(tail>head&&judge(id[tail-1],id[tail],i)){
if(tail==pos) pos--;
tail--;
}
id[++tail]=i;
// cout<<dp[i]<<" ";
}
cout<<dp[n]<<"\n";
return 0;
}
加强版
此时发现 \(s+t_i\) 并不具备单调性,那么此时直接二分即可。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define INT_MAX (1e18)
const int N=3e5+10;
int n,s,head,tail;
int a[N],b[N],id[N],dp[N];
inline int read(){
int t=0,f=1;
register char c=getchar();
while (c<48||c>57) f=(c=='-')?(-1):(f),c=getchar();
while (c>=48&&c<=57)t=(t<<1)+(t<<3)+(c^48),c=getchar();
return f*t;
}
void solution(){
/*
*/
}
bool judge(int x,int y,int z){
if((dp[y]-dp[x])*(b[z]-b[y])>=(dp[z]-dp[y])*(b[y]-b[x])) return true;
return false;
}
void update(int x,int y){
dp[y]=a[y]*b[y]+s*b[n]+dp[x]-s*b[x]-a[y]*b[x];
}
bool check(int x,int y,int z){
return ((dp[y]-dp[x])>(z*(b[y]-b[x])));
}
int er(int x){
int l=1,r=tail-1,mid;
while(l<r){
mid=(l+r>>1);
if(check(id[mid],id[mid+1],x)) r=mid;
else l=mid+1;
}
if(check(id[l],id[l+1],x)) return id[l];
return id[l+1];
}
signed main(){
n=read(),s=read(),head=1,tail=1;
for(int i=1;i<=n;i++)
a[i]=read(),b[i]=read();
for(int i=1;i<=n;i++) a[i]+=a[i-1];
for(int i=1;i<=n;i++) b[i]+=b[i-1];
for(int i=1;i<=n;i++){
update(er(s+a[i]),i);
while(tail>1&&judge(id[tail-1],id[tail],i)) tail--;
id[++tail]=i;
}
cout<<dp[n]<<"\n";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号