整体二分
适用范围
整体二分是一种离线算法,当询问数较多但均具有单调性(即 \(x\) 合法则 \([1,x]\) 或 \([x,n]\) 均合法)时,设判断 \(x\) 是否合法的时间复杂度为 \(p\),则在不考虑预处理的情况下,所有询问能做到 \(O(q \log n \times p)\),一般 \(p\) 为 \(\log n\),所以总时间复杂度为 \(O(q \log^2 n)\)。但是每个询问的预处理时间较长,此时可以使用整体二分将多个询问整合在一起来统一预处理,从而减少时间复杂度。
以上纯感性理解()
例题
例题 \(1\) 静态区间第 \(k\) 小
给定 \(q\) 个询问,每次询问区间 \([l,r]\) 中第 \(k\) 小的值。
先考虑单次询问,对于单次询问有三种方法。
-
直接排序,输出第 \(k\) 个数。
-
将区间 \([l,r]\) 中的数都提前插入树状数组中,然后进行树状数组上二分。
-
二分第 \(k\) 小的值,设其为 \(x\),将区间 \([l,r]\) 中值域在 \([1,x]\) 中的数记录总和进行判断。
这三种方法均为单次询问 \(n \log n\),考虑哪种可以将询问整合在一起一块处理。
第一种显然不行,即便整合在一起也只能一个个排序;第二种也不太行,其与区间的左右边界强相关,而询问的左右边界并不相同;第三种似乎可以,因为每个询问都可以通过枚举第 \(k\) 小的值然后进行判断,但是其也是和区间左右边界有关,所以我们进行一下改动。
二分第 \(k\) 小的值,设其为 \(x\),将整个序列中值域在 \([1,x]\) 中的数记录在树状数组中,然后查询区间 \([l,r]\) 中数的个数进行判断。
改动之后预处理的操作对于所有操作都是一样的,只是判断的时候才需借用区间左右边界。此时就可以将操作整合在一起了。
考虑外面的二分不变,里面只对答案值域为 \([l,r]\) 的所有询问处理,直至 \(l=r\)。如下图所示:

发现像是一个线段树的结构,那就可以使用类似线段树的递归。
solve(int l,int r,vector<pair<int,int> > a,vector<node> q)
其中 \(l,r\) 代表的是 \(q\) 中所有询问的值域,\(a\) 序列中为值域在 \([l,r]\) 中的所有数,\(first\) 为数的位置,\(second\) 为数的值。
此时继续往下递归的时候需要将 \(q\) 分为两半,那么就可以使用之前所说的枚举 \(a\) 中的每一个数,若其 \(\le mid\),则插入树状数组中,接着枚举 \(q\) 中的每个询问,查询区间和,将和记为 \(sum\),两种情况:
-
\(sum \ge k\),说明当前询问的值域一定为 \([l,mid]\)。
-
\(sum < k\),说明当前询问的值域一定为 \([mid+1,r]\)。
注意,每次我们插入树状数组中的均为值域为 \([l,mid]\) 的数,所以若 \(sum < k\),则令 \(k\) 减去 \(sum\),因为下次插入的数中没有值域为 \([l,mid]\) 的数了,所以要将这些数减去。
终止条件即为 \(l=r\),此时记录 \(q\) 序列中所有询问的答案为 \(l\)。
void add(int x,int y) //在树状数组 x 位置加上 y
int query(int x) //查询区间 [1,x] 中的和
void solve(int l,int r,vector<pair<int,int> > a,vector<node> q){
if(l==r){ //更新答案
for(int i=0;i<q.size();i++) ans[q[i].id]=l;
return;
}
vector<pair<int,int> > a1,a2;
vector<node> q1,q2;
int mid=(l+r>>1);
for(int i=0;i<a.size();i++) //插入值域为 [1,mid] 的数
if(a[i].second<=mid) a1.push_back(a[i]),add(a[i].first,1);
else a2.push_back(a[i]); //将 a 分类
for(int i=0;i<q.size();i++){
int sum=query(q[i].r)-query(q[i].l-1);
if(sum>=q[i].k) q1.push_back(q[i]);
else q[i].k-=sum,q2.push_back(q[i]); //将 q 分类
}
for(int i=0;i<a.size();i++)
if(a[i].second<=mid) add(a[i].first,-1); //复原树状数组
solve(l,mid,a1,q1);solve(mid+1,r,a2,q2);
}
时间复杂度分析:据上图(类似线段树的图),发现每一层树均对 \(a,q\) 两个序列操作了 \(n\) 次,由于树高为 \(\log n\),然后加上树状数组的 \(\log n\),总时间复杂度为 \(O(n \log^2 n)\)。
例题 \(2\) 动态区间第 \(k\) 小
给定 \(q\) 次操作,每次操作分为两类:
-
修改 \(a_x\) 为 \(y\)。
-
查询区间 \([l,r]\) 第 \(k\) 小的数。
新增了一个修改操作,但发现修改操作的影响只与 \(a_x\) 和 \(y\),假如当前答案值域为 \([l,r]\),若 \(mid+1 \le a_x,y \le r\),则该修改操作对答案值域为 \([l,mid]\) 的询问毫无影响。但是若 \(l \le a_x \le mid,mid+1 \le y \le r\),此时该把此操作归为哪里呢?
为了避免这种情况的发生,可以将修改操作变为删除操作与加点操作,即为删除 \(a_x\),与在 \(x\) 的位置上加入 \(y\)。这样就只有一个影响因素了。
可能有读者会疑惑,将 \(q\) 重新分类后是否会导致原先的一组询问在修改前,但分类后变为了修改后;或原本为先删除再加点,分类后变为了先加点后删除,这样是否会导致答案不一致?若该修改不影响该询问,那此时先后顺序并无影响;若该操作影响该询问,那在分类的时候是从前向后遍历的,加入新操作也是从前向后加入的,并不会改变互相影响的操作的先后顺序。
此时发现每次递归都传两个 \(vector\) 实在是有点慢,既然顺序不相互影响,那是不是可以直接在原数组上修改。即分类的时候开一个临时数组,最后在原数组上修改,这样可以避免传参的问题。同时为了方便,直接将原数组变为 \(n\) 次加点操作,这样就不用维护 \(a\) 中的数了,只需要维护操作左右边界即可。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define INT_MAX (int)(1e18)
#define mid (l+r>>1)
const int N=3e5+10;
int n,Q,cnt;
int a[N],tr[N],ans[N];
struct node{
int op,x,y,k,id;
//op=0 为询问 此时为询问区间 [x,y] 第 k 小
//op=1 为修改
//若 k=-1 则为删除 x 位置上的 y
//若 k=1 则为 x 位置上加入 y
//由于直接在原数组上进行更改,所以需要记录原 id
}q1[N],q2[N],q[N];
inline int read(){
int t=0,f=1;
register char c=getchar();
while(c<'0'||c>'9') f=(c=='-')?(-1):(f),c=getchar();
while(c>='0'&&c<='9') t=(t<<3)+(t<<1)+(c^48),c=getchar();
return t*f;
}
int lowbit(int x){return x&-x;}
void add(int x,int y){ //在树状数组 x 位置加上 y
while(x<=n) tr[x]+=y,x+=lowbit(x);
}
int query(int x){ //查询区间 [1,x] 中的和
int sum=0;
while(x){
sum+=tr[x];
x-=lowbit(x);
}
return sum;
}
void solve(int l,int r,int L,int R){ //值域为 [l,r] 询问边界为 [L,R]
if(l==r){ //更新答案
for(int i=L;i<=R;i++) if(!q[i].op) ans[q[i].id]=l;
return;
}
int cnt1=0,cnt2=0;
for(int i=L;i<=R;i++){
if(!q[i].op){
int sum=query(q[i].y)-query(q[i].x-1);
if(sum>=q[i].k) q1[++cnt1]=q[i];
else q[i].k-=sum,q2[++cnt2]=q[i]; //分类
}else{
if(q[i].y<=mid) q1[++cnt1]=q[i],add(q[i].x,q[i].k);
else q2[++cnt2]=q[i]; //进行修改操作同时分类
}
}
for(int i=L;i<=R;i++)
if(q[i].op&&q[i].y<=mid)
add(q[i].x,-q[i].k); //复原树状数组
for(int i=1;i<=cnt1;i++) q[L+i-1]=q1[i];
for(int i=1;i<=cnt2;i++) q[L+cnt1+i-1]=q2[i]; //修改原数组
solve(l,mid,L,L+cnt1-1);solve(mid+1,r,L+cnt1,R);
}
signed main(){
cnt=read(),Q=read();
//将初始数组变为加点操作
for(int i=1;i<=cnt;i++)
q[i].op=1,q[i].x=i,q[i].y=read(),q[i].k=1,a[i]=q[i].y;
for(int i=1;i<=Q;i++){
char c;cin>>c;cnt++;
if(c=='Q') q[cnt].op=0;
else q[cnt].op=1;
if(!q[cnt].op) q[cnt].x=read(),q[cnt].y=read(),q[cnt].k=read(),q[cnt].id=i;
else{
q[cnt].x=read(),q[cnt].y=a[q[cnt].x],q[cnt].k=-1;cnt++;
q[cnt].op=1,q[cnt].x=q[cnt-1].x,q[cnt].y=read(),q[cnt].k=1;
a[q[cnt].x]=q[cnt].y;//拆分为删除与加点操作
}
}
//离散化
for(int i=1;i<=cnt;i++) if(q[i].op) a[++n]=q[i].y;
sort(a+1,a+1+n);n=unique(a+1,a+1+n)-(a+1);
for(int i=1;i<=cnt;i++)
if(q[i].op) q[i].y=lower_bound(a+1,a+1+n,q[i].y)-a;
solve(1,n,1,cnt);
for(int i=1;i<=Q;i++)
if(ans[i]) cout<<a[ans[i]]<<"\n";
return 0;
}
发现虽然多了一个修改操作,但是时间复杂度与静态相同,均为 \(n \log^2 n\)。
静态区间的优化
静态区间第 \(k\) 小,可持久化权值线段树可以做到 \(O(n \log n)\),那整体二分能否做到单 \(\log\) 呢。
答案是可以的,但是我不会。oi-wiki 上给出了一种优化整体二分求静态区间的方法。
由于需要与值域 \([l,r]\) 相关,每次树状数组都需要清空然后重新载入。为了避免这种冗余操作,可以设置一个分治点 \(pos\),每次 \(solve\) 的将 \(pos\) 移到 \(mid\) 的位置,同时将所有值域在 \([1,pos]\) 的数加入树状数组中。如下图所示:
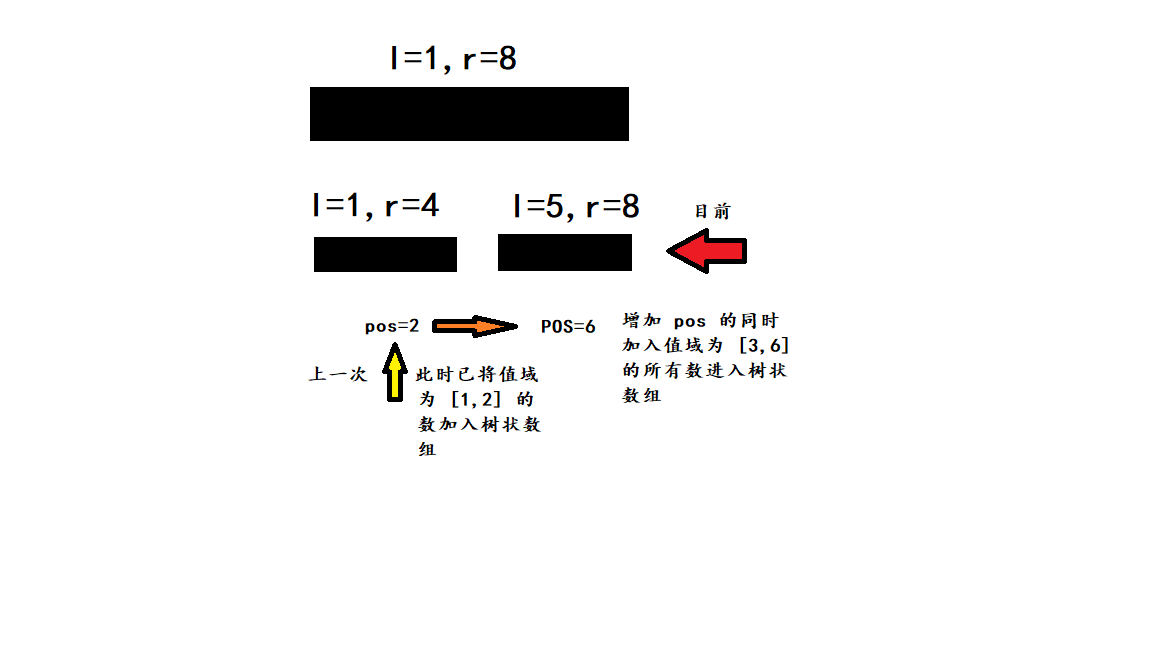
此时就不必再清空树状数组,由于记录的是 \([1,mid]\) 中的所有数,所以分类 \(q\) 的时候,即使 \(sum < k\),也不必使 \(k\) 减去 \(sum\) 了。
可以新建一个
pair<int,int> a[n]
将原数组进行排序,将排序后的原位置与权值记录在 \(b\) 中,方便 \(pos\) 移动的时候加点。
void add(int x,int y) //在树状数组 x 位置加上 y
int query(int x) //查询区间 [1,x] 中的和
void solve(int l,int r,int L,int R){ //分别为答案值域与当前枚举的左右边界
if(l==r){ //更新答案
for(int i=0;i<q.size();i++) ans[q[i].id]=l;
return;
}
int mid=(l+r>>1),cnt1=0,cnt2=0;
while(pos+1<=n&&a[pos+1].first<=mid)
add(a[pos+1].second,1),pos++; //若 mid >= pos,向后加点
while(pos>=1&&a[pos]>mid)
add(a[pos].second,-1),pos--; //若 mid < pos,向前删点
for(int i=0;i<q.size();i++){
int sum=query(q[i].r)-query(q[i].l-1);
if(sum>=q[i].k) q1[++cnt1]=q[i];
else q2[++cnt2]=q[i]; //将 q 分类,此时不必减去 sum
}
solve(l,mid,a1,q1);solve(mid+1,r,a2,q2);
}
总结
以上是整体二分的简单运用,其余情况有些只需更改一下 \(check\) 的方式即可,一些则可能需要更为复杂的变换,应据题分析。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号