BN、CBN、FRN+TUR
1. 归一化 和 BN
神经网络学习过程的本质就是为了学习数据分布,如果我们没有做归一化处理,那么每一批次训练数据的分布不一样,从大的方向上看,神经网络则需要在这多个分布中找到平衡点,从小的方向上看,由于每层网络输入数据分布在不断变化,这也会导致每层网络在找平衡点,显然,神经网络就很难收敛了。当然,如果我们只是对输入的数据进行归一化处理(比如将输入的图像除以255,将其归到0到1之间),只能保证输入层数据分布是一样的,并不能保证每层网络输入数据分布是一样的,所以也需要在神经网络的中间层加入归一化处理。
归一化是计算数据的方差和均值够,将原始数据变换在(0,1)区间内
神经网络中的 BN 不同于一般的归一化操作,是一个有参数、可学习的网络层
假设输入维度是(N,C,H,W),不管哪一层使用什么归一化手段,都不会改变输出大小,即输出维度也是(N,C,H,W)
2. BN
Batch Normalization: 对每一批数据进行归一化。
对于训练中某一个batch的数据{x1,x2,...,xn},注意这个数据是可以输入也可以是网络中间的某一层输出。
BN——神经网络中的位置
某一批次的张量通过卷积层并加上偏置后,relu激活之前,即

BN——步骤和原理
BN步骤主要分为4步:
- 求每一个训练批次数据的均值
- 求每一个训练批次数据的方差
- 使用求得的均值和方差对该批次的训练数据做归一化,获得0-1分布。其中 𝜀 是为了避免除数为 0 时所使用的微小正数。
- 尺度变换和偏移:将 𝑥𝑖 乘以 𝛾 调整数值大小,再加上𝛽增加偏移后得到 𝑦𝑖,这里的 𝛾 是尺度因子,𝛽 是平移因子。这一步是BN的精髓,由于归一化后的 𝑥𝑖 基本会被限制在正态分布下,使得网络的表达能力下降。为解决该问题,我们引入两个新的参数:𝛾,𝛽。 𝛾 和 𝛽 是在训练时网络自己学习得到的。
Batch Normalization网络层的前向传导过程公式就是:
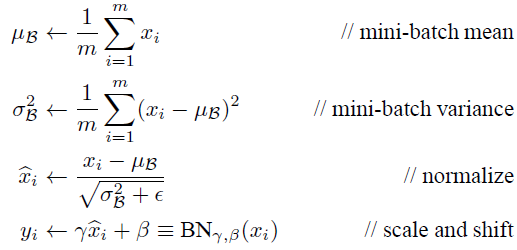
代码形式就是:
m = K.mean(X, axis=-1, keepdims=True)#计算均值
std = K.std(X, axis=-1, keepdims=True)#计算标准差
X_normed = (X - m) / (std + self.epsilon)#归一化
out = self.gamma * X_normed + self.beta#重构变换
关于最后一个公式,及γ、β的解释如下:
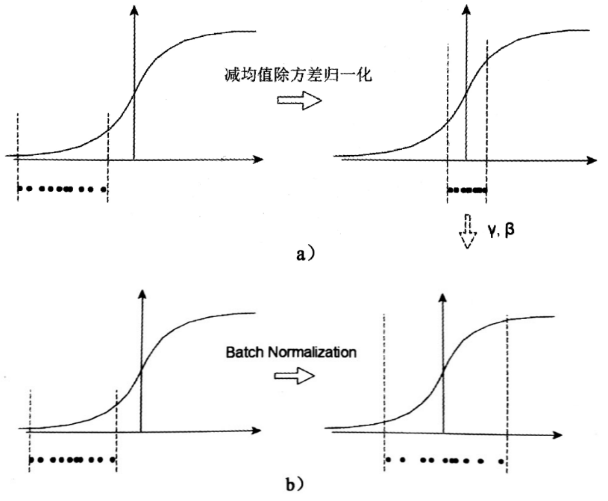
a中左图是没有经过任何处理的输入数据,曲线是sigmoid函数,如果数据在梯度很小的区域,那么学习率就会很慢甚至陷入长时间的停滞。减均值除方差后,数据就被移到中心区域如右图所示,对于大多数激活函数而言,这个区域的梯度都是最大的或者是有梯度的(比如ReLU),这可以看做是一种对抗梯度消失的有效手段。对于一层如此,如果对于每一层数据都那么做的话,数据的分布总是在随着变化敏感的区域,相当于不用考虑数据分布变化了,这样训练起来更有效率。
那么为什么要有第4步,不是仅使用减均值除方差操作就能获得目的效果吗?思考一个问题,减均值除方差得到的分布是正态分布,我们能否认为正态分布就是最好或最能体现我们训练样本的特征分布呢?不能,比如数据本身就很不对称,或者激活函数未必是对方差为1的数据最好的效果,比如Sigmoid激活函数,在-1~1之间的梯度变化不大,那么非线性变换的作用就不能很好的体现,换言之就是,减均值除方差操作后可能会削弱网络的性能!针对该情况,在前面三步之后加入第4步完成真正的batch normalization。
BN的本质就是利用优化变一下方差大小和均值位置,使得新的分布更切合数据的真实分布,保证模型的非线性表达能力。BN的极端的情况就是这两个参数等于mini-batch的均值和方差,那么经过batch normalization之后的数据和输入完全一样,当然一般的情况是不同的。
BN——多维数据中的计算方法
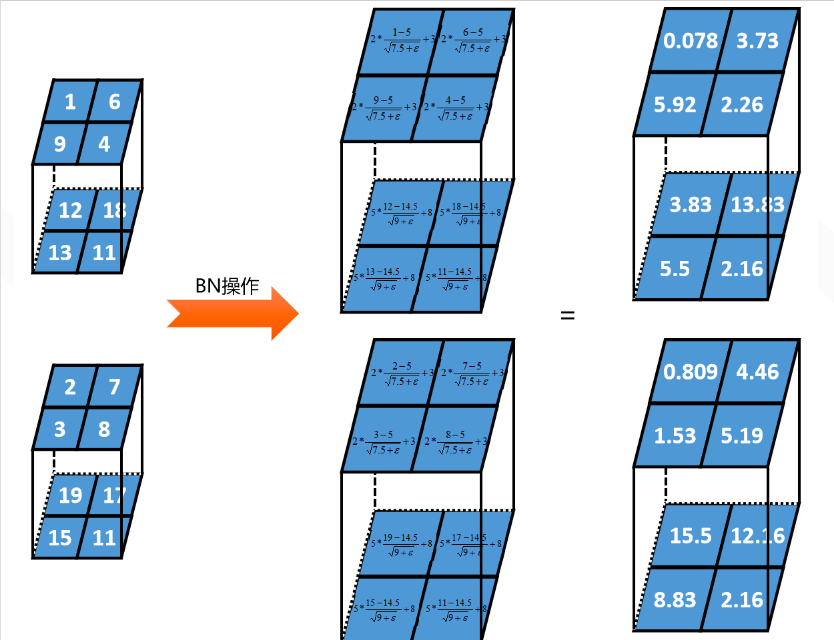
假设某一批次的数据为2个2行2列2深度的张量,BN的过程如下:
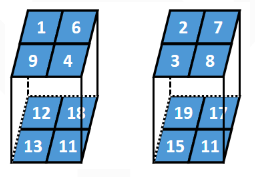
第一步:
计算每一层深度的均值和方差
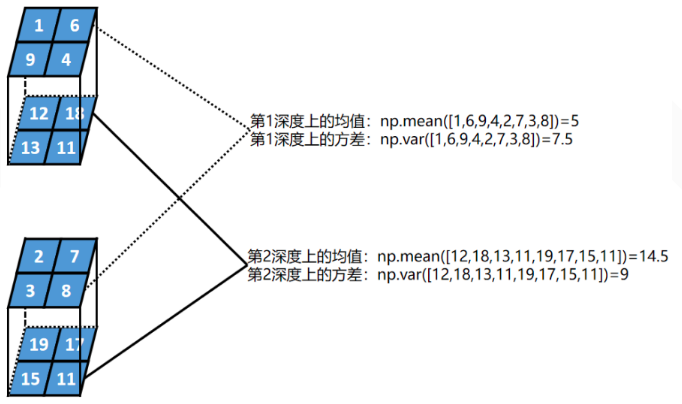
第二步:
对每一层设置2个参数,γ和β。假设第1深度 γ=2、β=3;第2深度 γ=5、β=8。
计算公式:

BN——预测时如何得到均值和方差 ?
预测时,均值和方差是不知道的,而 γ 和 β 是已经通过网络训练出来的。
比如我们预测单个样本时,那还怎么求均值和方法呀!其实是这种样子的,对于预测阶段时所使用的均值和方差,其实也是来源于训练集。比如我们在模型训练时我们就记录下每个batch下的均值和方差,待训练完毕后,我们求整个训练样本的均值和方差期望值,作为我们进行预测时进行BN的的均值和方差:
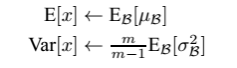
最后测试阶段,BN的使用公式就是:

BN——为什么放在线性层和卷积层之后,而不是非线性层
非线性单元的输出分布形状会在训练过程中变化,归一化无法消除他的方差偏移,相反的,全连接和卷积层的输出一般是一个对称,非稀疏的一个分布,更加类似高斯分布,对他们进行归一化会产生更加稳定的分布。例如像relu这样的激活函数(非线性单元),如果你输入的数据是一个高斯分布,经过他变换出来的数据能是一个什么形状?小于0的被抑制了,也就是分布小于0的部分直接变成0了,这样不是很高斯了,所以不能使用在relu之后使用BN。此外,relu具有防止Gradient Vanish的作用,这和BN的部分作用相同。
BN——作用
1. 防止Gradient Vanish
数据在一些激活函数的梯度很小的区域时,那么学习率就会很慢甚至陷入长时间的停滞。
BN 会调整数据分布,改变均值和方差的位置,从而进入到激活函数梯度最大或较大的区域,从而避免了 Grdient Vanish
以 sigmoid 为例:
如果使用sigmod激活函数的时候,如果不用BN的话,会让反向传播的过程中梯度消失(当输出值较大或较小时,sigmod函数就会进入饱和区域,导致其导数几乎为零),但是可以通过使用Relu激活函数来解决,那就意味着BN主要还是发挥第二个作用——让数据分布变为一致。
2. 防止梯度爆炸
3. 加快收敛速度
允许更大的学习率
BN 层通过将数据改变到合适的位置,对于训练数据、测试数据、和一些样本数很少或几乎没出现过的数据,都能很好的用同一网络得到输出,无需应对特殊数据样本造成的神经网络的较大改动,从而加快神经网络的收敛速度
4. 一定程度的过拟合
在网络的训练中,BN的使用使得一个minibatch中所有样本都被关联在了一起,因此网络不会从某一个训练样本中生成确定的结果,即同样一个样本的输出不再仅仅取决于样本的本身,也取决于跟这个样本同属一个batch的其他样本,而每次网络都是随机取batch,这样就会使得整个网络不会朝这一个方向使劲学习。一定程度上避免了过拟合。
该点也会令,若使用了BN,可以一定程度上减少使用 Dropout 和 Regulation, 因为BN能一定程度提高网络的泛化能力。
BN——不足之处
1. batch size较小时,效果差
BN的过程,是使用batch中样本的均值和方差来模拟全部数据的均值和方差.
在batch_size 较小的时候,模拟出来的肯定效果不好,所以,如果网络中加入了BN,batch_size最好调参的时候调大点。
2. BN 在 RNN 中效果比较差
3. 测试集的均值和方差和训练集差别较大
2,3点参考: https://zhuanlan.zhihu.com/p/152288153
3. BN、LN、IN、GN
BN、LN、IN和GN这四个归一化的计算流程几乎是一样的,可以分为四步:
1.计算出均值
2.计算出方差
3.归一化处理到均值为0,方差为1
4.变化重构,恢复出这一层网络所要学到的分布
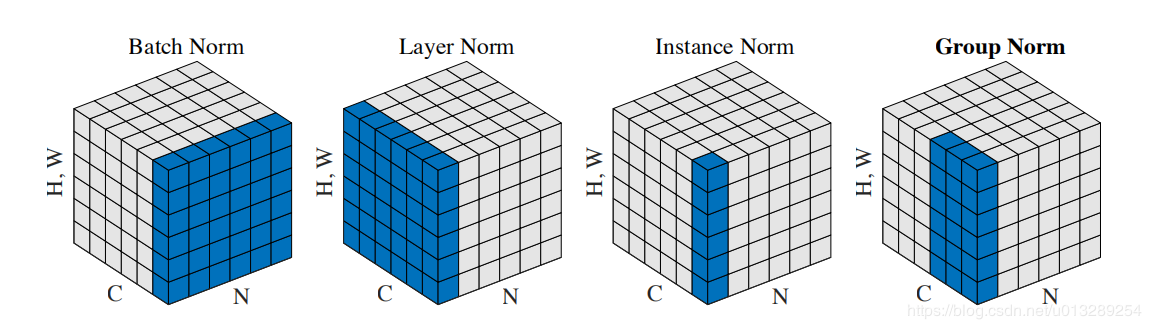
BN
Batch Normalization:
1.BN的计算就是把每个通道的 NHW 单独拿出来归一化处理 (N:batch H:height W:width)
2.可学习权重的维度是(C,),将每个channel看做一个神经元,需要训练的参数数量为: 2C ( 𝛾,𝛽 各有C个)
3.当batch size越小,BN的表现效果也越不好,因为计算过程中所得到的均值和方差不能代表全局
LN
Layer Normalizaiton:
1.LN的计算就是把每个 CHW 单独拿出来归一化处理,不受batch size 的影响 (C:channel H:height W:width)
2.可学习权重的维度是(N,),将每个batch size看做一个神经元,需要训练的参数数量为: 2N ( 𝛾,𝛽 各有N个)
3.常用在RNN网络,但如果输入的特征区别很大,那么就不建议使用它做归一化处理
IN
Instance Normalization
1.IN的计算就是把每个HW单独拿出来归一化处理,不受通道和batchsize 的影响
2.可学习权重的维度是(C,N,),一共 CN 个神经元,需要训练的参数数量为: 2(NC) ( 𝛾,𝛽 各有N*C个)
3.常用在风格化迁移,但如果特征图可以用到通道之间的相关性,那么就不建议使用它做归一化处理
GN
Group Normalizatio
1.GN的计算就是把先把通道C分成G组,然后把每个 GHW 单独拿出来归一化处理,最后把G组归一化之后的数据合并成 CHW
2.GN介于LN和IN之间,当然可以说LN和IN就是GN的特列,比如G的大小为1或者为C
SN
Switchable Normalization
1.将 BN、LN、IN 结合,赋予权重,让网络自己去学习归一化层应该使用什么方法
2.可操作性强,但训练复杂
FRN+TLU
谷歌的提出的FRN层包括归一化层FRN(Filter Response Normalization)和激活层TLU(Thresholded Linear Unit)。FRN层不仅消除了模型训练过程中对batch的依赖,而且当batch size较大时性能优于 BN。
FRN结合归一化和激活函数的方式,替代其他的归一化与激活函数的结合,在各个batch size上的表现都更好
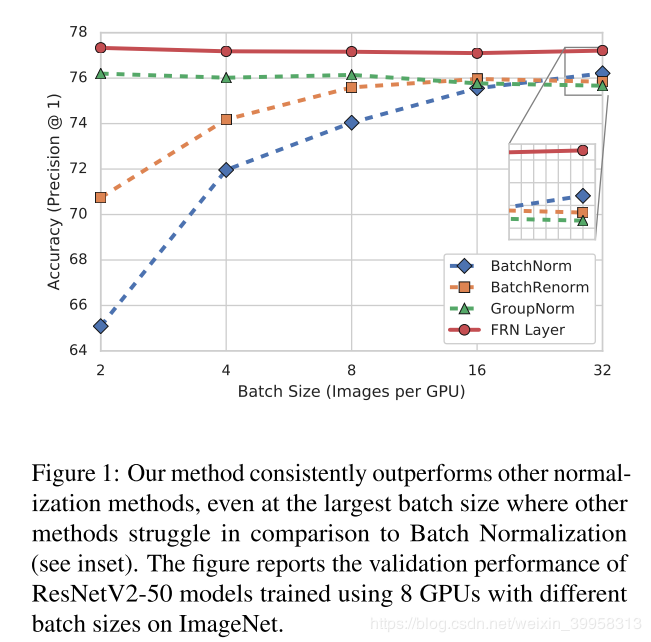
FPN 原理图如下:
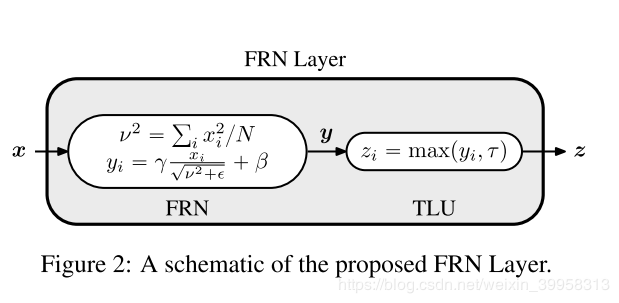


总结: BN目前依然是最常用的归一化方法,GN虽然不会受batch size的影响,但是目前还没大范围采用,不知道FRN的提出会不会替代BN,这需要时间的检验。
CBN——公式复杂,尚未推导,只了解了大致思路
CBN: Cross-Iteration Batch Normalizartion——还是为了解决BN在小batchsize时效果不好的问题
论文作者的思路:
(1) 连续几次训练iteration中模型参数的变化是平滑的
(2) 将前几次iteration的BN参数保存起来,当前iteration的BN参数由当前batch数据求出的BN参数和保存的前几次的 BN 参数共同推算得出(顾名思义 Cross-Interation BN)
(3) 训练前期 BN 参数记忆长度短一些,后期训练稳定了可以保存更长时间的BN参数来参与推算,效果更好
虽然一次的batch size较小,但增加了记忆系统后的batch size可以认为达到了大 batch size的要求
CBN保存的前几次batch的参数是什么??
原理图如下

CmBN——yolov4提出的 CBN 的改进
CBN是对过去的三个batch内的统计参数进行积累
CmBN仅收集单个batch内mini-batch之间的统计数据
其他原理基本相同,都是为了解决batch size较小的问题
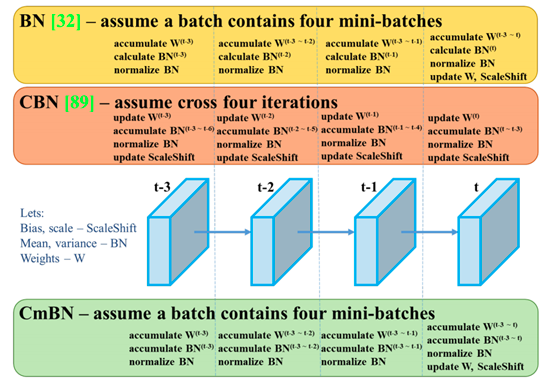
BN、CBN、CmBN对比如下:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号