网络流
网络流
一、基本概念
1、流
A、网络流问题
给定指定的一个有向图,其中有两个特殊的点:源S,汇T。
每条边有指定的容量,求满足条件的从S到T的最大流。
通俗解释:汇T为你家,源S为自来水厂,边即自来水厂和你家之间修的水管子,容量即水管子容量,有的大有的小。自来水厂开闸放水,问你家收到的水最大流量是多少。
B、三个基本的性质:
a、容量限制
如果\(C\)代表每条边的容量,\(F\)代表每条边的流量,那么一定有\(F ≤ C\)
不然水管就爆了。
b、流量守恒
任意一个节点流入量总是等于流出的量,但源和汇不用满足流量守恒。
否则就会蓄水(爆炸警告!)或者平白无故多出水(无 中 生 有)
源无流入,汇无流出。
c、斜对称性
\(x\)向\(y\)的流量为\(F\),那么\(y\)向\(x\)的流量为\(-F\)。
2、网络
网络就是有源汇的有向图,关于什么就是指边权的含义是什么。
A、容量网络
关于容量的网络。
基本是不改变的(极少数问题需要变动)
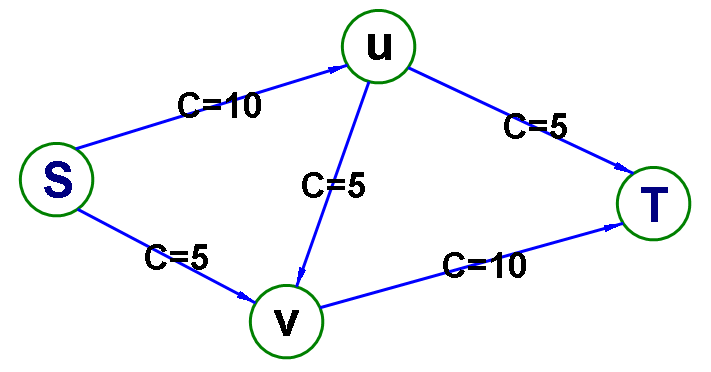
B、流量网络
关于流量的网络。
在求解问题的过程中通常在不断的改变。
总是满足上述三个性质。
调整到最后就是最大流网络,同时也可以得到最大流值
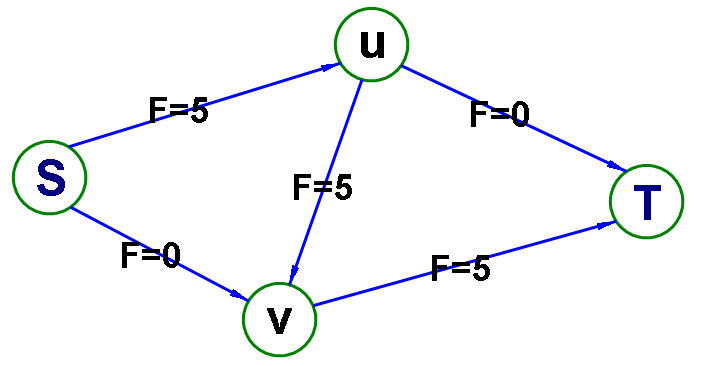
C、残留网络
往往概括了容量网络和流量网络,是最为常用的
残留网络=容量网络-流量网络
这个等式是始终成立的,残留值当流量值为负(斜对称性)时甚至会大于容量值
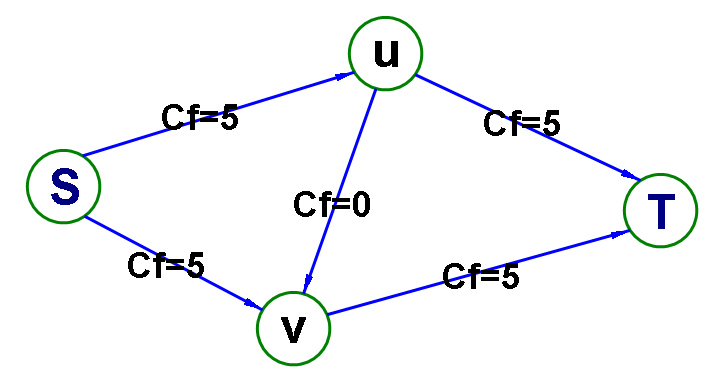
3、割&割集
无向图的割集(Cut Set):C[A,B]是将图G分为A和B两个点集A和B之间的边的全集
网络的割集:C[S,T]是将网络G分为s和t两部分点, S属于s且T属于t,从S到T的边的全集。
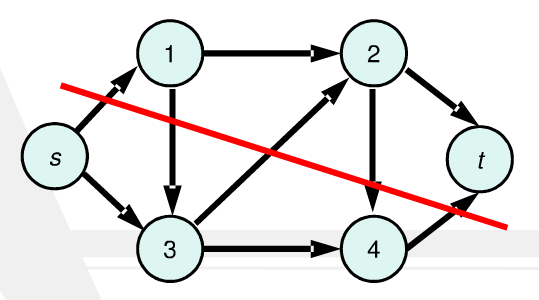
带权图的割(Cut)就是割集中边或者有向边的权和。
通俗的理解一下:
割集好比是一个恐怖分子,把你家和自来水厂之间的水管网络砍断了一些。
然后自来水厂无论怎么放水,水都只能从水管断口哗哗流走了,你家就停水了。
割的大小应该是恐怖分子应该关心的事,毕竟细管子好割一些。
而最小割花的力气最小。
二、最大流最小割定理
网络的最大流等于最小割。
简洁版证明
任意一个流小于等于任意一个割,割和流有且仅有一个重叠值,那么必定有最大流等于最小割。
由于可以构造出一个割等于最大流的割,任何割都大于等于最大流,那么等于最大流的割一定是最小割。
证明
1.任意一个流都小于等于任意一个割
这个很好理解,自来水公司随便给你家通点水,构成一个流。
恐怖分子随便砍几刀,砍出一个割。
由于容量限制,每一根的被砍的水管子流出的水流量都小于管子的容量。
每一根被砍的水管的水本来都要到你家的,现在流到外面,加起来得到的流量还是等于原来的流。
管子的容量加起来就是割,所以流小于等于割。
由于上面的流和割都是任意构造的,所以任意一个流小于任意一个割。
2.构造出一个流等于一个割
当达到最大流, 根据增广路定理:残留网络中st到ed已经没有通路了,否则还能继续增广。
我们把s能到的的点集设为S,不能到的点集为T。
构造出一个割集C[S,T] S到T的边必然满流,否则就能继续增广
这些满流边的流量和就是当前的流即最大流。
把这些满流边作为割,就构造出了一个和最大流相等的割。
3.最大流等于最小割
设相等的流和割分别为Fm和Cm
则因为任意一个流小于等于任意一个割
任意F≤Fm=Cm≤任意C。
三、EK算法(计算最大流)O(VE2)
\(EK\)算法:最短路径增广算法。
\(EK\)算法基于\(FF\)方法,即增广路方法。
1、前置知识:FF方法
增广路方法是很多网络流算法的基础,一般都在残留网络中实现。
A、定义
增广路:即一条st到ed的路径,且路径上的每条边的残留容量都为正。
B、思路
a、找出一条从源到汇的能够增加流的路径
b、调整流值和残留网络
c、重复ab操作,直至没有增广路为止。
C、实现
\(a:\)将残留容量为正的边设为可行的边,\(BFS\)得到增广路。
\(b:BFS\)得到增广路后,增广路能够增广的流值为路径上最小残留容量\(x\)。整张图的最大流值\(Flow+=x\),路径上的边的残留容量\(V-=x\),路径上的反向边的残留容量\(V'+=x\)。
(保证斜对称性。增广好比自来水公司往这条线路里通水,通水的流量就是\(x\),那么流量网络上,正向边就会变大,反向边就会变小,又因残留网络=容量网络-流量网络,所以残留网络上正向边变小,反向边增大。)
2、EK算法的实现
\(EK\)算法在\(FF\)方法的实现过程中,多了一项限制条件,即:BFS得到边数最短的增广路。
(得到边数最短的增广路可以有效减少使用反悔机制的次数,反悔机制将在疑难点中解释)
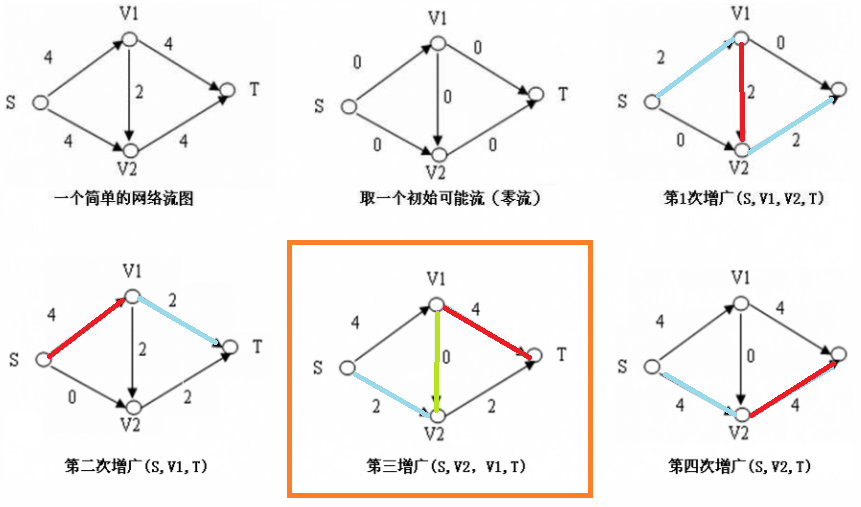
3、疑难点:反向路问题
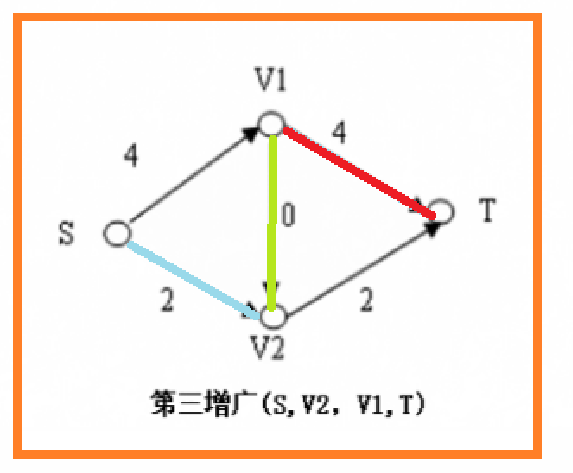
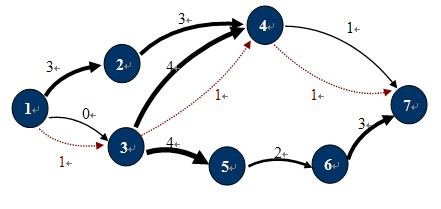
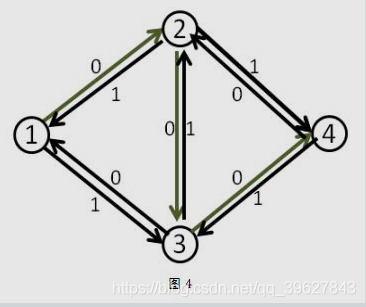
其中绿色的边是走了反路,那么为什么要走反路,为什么可以走反路呢?
假定一个容量网络如下图:

那么第一次增广(路径:\(1->2->3->4\))后:
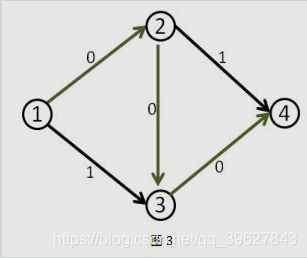
那么此时就已经找不到增广路了,得到的\(Flow=1\)。但显然,如果走\(1->2->4\)和\(1->3->4\)两条路,可以得到更大的\(Flow=2\)。
那么,为了解决这种情况,我们设定了一个反悔机制,即退流,即将自来水厂往这个管子里灌的水全部退回去。而反悔机制的关键,就是反向边。
第一次增广后,整个网络的容量如下:
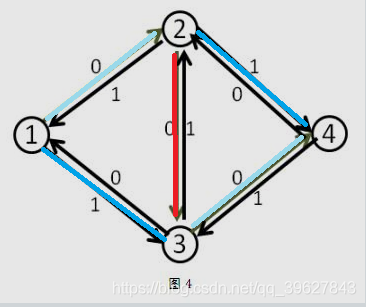
那么,我们可以通过反向边找到一条新的增广路,即\(1->3->2->4\),由于其中\(3->2\)是反向边,即退流,将原本流入这个水管的水退回去流向其他水管,再用别的水管接上这个水管流向的水管。
A、连接问题
因为反向边值为正,那么之前一定有一条增广路走过这条边,即这条边两端都是有边相连的,如图中红色为反向边对应的正边,天蓝色为原本与反向边相连的边。在用新的增广路更新的时候,深蓝色的边将分别接替红边的出口和入口,反向边将正边删除,形成使\(Flow\)更大的新网络。
B、更新问题
a.合法性
因为反向边的容量为正向边流过的容量,即所有过正向边的道路上的最小值之和,那么只要本条增广路上流过的水不多于反向边的容量,即不多于原本正向边上流过的容量,就可以使接替后水管仍旧不会炸裂,即整个网络依旧合法。
而我们每次增广的值都是增广路上边的最小权值,满足不多于反向边的条件,所以整个网络依旧合法。
b.Flow的更新
那么为什么新的增广路可以直接更新Flow的值呢?
因为一条新的增广路相当于从自来水厂多接了一根管子(为了便于理解,有重合边的不同增广路也看作不同的管子),然后哗啦啦往外流水,于是整个自来水厂流出去的水的总值当然就直接加上这条管子流出去的水的值了。
4、代码实现
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=205,M=1e4+5;
int n,m,st,ed,te=1;
int cb[N][N],pre[N],tail[N];
ll D[N],Flow;
struct e_
{
int u,v,pre;ll w;
}e[M];
inline void add(int u,int v,int w)
{
e[++te]=(e_){u,v,tail[u],(ll)w};cb[u][v]=te;tail[u]=te;
}
bool bfs()
{
memset(D,0x3f,sizeof(D));
D[st]--;
vector<int>q;
q.push_back(st);
int l=0;
while(l<q.size())
{
int u=q[l++];
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v;ll w=e[i].w;
if(w<=0||D[v]!=D[0]) continue;
pre[v]=i;
D[v]=min(D[u],w);
q.push_back(v);
if(v==ed) return 1;
}
}
return 0;
}
void update()
{
int p=ed;ll val=D[ed];Flow+=val;
while(pre[p]) e[pre[p]].w-=val,e[pre[p]^1].w+=val,p=e[pre[p]].u;
}
int main()
{
scanf("%d %d %d %d",&n,&m,&st,&ed);
for(int i=1,u,v,w;i<=m;++i)
{
scanf("%d %d %d",&u,&v,&w);
if(cb[u][v]) e[cb[u][v]].w+=(ll)w;
else add(u,v,w),add(v,u,0);
}
while(bfs()) update();
printf("%lld",Flow);
}
四、Dinic算法
\(Dinic\)算法比\(EK\)算法更快。
1、前置知识
链:网络中的一个顶点序列,这个序列中前后两个顶点有弧相连。
前向弧:指方向和链一致的弧。
后向弧:方向和链不一致的弧。
2、实现
A、根据原网络的BFS序给每个点分配深度,st深度为0,st所到的所有点深度为1,以此类推。\((BFS\)得\(now、dep)\)
B、进行多次DFS寻找增广路,u能到v的条件是\(uv\)相连且\(dep[v]=dep[u]+1\)。
C、增广路更新
每次DFS到点u时,都是点u可以往下分配的最大值,然后找往下最多可以消耗多少即可。
3、疑难点
步骤B,不过我也不太清楚,就放着了。
4、代码实现
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define INF 0x7fffffffffffffff
const int N=205,M=1e4+5;
int n,m,st,ed,te=1;
int cb[N][N],dep[N],now[N],tail[N];
ll Flow;
struct e_
{
int u,v,pre;ll w;
}e[M];
inline void add(int u,int v,int w)
{
e[++te]=(e_){u,v,tail[u],(ll)w};cb[u][v]=te;tail[u]=te;
}
bool bfs()
{
memset(dep,0,sizeof(dep));
dep[st]=1;now[st]=tail[st];
vector<int>q;
q.push_back(st);
int l=0;
while(l<q.size())
{
int u=q[l++];
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v;ll w=e[i].w;
if(w==0||dep[v]) continue;
dep[v]=dep[u]+1;now[v]=tail[v];q.push_back(v);
if(v==ed) return 1;
}
}
return 0;
}
ll dfs(int u,ll val)
{
if(u==ed) return val;
int &i=now[u];
ll rest=val;
for(i=now[u];i&&rest;i=e[i].pre)
{
int v=e[i].v;ll w=e[i].w;
if(dep[v]==dep[u]+1&&w)
{
ll d=dfs(v,min(rest,w));
if(!d) dep[v]=0;
rest-=d;e[i].w-=d;e[i^1].w+=d;
}
}
return val-rest;
}
int main()
{
scanf("%d %d %d %d",&n,&m,&st,&ed);
for(int i=1,u,v,w;i<=m;++i)
{
scanf("%d %d %d",&u,&v,&w);
if(cb[u][v]) e[cb[u][v]].w+=(ll)w;
else add(u,v,w),add(v,u,0);
}
while(bfs())
{
while(ll d=dfs(st,INF)) Flow+=d;
}
printf("%lld",Flow);
}
5、模板
#include<bits/stdc++.h>
using namespace std;
const int N=105,M=2e4+5,INF=0x3fffffff;
int n,m,st,ed,Flow;
int te=1,v[M],w[M],pre[M],tail[N];
int dep[N],now[N];
inline void add(int U,int V,int W)
{
++te;v[te]=V;w[te]=W;pre[te]=tail[U];tail[U]=te;
}
bool bfs()
{
memset(dep,0,sizeof(dep));
memcpy(now,tail,sizeof(now));
dep[st]=1;
vector<int>q;
int l=0;
q.push_back(st);
while(l<q.size())
{
int u=q[l++];
for(int i=tail[u];i;i=pre[i])
if(w[i]&&!dep[v[i]])
{
dep[v[i]]=dep[u]+1;
q.push_back(v[i]);
if(v[i]==ed) return 1;
}
}
return 0;
}
int dfs(int u,int val)
{
if(u==ed) return val;
int rest=val;
for(int &i=now[u];i&&rest;i=pre[i])
if(w[i]&&dep[v[i]]==dep[u]+1)
{
int d=dfs(v[i],min(rest,w[i]));
if(!d) dep[v[i]]=0;
else las[v[i]]=u,rest-=d,w[i]-=d,w[i^1]+=d;
}
return val-rest;
}
void init()
{
}
void work()
{
while(bfs())
{
while(int d=dfs(st,INF)) Flow+=d;
}
}
int main()
{
init();
work();
printf("%d",Flow);
}
五、技巧
1.化归思想:将一个问题由难化易,由繁化简,由复杂化简单。
2.注意把多源多汇转化为单源单汇即可利用EK算法解决问题。
3.传递边可以建INF,反边必须为0。
4.边有限制就在边上建立权值,点有限制就把点拆成入点和出点,所有连向这个点的边都连在入点上,所有的从这个点连出的边都连在出点上,入点向出点连一条权值为限制的边。
六、网络流建模经典题
1、最大流
SP4063 MPIGS - Sell Pigs
【题目大意】
有 M 个猪圈,每个猪圈里初始时有若干头猪pig[i]。一开始所有猪圈都是关闭的。依次来了 N 个顾客,每个顾客分别会打开指定的几个猪圈,从中买若干头猪。每 个顾客分别都有他能够买的数量的上限。每个顾客走后,他打开的那些猪圈中的 猪,都可以被任意地调换到其它开着的猪圈里,然后所有猪圈重新关上。问总共 最多能卖出多少头猪。(1 <= N <= 100, 1 <= M <= 1000)
有一个顾客之后,对应的猪圈的猪就可以任意调配,就相当于这些水都流到这个管子里堵着,有的可以通过这个管子流出去(卖掉),有的可以通过别的管子流出去,别的管子指和这个对应的猪圈有重叠的管子。假设这个管子是\({1,2,3}\)重叠为1,但经过这个管子之后1中猪也可以由2,3调配过来,所以就相当于直接在2,3拿猪。
设一个s点为源点,一个t点为汇点
每来一个顾客m+i(顾客从m+1开始编号),如果他所拥有钥匙的猪圈还未被打开过,那连一条源点和他 流量为此猪圈的猪的数量\((s,i,pig[i])\)的边
如果他所拥有钥匙的猪圈index被打开过,那连一条前一个打开的人和他 流量为INF的边\((vis[index],i,INF)\)
**每个顾客与汇点连一条流量为此顾客购买力的边\((m+i,t,buy)**\)
#include<bits/stdc++.h>
using namespace std;
const int N=1105,M=11e4+5,INF=0x3fffffff;
int n,m,st,ed,te=1;
int las[N];
int vv[M<<1],pre[M<<1],now[N],dep[N],tail[N];
int Ans,Flow,ww[M<<1];//dinic
inline void add(int u,int v,int w)
{
++te;vv[te]=v;ww[te]=w;pre[te]=tail[u];tail[u]=te;
}
bool bfs()
{
memset(dep,0,sizeof(dep));
dep[st]=1;now[st]=tail[st];
vector<int>q;
q.push_back(st);
int l=0;
while(l<q.size())
{
int u=q[l++];
for(int i=tail[u];i;i=pre[i])
{
int v=vv[i];int w=ww[i];
if(w==0||dep[v]) continue;
dep[v]=dep[u]+1;
now[v]=tail[v];
q.push_back(v);
if(v==ed) return 1;
}
}
return 0;
}
int dfs(int u,int val)
{
if(u==ed) return val;
int &i=now[u];
int rest=val;
for(;i&&rest;i=pre[i])
{
int v=vv[i];int w=ww[i];
if(dep[v]==dep[u]+1&&w)
{
int d=dfs(v,min(rest,w));
if(!d) dep[v]=0;
rest-=d;ww[i]-=d;ww[i^1]+=d;
}
}
return val-rest;
}
int main()
{
scanf("%d %d",&m,&n);
st=0;ed=n+m+1;
for(int i=1,x;i<=m;++i) scanf("%d",&x),las[i]=i,add(st,i,x),add(i,st,0);
for(int i=1,x,y;i<=n;++i)
{
scanf("%d",&x);
for(int j=1;j<=x;++j)
{
scanf("%d",&y);
add(las[y],m+i,INF);add(m+i,las[y],0);las[y]=m+i;
}
scanf("%d",&x);
add(m+i,ed,x);add(ed,m+i,0);
}
while(bfs())
{
while(int d=dfs(st,INF)) Flow+=d;
}
printf("%d",Flow);
}
P2891 Dining
【题目大意】
有 F 种食物和 D 种饮料,每种食物或饮料只能供一头牛享用,且每头牛只享用一 种食物和一种饮料。现在有 N 头牛,每头牛都有自己喜欢的食物种类列表和饮 料种类列表,问最多能使几头牛同时享用到自己喜欢的食物和饮料。( 1 <= F <= 100, 1 <= D <= 100, 1 <= N <= 100)
以往一般都是左边一个点集表示供应并与源相连, 右边一个点集表示需求并与汇相连。现在不同了,供应有两种资源,需求仍只有 一个群体,
根据这个群体与两种资源的联系来看,食物和饮料之间并没有直接联系,而是牛与食物,牛与饮料分别有联系
可以把牛放在两种资源中间,源点与食物相连,饮料与汇点相连,然后牛在中间食物与牛相连 牛与饮料相连(t->食物->牛->饮料->汇点)
但是会出现一只牛吃多种食物多种饮料的情况所以要把牛拆点拆成(牛,牛',1)为了保证只能吃一次,两者之间流量为1。
#include<bits/stdc++.h>
using namespace std;
const int N=505,M=1e5+5,INF=0x3fffffff;
int n,f,d,m,st,ed,te=1;
int vv[M<<1],pre[M<<1],now[N],dep[N],tail[N];
int Ans,Flow,ww[M<<1];
inline void add(int u,int v,int w)
{
++te;vv[te]=v;ww[te]=w;pre[te]=tail[u];tail[u]=te;
}
bool bfs()
{
memset(dep,0,sizeof(dep));
dep[st]=1;now[st]=tail[st];
vector<int>q;
q.push_back(st);
int l=0;
while(l<q.size())
{
int u=q[l++];
for(int i=tail[u];i;i=pre[i])
{
int v=vv[i];int w=ww[i];
if(w==0||dep[v]) continue;
dep[v]=dep[u]+1;
now[v]=tail[v];
q.push_back(v);
if(v==ed) return 1;
}
}
return 0;
}
int dfs(int u,int val)
{
if(u==ed) return val;
int &i=now[u];
int rest=val;
for(;i&&rest;i=pre[i])
{
int v=vv[i];int w=ww[i];
if(dep[v]==dep[u]+1&&w)
{
int d=dfs(v,min(rest,w));
if(!d) dep[v]=0;
rest-=d;ww[i]-=d;ww[i^1]+=d;
}
}
return val-rest;
}
int main()
{
scanf("%d %d %d",&n,&f,&d);
st=0;ed=n*2+f+d+1;
for(int i=1;i<=f;++i) add(st,i,1),add(i,st,0);
for(int i=1;i<=d;++i) add(f+i,ed,1),add(ed,f+i,0);
for(int i=1,F,D,x;i<=n;++i)
{
scanf("%d %d",&F,&D);
add(f+d+i,f+d+n+i,1);
add(f+d+n+i,f+d+i,0);
for(int j=1;j<=F;++j) scanf("%d",&x),add(x,f+d+i,1),add(f+d+i,x,0);
for(int j=1;j<=D;++j) scanf("%d",&x),add(f+d+n+i,f+x,1),add(f+x,f+d+n+i,0);
}
while(bfs())
{
while(int d=dfs(st,INF)) Flow+=d;
}
printf("%d",Flow);
}
JOJ 2453 Candy
【题目大意】
有N颗糖果和M个小孩,老师现在要把这N颗糖分给这M个小孩。每个小孩i对每颗糖j都有一个偏爱度Aij,如果他喜欢这颗糖Aij=2,否则 Aij=1。小孩i觉得高兴当且仅当∑Cij×Aij>=Bi,j=1,2,…,N,若他分得了糖 j,Cij=1否则Cij=0。问能否合理分配这N颗糖,使得每个小孩都觉得高兴。(1<=N<=100,000, 1<=M<=10,0<=Bi<=1,000,000,000)
【思路】
一种最直观的想法就是每颗糖 i 作为一个点并连边(s, i, ?),每个小孩 j 作为一个 点并连边(j, t, Bj)。若小孩 j 喜欢糖果 i 则连边(i, j, 2),否则连边(i, j, 1),然后求一 次最大流看是否等于∑Bj,但是源点和糖之间的流量无法确定,为什么呢?因为一旦选定一条边之后就只能从这条边流而不能再进入其他的出边
假设流量为1,那如果小孩喜欢此糖的话,流量需要为2,所以pass!
假设流量为2,如果小孩不喜欢的话,流量需要为1,且不能再流向其他小孩了,为2的话就不能保证不再流量另一个不喜欢的小孩,所以pass!
现在转换一下思路,由于问的是否所有孩子都能高兴,为了尽量让孩子高兴,所以每颗糖都会分出去,即Cij=1Cij=1
假设有xx个Aij=2Aij=2,其余Aij=1Aij=1,则 ∑Cij×Aij=∑1∗Aij=N+x∑Cij×Aij=∑1∗Aij=N+x,则所有小孩都高兴即为N+x>=∑BN+x>=∑Bj
所以只考虑可以额外提供1点高兴值的糖果和小孩,因为贡献值从2变为1减半了,所以小孩到汇点的流量也需要减半,
(达到快乐就行了 不能让他多吃了糖果 还有其他小孩呢)
这样就只需要判断小孩是不是喜欢这块糖了,如果喜欢的话,就连边流量为1,如果不喜欢的话就不连边,或者流量为0也行
ZOJ 2760 How Many Shortest Path
【题目大意】
给定一个带权有向图 G=(V, E)和源点 s、汇点 t,问 s-t 边不相交最短路最多有几 条。(1 <= N <= 100)
跑最短路,记录所有最短路上的边e,建网络流图,e容量为1,找最大流。
WOJ 1124 Football Coach
【题目大意】
有 N 支球队,互相之间已经进行了一些比赛,还剩下 M 场没有比。现在给出各 支球队目前的总分以及还剩下哪 M 场没有比,问能否合理安排这 M 场比赛的结 果,使得第 N 支球队最后的总分大于其他任何一支球队的总分。已知每场比赛 胜者得 2 分,败者 0 分,平局则各得 1 分。(1 <= N <= 100, 0 <= M <= 1000)
与N比都让N赢,设最终N得分为S,假设球队\(i\)的得分为\(x\),那么球队最多再得\(S-x-1\)分。球队向ed连边为\(S-x-1\)。除去N参与的比赛还有K场,所有比赛向st连边2,向参与比赛的两支球队连传递边。
最后的Flow如果等于\(K*2\),那么就可以满足,输出\(YES\)。小于就输出\(NO\)。
SGU 326 Perspective
【题目大意】
NBA 某小组内有 N 支球队,小组内以及小组间已经进行了若干场比赛。现在给 出这 N 支球队目前胜利的场数、还剩多少场没有比(包括小组内和小组间)以 及小组内任意两支球队之间还剩多少场没有比,问能否合理安排剩下的所有比赛, 使得球队 1 最后成为小组冠军或者并列冠军。 (2 <= N <= 20, 0 <= x <= 10000, x 表示其他任何输入)
同理,N都赢,球队向ed连\(S-x\)边(因为可以并列),比赛向st连边1,向参加比赛的两支球队连传递边。成立条件为\(Flow=K\)。
SPOJ 287 Smart Network Administrator
【题目大意】
一座村庄有 N 户人家。只有第一家可以连上互联网,其他人家要想上网必须拉 一根缆线通过若干条街道连到第一家。每一根完整的缆线只能有一种颜色。网管 有一个要求,各条街道内不同人家的缆线必须不同色,且总的不同颜色种数最小。 求在指定的 K 户人家都能上网的前提下,最小的不同颜色种数。(1 <= N <= 500)
以第一家作为汇点 t,K 户人家中的每一户 i 作为一个点并连边(s,i,1)(s,i,1),对每条街道(u,v)(u,v),连边(u,v,c),(v,u,c),c=∞(u,v,c),(v,u,c),c=∞。 这样求完最大流后每一条 s-t 流均对应一户人家的缆线,而各条街道内的流量表 示有多少户人家的缆线同时穿过该街道,那么这个流量就是只考虑该条街道的时候最少的不同颜色种数。那么答案是否就是所有街道的不同颜色种数的最大值呢? 当然不是!最大流只保证总流量最大,而不会去管每条流具体该往哪儿流,所以 这么做不一定能得到最优解。我们只要稍微修改这个模型就一定能保证得到最优 解:去对c进行二分,强制 c 等于某个值 limit,再对网络求最大流,如果等于 K,说明用 c 种不同 的颜色已经足够了;如果小于 K,说明 c 种还不够,还需要往高了调。同时此处 的单调性也很明显:c 越高越容易满足要求。
简单来讲,就是在边上加一个权值,为这条边最多可调用的次数。
二分+网络流
SPOJ 962 Intergalactic Map
【题目大意】
在一个无向图中,一个人要从 1 点赶往 2 点,之后再赶往 3 点,且要求中途不能多次经过同一个点。问是否存在这样的路线。(3 <= N <= 30011, 1 <= M <= 50011)
题意转换:找2到1的路和2到3的路,要求两条路没有重叠。
每个点只能用一次,所有每个点拆成入点和出点。st向2的出点(2可以用很多次)连传递边。1,3的出点向ed连权值为1的边。其余的所有边\((u,v)\),都连两条传递边边(设\(u\)为入点,\(u'\)为出点):\((u',v)\),\((v',u)\)。
2、最小割
最大权闭合子图类型题
简单来讲,就是一堆A点一堆B点,选某个A点的前提是选了B中的某些点,选A点可以得到报酬,选B点需要付出代价,问可以得到的最大利润是多少。(报酬和-代价和)
A向st连报酬边,B向ed连代价边,AB间连传递边,Ans=报酬和-最小割。
如果比较闲的话,可以看看另一篇文档里的证明过程
例题
HOJ 2634 How to earn more
【题目大意】
有 M 个项目和 N 个员工。做项目 i 可以获得 Ai 元,但是必须雇用若干个指定的 员工。雇用员工 j 需要花费 Bj 元,且一旦雇用,员工 j 可以参加多个项目的开发。 问经过合理的项目取舍,最多能挣多少钱。(1 <= M, N <= 100)
最小点权覆盖和最大点权独立集类型题
给出所有边,点有点权。
最小点权覆盖:求取出一些点,使每条边至少有一个点被取出,求这些点权值和最小值。
最大点权独立集:求取出一些点,不能有任意一条边的两个点都取到,求这些点权值和最大值。
所有的u在一个集合,所有的v在一个集合,u,v保证不存在交集。
(如果题目中没有保证,可以通过二分图的基本染色操作手动分出u,v集合)
连边:st--u的权值-->u--INF-->v--v的权值-->ed。
割中的边一定是非INF边,将图切成不连通的两份,即将一些点分到对面的集合去,待在原本集合的即位未被取出的点,分到对面的就是已经取出的点。
图中最小割就是最小点权覆盖,所有点的权值和-最小点权覆盖就是最大点权独立集的点权和。
•二分图
定义: 二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
给定一个二分图 G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配。
二分图最小点覆盖和最大独立集都可以转化为最大匹配求解。
在这个基础上,把每个点赋予一个非负的权值,这两个问题就转化为:二分图最小点权覆盖和二分图最大点权独立集。
•最小点权覆盖
定义
从U或者V合中选取一些点,使这些点覆盖所有的边,并且选出来的点的权值尽可能小。
建模
1、先对图二分染色,对于每条边两端点的颜色不同,分成U,V点集
2、然后建立源点S,向其中一种颜色的点连一条容量为该点权值的边
3、建立汇点T,由另一种颜色的点向T连一条容量为该点权值的边
4、对于二分图中原有的边,改为由与S相连的点连向与T相连的点的一条容量为INF的边跑一遍最大流,其结果就是最小点权和。
•最大点权独立集
定义
在二分图中找到权值和最大的点集,使得它们之间两两没有边。(其实它是最小点权覆盖的对偶问题)
建模
先求一次最小点权覆盖集,再用总权值减去它,就得到了最大点权独立集。
即 答案=总权值-最小点覆盖集。
例题
HOJ 2713 Matrix1
【题目大意】
一个 N*M 的网格,每个单元都有一块价值 Cij 的宝石。问最多能取多少价值的宝石且任意两块宝石不相邻。(1 <= N, M <= 50, 0 <= Cij <= 40000)
ZOJ 2532 Internship
有 N 个城市,M 个中转站以及 L 条有向边(u, v, c),表示可以从 u 向 v 传送信息, 带宽为 c。每个城市都在向 CIA 总部发送无穷大的信息量,但是目前总部实际接收带宽已经不能满足要求。CIA 决定要增大某条边的带宽以增大总部的接收带宽, 请找出哪些边带宽的增加能导致总部接收带宽的增加。(1 <= N+M <= 100, 1 <= L <= 1000)
【思路】
\(st\)向所有的城市和中转站连传递边,边按题目中给的连,\(CIA\)为\(ed\)。
相当于给出一个网络,问增加哪些边的容量可以使网络最大流增加。
所以可以先跑一遍最大流得到残留网络,增大其中某些残留为0的边的边权,是可能得到更大流的,我们要找的就是这些边。
这些边满足,一端与st相连,一端与ed相连。
那么就先从ed出发找一遍与哪些点连通,ed出发可以到下一个点的条件是\(!vis[v[i]]\)&&\(w[i]\),要反着走。
然后找一遍st出发有哪些点连通,每个u对于w[i]为0的边都查一下vis[v[i]]是否为0,如果不为0,那么这条边就是我们要找的边,把它加入答案集合。
POJ 1815 Friendship
【题目大意】
现代社会人们都靠电话通信。A 与 B 能通信当且仅当 A 知道 B 的电话号或者 A 知道 C 的电话号且 C 与 B 能通信。若 A 知道 B 的电话号,那么 B 也知道 A 的电 话号。然而不好的事情总是会发生在某些人身上,比如他的电话本丢了,同时他 又换了电话号,导致他跟所有人失去了联系。现在给定 N 个人之间的通信关系 以及特定的两个人 S 和 T,问最少几个人发生不好的事情可以导致 S 与 T 无法通 信并输出这些人。如果无解,输出“NO ANSWER!”。如果存在多组解,输出字典序最小的一组。(2 <= N <= 200)
【思路】
第一个问题很简单啊(都做到现在了这种题就太裸了),少几个人会导致S和T无法通讯,就是最小割嘛。
所有点拆开成入点和出点,边权为1,表示删掉1个人。
其余的边(u,v)连传递边(u',v),(v',u)。
跑一遍最小割就可以得到第一个问题的答案。
如果S,T直接相连,直接输出NO ANSWER!
如果为0,就不用管第二个问题了。
比较麻烦的是第二个问题。(何止是比较麻烦,明明是根本不会)
由于要求最小字典序的,所有从1到n枚举每一个点是否需要割去,由于是从小到大枚举的,所以可以割去时就让他割去,此时字典序最小
何时i可以割去呢?
重新建图使(i,i')之间没有边,然后求最小割,若小于result,其实就是result-1,因为每次枚举的边要么是最小割里的,要么就不是,如果不是result,或者在字典序非最小的割集里就无变化,如果是字典序最小的最小割集里的就result-1,则可以割去。
因为每次都割的字典序最小的边,所以组成的一定是最小割集。
如果一个点可以割去,就直接割掉。
Ural 1277 Cops and Thieves
【题目大意】
一个犯罪团伙打算去偷一家美术馆。警察决定派 K 个人堵住所有从匪窝通向美术 馆的道路不过他们只能驻守在沿途顶点处而不能在匪窝或美术馆,且每个点都有一个需要警察驻守的最低人数 Ri。问警察能否完成任务。(2 < N <= 100, 1 < M <= 10000)
【思路】
指定源点汇点的无向图的带权点连通。
拆点最小割。
条件两种二选一求最小值类型题。
Biologist
有一个长度为n的01串,将第i个位置变为另外一个数字的代价是vi。
有m个要求
每个要求的形式是
首先确定若干位置都要是0或者1
然后给定这K个位置,如果些位置上都满足要求
那么就可以得到Wk元
某些要求如果失败了还要倒着给g元
问最终能够得到的最大利润
输入格式:
第一行是n,m,g
第二行是Vi
接下来m行
第一个数字表示这个集合都要是0还是1
第二个数字Wi表示利润,接下来ki表示这个集合中有k个位置
接下来是这k个位置,
最后还有一个0/1,如果是1,表示如果失败了还要倒着给g元
条件有两种,必须为1或者必须为0,一个点不可能同时满足两个条件,所以就要想办法舍弃其中之一。
如果一开始假定所有条件都满足,那么对于某个点而言,相驳的条件要舍弃其中之一,使最后舍弃的损失最小。
意思就是,满足0的条件,满足1的条件只能二选一,于是想到割的定义里:网络的割集:C[S,T]是将网络G分为s和t两部分点, S属于s且T属于t,从S到T的边的全集。
就相当于把这个点分到s里面或者t里面,如果分到s里面,假设s代表满足0的条件,那么所有让s为0的要求也应该在s里面,于是就可以想到把要求0的条件都放在点靠近s的一边,要求1的条件都放到点的左边。割水管的时候就相当于在舍弃边。
如果一开始为1,那么就与ed相连边权为x,即如果有让这个点为0的条件连过来的时候,x也在路径上最小值候选集中。0时同理。
一个条件,如果是使某个点为0,那么从st与它相连,权值为w+会不会倒贴钱*倒贴的钱,然后与所有他限制的点相连,权值为正无穷,对最小值无影响。(这样只是为了方便修改,如果将正无穷的边换成另外的权值,会导致这个要求亏损的钱可能会超过真正可以亏损的钱。于是调整到了点们都会产生影响的边,原本正无穷的边是只有一个点对他产生影响。)1同理。点门其实只是条件们相连的中转点。
st和ed只是开始和结束的象征,没有特殊意义。
建图为这样:
(让条件不相矛盾的建图)
变0的边连st,变1的边连ed,权值为1,求最小割。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e4+5,M=1e5+5;
const ll INF=0x3fffffff;
int n,m,g,st,ed,te=1;
int a[N],dep[M],vv[M<<1],pre[M<<1],tail[M],now[M];
ll Ans,Flow,ww[M<<1];//dinic
inline void add(int u,int v,int w)
{
++te;vv[te]=v;ww[te]=(ll)w;pre[te]=tail[u];tail[u]=te;
}
bool bfs()
{
memset(dep,0,sizeof(dep));
dep[st]=1;now[st]=tail[st];
vector<int>q;
q.push_back(st);
int l=0;
while(l<q.size())
{
int u=q[l++];
for(int i=tail[u];i;i=pre[i])
{
int v=vv[i];ll w=ww[i];
if(w==0||dep[v]) continue;
dep[v]=dep[u]+1;
now[v]=tail[v];
q.push_back(v);
if(v==ed) return 1;
}
}
return 0;
}
ll dfs(int u,ll val)
{
if(u==ed) return val;
int &i=now[u];
ll rest=val;
for(;i&&rest;i=pre[i])
{
int v=vv[i];ll w=ww[i];
if(dep[v]==dep[u]+1&&w)
{
ll d=dfs(v,min(rest,w));
if(!d) dep[v]=0;
rest-=d;ww[i]-=d;ww[i^1]+=d;
}
}
return val-rest;
}
int main()
{
scanf("%d %d %d",&n,&m,&g);
st=0;
ed=n+m+1;
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=1,x;i<=n;++i)
{
scanf("%d",&x);
if(a[i]) add(i,ed,x),add(ed,i,0);
else add(st,i,x),add(i,st,0);
}
for(int i=1,id,w,k,x;i<=m;++i)
{
scanf("%d %d %d",&id,&w,&k);Ans+=w;
if(id) for(int j=1;j<=k;++j) scanf("%d",&x),add(x,n+i,INF),add(n+i,x,0);
else for(int j=1;j<=k;++j) scanf("%d",&x),add(x,n+i,0),add(n+i,x,INF);
scanf("%d",&x);
if(id) add(n+i,ed,w+x*g),add(ed,n+i,0);
else add(st,n+i,w+x*g),add(n+i,st,0);
}
while(bfs())
{
while(ll d=dfs(st,INF)) Flow+=d;
}
printf("%lld",Ans-Flow);
}
SPOJ 1693 Coconuts
【题目大意】
N 个城堡守卫正在就非洲的燕子能否搬运椰子而进行投票。每个人都有自己的看法,但是为了避免跟自己的朋友持相反意见,他们时常会投相反的票。现在给出每个人的初始看法以及朋友关系,求在某种投票方 案下,违背自己意愿的票数与持不同意见的朋友对数的总和最小。 (2 <= N <= 300, 1 <= M <= N(N-1)/2)
【思路】
解法同上。
朋友关系即此条件要求这些人都选0或1。
hdu 2485 Destroying the bus stations
【题目大意】
给定一个无权有向图 G=(V, E)和源点 s、汇点 t,问最少去掉几个点(连同与其关联的所有边)使得不存在长度小于等于 K 的 s-t 路。(0<N<=50,0<M<=4000,0<K<1000)
【思路】
将长度小于k的s-t路都取出来,建一张点点‘图,求最小割。
如果没有K这个条件,而是只让最短路增大的话,就跟hdu 6852差不多了,都是用根据路径长度对选择出来的路重新构图。有两个地方不同
一个区别是一个有向一个无向。无向的时候在跑最短路就不用区分方向了,这里比6852简化了
另一个区别是一个是最小割,一个是最小割点集。最小割点集需要拆点,这个强化了。
拆点时还是分为入点和出点连边(i,i′,1),其他的新边都是(u+n,v,INF)
加上K这个条件就不是只让最短路增大了,而是增大到(>K),想6852时怎么挑选的边来构图
dij.dis[1][u]+dij.dis[0][v]+w==dij.dis[1][n]
而这里是需要把造成<=K的点去掉,所以就需要把条件改成<=K
dij.dis[1][u]+dij.dis[0][v]+w<=k
还有在构新图的时候不要把边构成无向!
例如:dis[1−>u−>v−>n]<k并且dis[1−>v−>u−>n]<k,只需加u−>v或者u−>v一条边,因为这两个点中割去一个,两条边都会不存在了
如果加成双向边的话,还会有一条存在,就导致错误!
【补充】
hdu上有hack最大流的数据,貌似正解是最小费用最大流,不过我是来练习最大流最小割,所以就不去纠正了
【代码】
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define INF 0x3f3f3f3f
#define mem(a,b) memset(a,b,sizeof(a))
const int maxn=1e5+5;
int n,m,s,t;
struct Edge
{
int v;
int w;
int next;
}G[maxn<<1],e[maxn<<1];
int dhead[maxn],dcnt;
void addEdge(int u,int v,int w)
{
G[++dcnt]={v,w,dhead[u]};
dhead[u]=dcnt;
}
struct Dij
{
int dis[2][maxn];
bool vis[maxn];
priority_queue<pii,vector<pii>,greater<pii> > q;
void dij(int s,int n,bool ok)
{
for(int i=1;i<=n;i++)
dis[ok][i]=INF,vis[i]=0;
dis[ok][s]=0;
q.push({0,s});
while(!q.empty())
{
int u=q.top().second;
q.pop();
if(vis[u])
continue;
vis[u]=1;
for(int i=dhead[u];~i;i=G[i].next)
{
int v=G[i].v;
int w=G[i].w;
if(dis[ok][v] > dis[ok][u]+w)
{
dis[ok][v]=dis[ok][u]+w;
if(!vis[v])
q.push({dis[ok][v],v});
}
}
}
}
}dij;
int head[maxn],cnt;
void add(int u,int v,int w)
{
e[++cnt]={v,w,head[u]};
head[u]=cnt;
e[++cnt]={u,0,head[v]};
head[v]=cnt;
}
struct Dinic
{
int cur[maxn],d[maxn];
bool bfs()
{
queue<int> q;
for(int i=0;i<=2*n+1;i++)
d[i]=-1;
d[s]=0;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=head[u];i!=-1;i=e[i].next)
{
int v=e[i].v;
if(d[v]==-1&&e[i].w>0)
{
d[v]=d[u]+1;
q.push(v);
}
}
}
return d[t]!=-1;
}
int dfs(int u,int flow)
{
int nowflow=0;
if(u==t) return flow;
for(int i=cur[u];i!=-1;i=e[i].next)
{
cur[u]=i;
int v=e[i].v;
if(d[v]==d[u]+1&&e[i].w>0)
{
if(int k=dfs(v,min(flow-nowflow,e[i].w)))
{
e[i].w-=k;
e[i^1].w+=k;
nowflow+=k;
if(nowflow==flow)
break;
}
}
}
if(!nowflow) d[u]=-2;
return nowflow;
}
int din()
{
int ans=0;
while(bfs())
{
for(int i=0;i<=2*n+1;i++)
cur[i]=head[i];
ans+=dfs(s,INF);
}
return ans;
}
}_din;
void Init()
{
mem(dhead,-1);
dcnt=-1;
mem(head,-1);
cnt=-1;
}
int main()
{
int k;
while(~scanf("%d%d%d",&n,&m,&k))
{
Init();
s=1+n,t=n;
if(!(n+m+k))
return 0;
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
addEdge(u,v,1);
addEdge(v,u,1);
}
dij.dij(1,n,true);
dij.dij(n,n,false);
for(int u=1;u<=n;u++)
{
for(int i=dhead[u];~i;i=G[i].next)
{
if(i&1)///只加单向边
continue;
int v=G[i].v;
if(dij.dis[1][u]+dij.dis[0][v]+1<=k)
add(u+n,v,INF);
}
}
for(int i=1;i<=n;i++)
add(i,i+n,1);
int ans=_din.din();
printf("%d\n",ans);
}
}
P6054 [RC-02] 开门大吉
一点多值取一,点之间有制约,求总和最小值。

求最小值就是最小割,把值附在边上,一刀把图切开的最小代价就是最小值。
构造以下图:
- \((i,j)\)向\((i,j+1)\)连权为\(g(i,j)\)的边。
- \((i,j+1\))向\((i,j)\)连\(INF\)边。
- \(st\)向 \((i,1)\)连\(INF\)边。
- \((i,m+1)\)向\(ed\)连\(INF\)边。
- 对于每个限制\((i,j,k)\),从 \((j,p)\)向$ (i,p+k)$连INF边。
![]()
对于删除制约边之前的边,都不可能能让图分为两半。
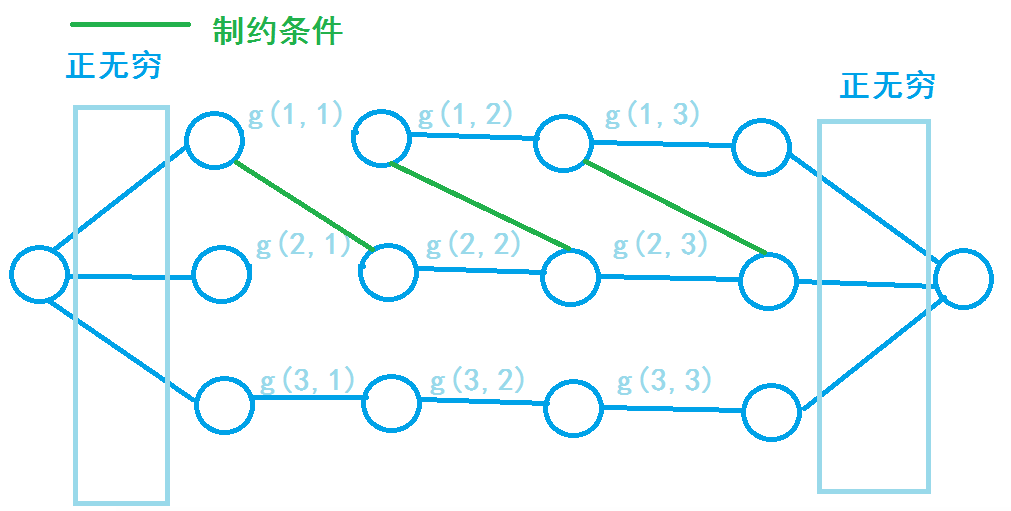
只有删除制约边之后的边,才有可能让图分成两边。
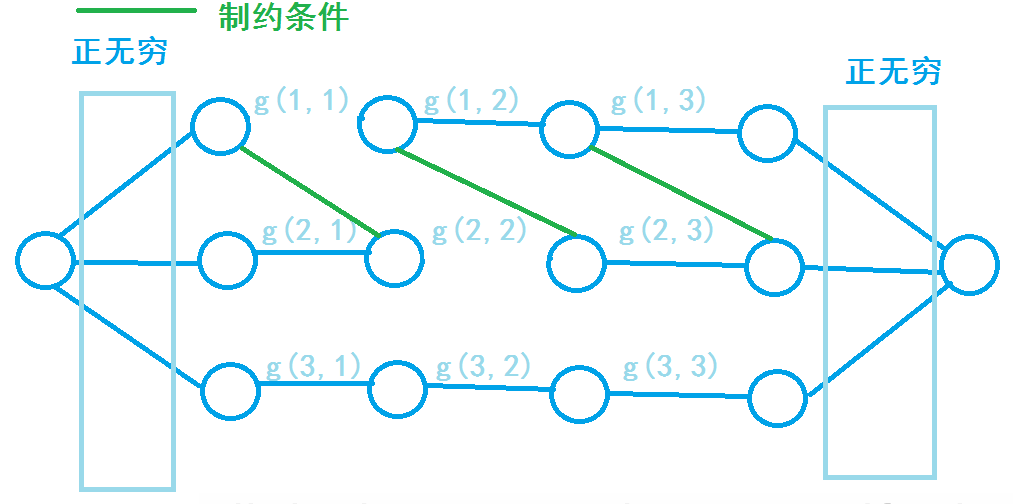
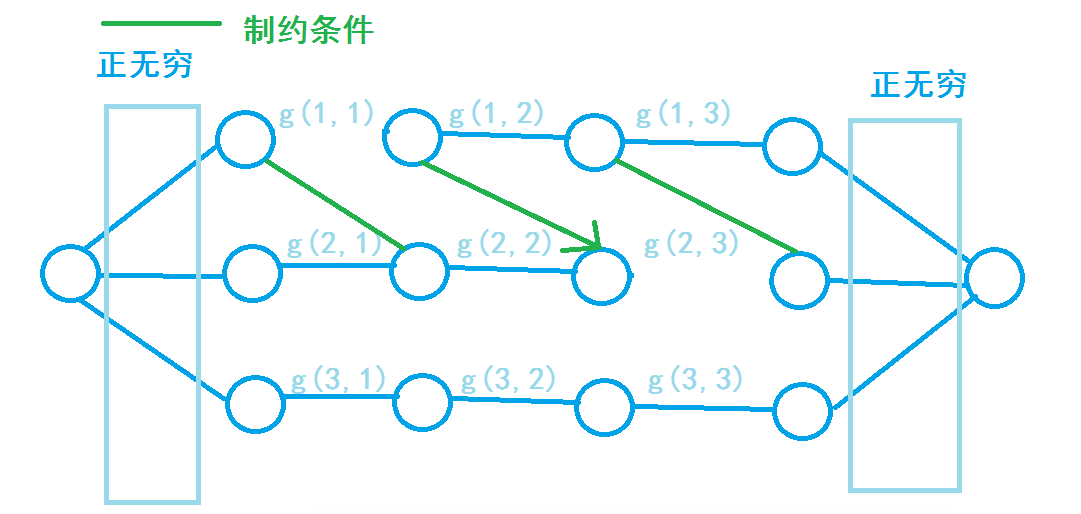
所以这就是通过制约边为什么能完成条件的原理。
3.容量不可为0
预备知识
B(u,v): u->v的流量下界
C(u,v): u->v的流量上界
f(u,v): u->v的流量
可行流只是判断是否可以满足,与最大最小流无关。
无源汇上下界可行流
顾名思义,无源汇上下界可行流:没有源点S,汇点T。在网络中求可行流或者指出不存在。
对于这个问题,不好处理,但是如果我们去掉流量下界限制B,那么就是最大流的模型了,问题就可以解决了。
直接去掉B是不对的。我们规定初始流:每条边先流过B的流量。但是初始流可能会不满足流量平衡。即可能存在:
\(∑(u,i)∈EB(u,i)≠∑(i,v)∈EB(i,v)\)
那么我们加上一个g(附加流)是其满足流量平衡。
\(∑(u,i)∈E[B(u,i)+g(u,i)]=∑(i,v)∈E[B(i,v)+g(i,v)]−−−−−(1)\)
B+g 也就是实际的流量f。
此时我们去掉了流量下界限制B,那么网络中每条边的容量上界限也要减去,已经流过了B的流量,即新网络图中每条边的流量上界限制为C′=C−B,下界限制0。
用最大流求解(求解附加流):
将(1)式移项:
\(∑(u,i)∈EB(u,i)−∑(i,v)∈EB(i,v)=∑(i,v)∈Eg(i,v)−∑(u,i)∈Eg(u,i)\)
令 $M(i)=∑(u,i)∈EB(u,i)−∑(i,v)∈EB(i,v) $
原式:
\(M(i)=∑(i,v)∈Eg(i,v)−∑(u,i)∈Eg(u,i)\)
M(i)是已知的,i点的流入的下界之和减流出的下界之和。
1、如果M(i)≥0
\(∑(i,v)∈Eg(i,v)=∑(u,i)∈Eg(u,i)+M(i)\)
那么我们发现附加流中流出的需要比流入的多M(i)才可以达到流量平衡,那么这些流从哪来呢。建一个源点SS,建一条从SS到i的边,容量为M(i)。
2、如果M(i)≤0
\(∑(i,v)∈Eg(i,v)−M(i)=∑(u,i)∈Eg(u,i)\)
同理,发现附加流中流入的需要比流出的多M(i)才可以达到流量平衡。建一汇点TT,建一条从i到TT点边,容量−M(i),容量也就变成正的了。
建图完毕。从SS到TT跑一遍最大流即可。原图中存在解的条件是:每条从SS连出的边与连向TT的边都需要满流。
注意:只是从SS到TT跑边,SS代表x流入的下限和比流出的下限和多val,判断一下多出来的水能不能流走。
到某个点的流量表示到了这个点,满足完下限后还剩的流量。
TT代表x流入的水比流出的水少val,相当于到了这个点,需要在这个点补充val的流量,于是就把此时的流量,即到了这个点满足完来路的上线后还剩的流量,在这些里拿val出来补充这个点,然后再继续流。
问题:
1、为什么从SS连出的边与连向TT的边满流后才存在解,不满流就不存在解?
SS相当于点x在下界流满后,至少还需要流出去的值。如果流不出去,点x的右边的下限就不能被填满,所以不成立。
TT同理。
2、还有一个小问题,会不会S到i的边未满流,但是另一指向i的边使a流量平衡了。
但是仔细想一下,这是不可能存在的。最大流从S开始跑,整个图中的流量都是从S出发的,而对于S出发的指向i的一条边,它刚好使得i点流量平衡,哪会有多余的流量流给其他点呢?
无源汇上下界网络流到此求解完成。
模板代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5,M=1e6+5;
int n,m,st,ed;
int in[N],out[N],dis[N],now[N];
int te,v[M],w[M],pre[M],tail[N];
inline void add(int U,int V,int up,int low)
{
te++;v[te]=V;w[te]=up-low;pre[te]=tail[U];tail[U]=te;
}
inline bool bfs()
{
memset(dis,0,sizeof(dis));
memcpy(now,tail,sizeof(now));
dis[st]=1;
vector<int>q;
q.push_back(st);
int l=0;
while(l<q.size())
{
int u=q[l++];
for(int i=tail[u];i;i=pre[i])
if(w[i]&&!dis[v[i]])
{
dis[v[i]]=dis[u]+1;
q.push_back(v[i]);
if(v[i]==ed) return 1;
}
}
return 0;
}
int dfs(int u,int val)
{
if(u==ed) return val;
int rest=val;
for(int &i=tail[u];i&&rest;i=pre[i])
if(w[i]&&dis[v[i]]==dis[u]+1)
{
int d=dfs(v[i],min(rest,w[i]));
if(!d) dis[v[i]]=0;
else rest-=d,w[i]-=d,w[i^1]+=d;
}
return val-rest;
}
int main()
{
scanf("%d %d",&n,&m);
st=0;ed=n+1;
for(int i=1,u,v,up,low;i<=m;++i) scanf("%d %d %d",&u,&v,&up,&low),out[u]+=low,in[v]+=low,add(u,v,up-low),add(v,u,0);
for(int i=1;i<=n;++i)
if(in[i]>out[i]) add(st,i,in[i]-out[i]),add(i,st,0);
else add(i,ed,out[i]-in[i]),add(ed,i,0);
while(bfs(st))
{
while(dfs(st,1e9));
}
for(int i=tail[st];i;i=pre[i])
if(w[i])
{
printf("Fail\n");
return 0;
}
for(int i=tail[ed];i;i=pre[i])
if(w[i])
{
printf("Fail\n");
return 0;
}
printf("Success\n");
}
有源汇上下界可行流
有源汇上下界可行流相比有源汇上下界可行流,多了源点S和汇点T,求从S到T满足每条边的流量都满足限制,且除S,T,其他点都满足流量平衡。因为只有S和T不满足流量平衡,所以,如果可以使S,T也满足流量平衡,那么就可以直接套用无源汇上下界可行流了。
那么具体如何操作呢?
源点的性质是只有流出的没有流入的,汇点恰好相反,而且对于源点流出的和汇点流入的,这些流量是相等的。所以建一条从T到S的边容量为INF,那么流入汇点的流量就会从这条边流入S。有源汇到无源汇转换完成,跑一遍从SS到TT的最大流即可。可行流的流量也就是这条边的流量。
模板代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5,M=1e6+5;
int n,m,S,T,st,ed;
int in[N],out[N],dis[N],now[N];
int te,v[M],w[M],pre[M],tail[N];
inline void add(int U,int V,int up,int low)
{
te++;v[te]=V;w[te]=up-low;pre[te]=tail[U];tail[U]=te;
}
inline bool bfs(int x)
{
memset(dis,0,sizeof(dis));
memcpy(now,tail,sizeof(now));
dis[x]=1;
vector<int>q;
q.push_back(x);
int l=0;
while(l<q.size())
{
int u=q[l++];
for(int i=tail[u];i;i=pre[i])
if(w[i]&&!dis[v[i]])
{
dis[v[i]]=dis[u]+1;
q.push_back(v[i]);
if(v[i]==ed) return 1;
}
}
return 0;
}
int dfs(int u,int val)
{
if(u==ed) return val;
int rest=val;
for(int &i=tail[u];i&&rest;i=pre[i])
if(w[i]&&dis[v[i]]==dis[u]+1)
{
int d=dfs(v[i],min(rest,w[i]));
if(!d) dis[v[i]]=0;
else rest-=d,w[i]-=d,w[i^1]+=d;
}
return val-rest;
}
int main()
{
scanf("%d %d %d %d",&n,&m,&S,&T);
st=0;ed=n+1;
for(int i=1,u,v,up,low;i<=m;++i) scanf("%d %d %d",&u,&v,&up,&low),out[u]+=low,in[v]+=low,add(u,v,up-low),add(v,u,0);
for(int i=1;i<=n;++i)
if(in[i]>out[i]) add(st,i,in[i]-out[i]),add(i,st,0);
else add(i,ed,out[i]-in[i]),add(ed,i,0);
add(T,S,1e9);add(S,T,0);
while(bfs(st))
{
while(dfs(st,1e9));
}
for(int i=tail[st];i;i=pre[i])
if(w[i])
{
printf("Fail\n");
return 0;
}
for(int i=tail[ed];i;i=pre[i])
if(w[i])
{
printf("Fail\n");
return 0;
}
printf("Success\n");
}
无源汇上下界可行流到此求解完成。
无源汇上下界可行流没有例题,因为在下面两个中都会用到。
有源汇上下界最大最小流
最大流:残留网络S-->T,把水排出来
最小流:残留网络T-->S,把水压回去
有源汇上下界最大流与有源汇上下界可行流相比,不只是可行流,而且要最大。依然每条边满足容量限制,除源点汇点满足流量平衡。
首先,前提是必须有可行流,所以先套用有源汇上下界可行流来判断是否有解。如果没解就直接输出,有解继续往下看。然后,判断后的残量网络上跑一遍从S到T的最大流,让还有自由流的边多流一些,然后将可行流与这次的最大流相加即可。
为什么这样可以求出最大流?
SS连出的所有边,容量都是流入的下界之和-流出的下界之和,所以当这些边都满流时,说明这些点实际流出的流量=流入的下界之和。那么流入的上界可能并没有达到。对于连向TT的边同样是这样。所以在残余网络上,可能可以继续流一些的,从S到T的最大流,刚好把这些流量全加上。此时再加上可行流,就是最大流。
这样做会不会不满足流量限制了?
在原图中SS,TT的边已经满流了,而且最后的最大流,是不经过这些边的,无法改动这些边的。
代码实现(两种方法):
1、判断可行流,删除T->S的边,求S到T的最大流,answer=可行流+最大流。
2、判断可行流,求S到T的最大流,answer=最大流。仔细一想就明白了,T->S这条边不可能走,而它的反向边S->T容量(可行流)是要走的,所以可行流的流量会从S->T增广到T。
还有一种求解的方法:
在判断可行流时,增加了一条T->S的边,B=0,C = INF。如果存在可行流,那么T->S这条边的容量就是可行流的流量,假设这个流量为a。所以,每次我们可以给a一个值,如果存在解,那么说明这个值是可行的,所以二分a,判断是否可行即可。
无源汇上下界最大流到此求解完成。
例题:loj #116. 有源汇有上下界最大流
有源汇上下界最小流
这个相比上面就是求最小流了。
同样,先判断是否有解。之后求一遍T到S的最大流,用可行减去最大流。考虑反向边的增加量是表示正向边的减少量,所以求出从T到S的最大减少量就是最小流了。
代码实现:判断可行流,删T->S的边,求一遍T到S的最大流,answer=可行流-最大流。
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5,M=1e6+5;
int n,m,S,T,st,ed,Flow;
int in[N],out[N],dis[N],now[N];
int te,v[M],w[M],pre[M],tail[N];
inline void add(int U,int V,int up,int low)
{
te++;v[te]=V;w[te]=up-low;pre[te]=tail[U];tail[U]=te;
}
inline bool bfs()
{
memset(dis,0,sizeof(dis));
memcpy(now,tail,sizeof(now));
dis[st]=1;
vector<int>q;
q.push_back(st);
int l=0;
while(l<q.size())
{
int u=q[l++];
for(int i=tail[u];i;i=pre[i])
if(w[i]&&!dis[v[i]])
{
dis[v[i]]=dis[u]+1;
q.push_back(v[i]);
if(v[i]==ed) return 1;
}
}
return 0;
}
int dfs(int u,int val)
{
if(u==ed) return val;
int rest=val;
for(int &i=tail[u];i&&rest;i=pre[i])
if(w[i]&&dis[v[i]]==dis[u]+1)
{
int d=dfs(v[i],min(rest,w[i]));
if(!d) dis[v[i]]=0;
else rest-=d,w[i]-=d,w[i^1]+=d;
}
return val-rest;
}
int main()
{
scanf("%d %d %d %d",&n,&m,&S,&T);
st=0;ed=n+1;
for(int i=1,u,v,up,low;i<=m;++i) scanf("%d %d %d",&u,&v,&up,&low),out[u]+=low,in[v]+=low,add(u,v,up-low),add(v,u,0);
for(int i=1;i<=n;++i)
if(in[i]>out[i]) add(st,i,in[i]-out[i]),add(i,st,0);
else add(i,ed,out[i]-in[i]),add(ed,i,0);
add(T,S,1e9);add(S,T,0);
while(bfs(st))
{
while(int d=dfs(st,1e9)) Flow+=d;
}
for(int i=tail[st];i;i=pre[i])
if(w[i])
{
printf("Fail\n");
return 0;
}
for(int i=tail[ed];i;i=pre[i])
if(w[i])
{
printf("Fail\n");
return 0;
}
tail[T]=pre[tail[T]];
tail[S]=pre[tail[S]];//删掉多余的边!!!
while(bfs(st))
{
while(int d=dfs(st,1e9)) Flow+=d;
}
printf("Max_Flow=%d\n",Flow);
while(bfs(ed))
{
while(int d=dfs(ed,1e9)) Flow-=d;
}
printf("Min_Flow=%d\n",Flow);
}
4、费用流
MCMF 算法
在最大流的 EK 算法求解最大流的基础上,把 用 BFS 求解任意增广路 改为 用 SPFA 求解单位费用之和最小的增广路 即可。
相当于把\(w(u,v)\)作为边权,在残存网络上求最短路。
类 Dinic 算法
Primal-Dual优化dijkstra
背一下模板就好了啦!
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=5e3+5,M=1e5+5;
int n,m,st,ed;
ll Flow,Cost;
int tail[N],las[N],line[N];
ll flow[N],dis[N],h[N];
int te=1,v[M],pre[M];
ll w[M],f[M];
bool vis[N];
inline void add(int U,int V,int W,int F)
{
++te;
v[te]=V;
w[te]=(ll)W;
f[te]=(ll)F;
pre[te]=tail[U];
tail[U]=te;
}
bool dij()
{
priority_queue<pair<ll,int> >q;
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
memset(las,0,sizeof(las));
memset(line,0,sizeof(line));
flow[st]=0x3fffffff;
dis[st]=0;
q.push({-dis[st],st});
while(!q.empty())
{
int u=q.top().second;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(int i=tail[u];i;i=pre[i])
if(f[i]&&dis[v[i]]>dis[u]+w[i]+h[u]-h[v[i]])
{
las[v[i]]=u;
line[v[i]]=i;
flow[v[i]]=min(f[i],flow[u]);
dis[v[i]]=dis[u]+w[i]+h[u]-h[v[i]];
q.push({-dis[v[i]],v[i]});
}
}
return dis[ed]!=dis[0];
}
void work()
{
while(dij())
{
Flow+=flow[ed];
Cost+=flow[ed]*(dis[ed]-h[st]+h[ed]);
int p=ed;
while(p!=st) f[line[p]]-=flow[ed],f[line[p]^1]+=flow[ed],p=las[p];
for(int i=1;i<=n;++i) h[i]+=dis[i];
}
}
int main()
{
//建边
work();
printf("%lld %lld",Flow,Cost);
}
zkm费用流
#include<bits/stdc++.h>
using namespace std;
const int N=5e3+5,M=1e5+5,INF=1e9;
int n,m,st,ed,Flow,Cost;
int dis[N],tail[N];
int te=1,v[M],w[M],f[M],pre[M];
bool vis[N];
inline void add(int U,int V,int W,int F)
{
++te;
v[te]=V;w[te]=W;f[te]=F;pre[te]=tail[U];
tail[U]=te;
}
bool spfa()
{
for(int i=st;i<=ed;++i) dis[i]=INF,vis[i]=0;
deque<int>q;
dis[ed]=0;
q.push_back(ed);
while(q.size())
{
int u=q.front();
q.pop_front();
vis[u]=0;
for(int i=tail[u];i;i=pre[i])
if(f[i^1]&&dis[v[i]]>dis[u]-w[i])
{
dis[v[i]]=dis[u]-w[i];
if(!vis[v[i]])
{
vis[v[i]]=1;
if(q.empty()||dis[q.front()]<dis[v[i]])q.push_back(v[i]);
else q.push_front(v[i]);
}
}
}
return dis[st]<INF;
}
inline int dfs(int u,int val)
{
vis[u]=1;
if(u==ed)return val;
int rest=val;
for(int i=tail[u];i&&rest;i=pre[i])
if(!vis[v[i]]&&f[i]&&dis[v[i]]+w[i]==dis[u])
{
int d=dfs(v[i],min(f[i],rest));
if(!d) dis[v[i]]=0;
else rest-=d,f[i]-=d,f[i^1]+=d;
}
return val-rest;
}
void init()
{
}
void work()
{
while(spfa())
{
vis[ed]=1;
while(vis[ed])
{
memset(vis,0,sizeof(vis));
int d=dfs(st,INF);
Flow+=d;
Cost+=d*dis[st];
}
}
}
int main()
{
init();
work();
printf("%d %d",Flow,Cost);
}
5、动态开点
首先引入动态开点例题的原身:
P2053 [SCOI2007]修车
给出n辆车m个人,每个人一次可以修一辆车,\(a[i][j]\)为第j个人修第i辆车的时间,问如何安排车的顺序和修的人,使等待的时间最少,输出平均等待时间。
(每辆车的等待时间包括自己被修的时间)
枚举一下,某车是第k个修由j修,花费,即等待时间是\((n-k)*a[i][j]\)。
#include<bits/stdc++.h>
using namespace std;
const int N=5e3+5,M=1e5+5,INF=1e9;
int n,m,st,ed,Flow,Cost;
int dis[N],tail[N];
int te=1,v[M],w[M],f[M],pre[M];
bool vis[N];
inline void add(int U,int V,int W,int F)
{
++te;
v[te]=V;w[te]=W;f[te]=F;pre[te]=tail[U];
tail[U]=te;
}
bool spfa()
{
for(int i=st;i<=ed;++i) dis[i]=INF,vis[i]=0;
deque<int>q;
dis[ed]=0;
q.push_back(ed);
while(q.size())
{
int u=q.front();
q.pop_front();
vis[u]=0;
for(int i=tail[u];i;i=pre[i])
if(f[i^1]&&dis[v[i]]>dis[u]-w[i])
{
dis[v[i]]=dis[u]-w[i];
if(!vis[v[i]])
{
vis[v[i]]=1;
if(q.empty()||dis[q.front()]<dis[v[i]])q.push_back(v[i]);
else q.push_front(v[i]);
}
}
}
return dis[st]<INF;
}
inline int dfs(int u,int val)
{
vis[u]=1;
if(u==ed)return val;
int rest=val;
for(int i=tail[u];i&&rest;i=pre[i])
if(!vis[v[i]]&&f[i]&&dis[v[i]]+w[i]==dis[u])
{
int d=dfs(v[i],min(f[i],rest));
if(!d) dis[v[i]]=0;
else rest-=d,f[i]-=d,f[i^1]+=d;
}
return val-rest;
}
void init()
{
scanf("%d %d",&m,&n);
st=0;ed=(m+1)*n+1;
for(int i=1;i<=n;++i) add(st,i,0,1),add(i,st,0,0);
int x;
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
scanf("%d",&x);
for(int k=1;k<=n;++k)
{
add(i,n*j+k,k*x,1);
add(n*j+k,i,-k*x,0);
}
}
}
int S=n*m+n;
for(int i=n+1;i<=S;++i) add(i,ed,0,1),add(ed,i,0,0);
}
void work()
{
while(spfa())
{
vis[ed]=1;
while(vis[ed])
{
memset(vis,0,sizeof(vis));
int d=dfs(st,INF);
Flow+=d;
Cost+=d*dis[st];
}
}
}
int main()
{
init();
work();
printf("%.2lf",1.0*Cost/n);
}
由本题易得,最先走的增广路一定是第n个修,即\(a[i][j]*1\)的时候。对于每个点,一定会先走\(a[i][j]*k\),k更小的边。
所以可以先加K=1的边,如果增光到了\((j,k)\)的边,就把\((j,k+1)\)的边加入边集。和直接把所有边加进去的做法相比,这样可以有效的减少每次查询的边的数量。
于是给出模板题:
P2050 [NOI2012]美食节
80pts的代码
#include<bits/stdc++.h>
using namespace std;
const int N=100005,M=1e7+5,INF=1e9;
int n,m,st,ed,Flow,Cost;
int dis[N],tail[N];
int te=1,v[M],w[M],f[M],pre[M];
bool vis[N];
int a[50][105],sum,up,b[50],id,cnt[105],num[N];
inline void add(int U,int V,int W,int F)
{
++te;
v[te]=V;w[te]=W;f[te]=F;pre[te]=tail[U];tail[U]=te;
}
inline void add_(int x)
{
num[++id]=x;
cnt[x]++;
add(id,ed,0,1);
add(ed,id,0,0);
for(int i=1;i<=n;++i)
add(i,id,cnt[x]*a[i][x],1),
add(id,i,-cnt[x]*a[i][x],0);
}
int now[N];
bool spfa()
{
for(int i=st;i<=id;++i) now[i]=tail[i],dis[i]=INF,vis[i]=0;
deque<int>q;
dis[ed]=0;
q.push_back(ed);
while(q.size())
{
int u=q.front();
q.pop_front();
vis[u]=0;
for(int i=tail[u];i;i=pre[i])
if(f[i^1]&&dis[v[i]]>dis[u]-w[i])
{
dis[v[i]]=dis[u]-w[i];
if(!vis[v[i]])
{
vis[v[i]]=1;
if(q.empty()||dis[q.front()]<dis[v[i]])q.push_back(v[i]);
else q.push_front(v[i]);
}
}
}
return dis[st]<INF;
}
inline int dfs(int u,int val)
{
if(u==ed)return val;
vis[u]=1;
int rest=val;
for(int &i=now[u];i&&rest;i=pre[i])
if(!vis[v[i]]&&f[i]&&dis[v[i]]+w[i]==dis[u])
{
int d=dfs(v[i],min(f[i],rest));
if(!d) dis[v[i]]=0;
else
{
rest-=d,f[i]-=d,f[i^1]+=d;
if(v[i]==ed) add_(num[u]);
}
}
vis[u]=0;
return val-rest;
}
void init()
{
scanf("%d %d",&n,&m);
st=0;ed=n*m+n+1;
for(int i=1,x;i<=n;++i) scanf("%d",&b[i]),sum+=b[i],up=max(up,b[i]),add(st,i,0,b[i]),add(i,st,0,0);
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
scanf("%d",&a[i][j]);
id=n;
for(int j=1;j<=m;++j)
{
cnt[j]=1,num[++id]=j,
add(id,ed,0,1),add(ed,id,0,0);
for(int i=1;i<=n;++i)
add(i,id,a[i][j],1),add(id,i,-a[i][j],0);
}
}
void work()
{
while(spfa())
{
int d=dfs(st,INF);
for(int i=st;i<=id;++i) vis[i]=0;
Flow+=d;
Cost+=d*dis[st];
}
}
int main()
{
init();
work();
printf("%d",Cost);
}
至此,建模本领应该逐渐成熟了,所以,终极挑战:
网络流二十四题
P2756 飞行员配对方案问题
题目背景
第二次世界大战期间,英国皇家空军从沦陷国征募了大量外籍飞行员。由皇家空军派出的每一架飞机都需要配备在航行技能和语言上能互相配合的两名飞行员,其中一名是英国飞行员,另一名是外籍飞行员。在众多的飞行员中,每一名外籍飞行员都可以与其他若干名英国飞行员很好地配合。
题目描述
一共有 nn 个飞行员,其中有 mm 个外籍飞行员和 (n - m)(n−m) 个英国飞行员,外籍飞行员从 11 到 mm 编号,英国飞行员从 m + 1m+1 到 nn 编号。 对于给定的外籍飞行员与英国飞行员的配合情况,试设计一个算法找出最佳飞行员配对方案,使皇家空军一次能派出最多的飞机。
输入格式
输入的第一行是用空格隔开的两个正整数,分别代表外籍飞行员的个数 mm 和飞行员总数 nn。
从第二行起到倒数第二行,每行有两个整数 u, vu,v,代表外籍飞行员 uu 可以和英国飞行员 vv 配合。
输入的最后一行保证为 -1 -1,代表输入结束。
输出格式
本题存在 Special Judge。
请输出能派出最多的飞机数量,并给出一种可行的方案。
输出的第一行是一个整数,代表一次能派出的最多飞机数量,设这个整数是 kk。
第 22 行到第 k + 1k+1 行,每行输出两个整数 u, vu,v,代表在你给出的方案中,外籍飞行员 uu 和英国飞行员 vv 配合。这 kk 行的 uu 与 vv 应该互不相同。
输入输出样例
输入 #1 复制
5 10
1 7
1 8
2 6
2 9
2 10
3 7
3 8
4 7
4 8
5 10
-1 -1
输出 #1 复制
输出 #1 复制
4
1 7
2 9
3 8
5 10
说明/提示
【数据范围与约定】
说明/提示
【数据范围与约定】
对于 100%100% 的数据,保证 1 \leq m \leq n < 1001≤m≤n<100,1 \leq u \leq m < v \leq n1≤u≤m<v≤n,同一组配对关系只会给出一次。
【提示】
请注意输入的第一行先读入 mm,再读入 nn。
这道题很简单,只是多加了一个las前向数组和判断输出,直接上代码:
#include<bits/stdc++.h>
using namespace std;
const int N=105,M=2e4+5,INF=0x3fffffff;
int n,m,st,ed,Flow;
int te=1,v[M],w[M],pre[M],tail[N];
int dep[N],las[N],now[N];
inline void add(int U,int V,int W)
{
++te;v[te]=V;w[te]=W;pre[te]=tail[U];tail[U]=te;
}
bool bfs()
{
memset(dep,0,sizeof(dep));
memcpy(now,tail,sizeof(now));
dep[st]=1;
vector<int>q;
int l=0;
q.push_back(st);
while(l<q.size())
{
int u=q[l++];
// cout<<"\n\nTEST: "<<u<<":";
for(int i=tail[u];i;i=pre[i])
if(w[i]&&!dep[v[i]])
{
// cout<<v[i]<<" ";
dep[v[i]]=dep[u]+1;
q.push_back(v[i]);
if(v[i]==ed) return 1;
}
}
return 0;
}
int dfs(int u,int val)
{
if(u==ed) return val;
int rest=val;
for(int &i=now[u];i&&rest;i=pre[i])
if(w[i]&&dep[v[i]]==dep[u]+1)
{
int d=dfs(v[i],min(v[i],min(rest,w[i])));
if(!d) dep[v[i]]=0;
else las[v[i]]=u,rest-=d,w[i]-=d,w[i^1]+=d;
}
return val-rest;
}
int main()
{
scanf("%d %d",&m,&n);
ed=n+1;
for(int i=1;i<=n;++i) //1~m:外 else 英国
if(i>m) add(st,i,1),add(i,st,0);
else add(i,ed,1),add(ed,i,0);
int x,y;
while(~scanf("%d %d",&x,&y))
{
if(x==-1&&y==-1) break;
add(x,y,0);add(y,x,INF);
}
while(bfs())
{
while(int d=dfs(st,INF)) Flow+=d;
}
printf("%d\n",Flow);
for(int i=tail[ed];i;i=pre[i])
if(w[i]) printf("%d %d\n",v[i],las[v[i]]);
}
P4016 负载平衡问题
题目描述
GG 公司有 nn 个沿铁路运输线环形排列的仓库,每个仓库存储的货物数量不等。如何用最少搬运量可以使 nn 个仓库的库存数量相同。搬运货物时,只能在相邻的仓库之间搬运。
输入格式
第一行一个正整数 nn,表示有 nn 个仓库。
第二行 nn 个正整数,表示 nn 个仓库的库存量。
输出格式
输出最少搬运量。
输入输出样例
输入 #1复制
5
17 9 14 16 4
输出 #1复制
11
说明/提示
1 \leq n \leq 1001≤n≤100。
这是一道数学题,不是网络流。
思路:
贪心+数学
先来讲下普通均分纸牌问题:
普通均分纸牌问题就是nn个小朋友排成一列,各自有a[i]a[i]张牌,每个人只能给相邻的人传递纸牌,问至少需要传递多少张纸牌才能使每个小朋友牌的个数相等。
\(T=sum/n\)分配完每个人有几张牌
\(gi=T-ai\)每个人需要分配几张牌(正为拿出负为拿入)
\(si=∑gj,j∈[1,i]\)。让前i个人平均还差多少牌。
让第一个人平均需要移动多少牌+让第二个人平均要移动多少牌+++++
环形均分纸牌模板
#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll n,a[105],s[105],sum,ans;
int main()
{
cin>>n;
for(int i=1;i<=n;++i) scanf("%d",&a[i]),sum+=a[i];
sum/=n;
for(int i=1;i<=n;++i)
a[i]-=sum,s[i]=s[i-1]+a[i];
sort(s+1,s+n+1);
sum=0;
for(int i=1;i<=n;++i) sum+=abs(s[n/2+1]-s[i]);
cout<<sum;
}
P3358 最长k可重区间集问题
给n个开区间,每个开区间长度为r-l,从中取出任意个区间,使对于任意一点,重叠在此点的区间不超过k个。
【思路】
不重叠的区间肯定能放在一起,于是连一连。
重点是怎么处理重叠的区间。
重叠的区间不连边,最多有k个哐哐哐重叠的区间,由起点向每个区间左边连边,左向右连边。
不想写了,复制粘贴吧!!!
首先一拿出来,这不就是匹配问题嘛?一个点最多匹配 kk 个区间。于是每个位置建一个点,然后连向覆盖自己的点,然后…好像不太对?其一他没给下标的取值范围,其二一个线段覆盖多个点,要么都覆盖要么都不覆盖,这个限制很难表示…
于是好像不知道从何处入手了。发现一个这样的性质,就是永远不会选择 kk 个以上交于 11 点的区间。也就是说,如果两个区间彼此之间没有交,就可以同时选;否则能不能同时选,看情况。这像极了「限制」,也就是如果两个区间之间没有交,那两者不存在限制;否则存在 kk 的限制。
根据一开始的匹配,可以猜到大致上用网络流是可行的。并且似乎网络流很适合用流量来表征限制。那么考虑,如果两个区间不存在限制,那么应该怎么办——网络流类似电流,所以此时如果串联的话,就代表着可以同时选;那么如果存在限制,就意味着不能串联。根据这一点,考虑如何串联。发现本质上是将两个不交的区间中间连 f=\infty,c=0f=∞,c=0 的边。
这一点就引申出两个建图方法,其本质是相同的:
1、建立一个超级源 \rm SS 和一个源 \rm S'S
′
,中间连 f=k,c=0f=k,c=0 的边,目的是提供初始流量。\rm S'S
′
向每个区间的左端点连一条 f=1,c=-1f=1,c=−1 边。然后区间左端点向右端点连边 f=1,c=-lenf=1,c=−len 表示贡献,每个右端点再向 \rm T T 连边即可。如果两个区间不交,就由一个区间的 rr 连向另一个区间的 ll (当然要按秩啦)。思考这样做的合理性,对于相交的区间,一定是并联;否则的话就是串联(其实叫做混连,但是问题不大)。
2、建立一个源 \rm SS 连向数轴上的 00 位置,f=k,c=0f=k,c=0。然后数轴上每个 i>0i>0 向 i+1i+1 连边 f=k,c=0f=k,c=0。最后 maxrightmaxright 向 \rm TT 连边。对于一个区间,连法跟1相同。
注意:
1、为什么要拆点?此处拆点的作用值得注意。对于一个区间,本质上应该抽象成一个点。但是在流图里是不存在「点权」这个概念的。所以需要把点权转边权,拆点的作用便在于此。
2、其实上面两个方法,可以通过初中物理里面什么「判断两个电路图是否等价」的知识来解决的233
3、由于本题保证了「开区间」,所以可以直接 l\to r,len=r-ll→r,len=r−l 。当然如果是闭区间,只需要改成 l\to r+1l→r+1 即可。
4、上面的第二个方案,发现最终可能存在很多数轴上的点 ii 只与 i-1,i+1i−1,i+1 连了 f=k,c=0f=k,c=0 的边,所以是没用的,离散化掉就好了。
P4015 运输问题
有n个商店m个仓库,每个商店需要x的货物,第i个仓库运一个单位的货物到第j个商店的运费为\(c[i][j]\),求最小最大费用。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=5e3+5,M=1e5+5,INF=1e9;
int n,m,st,ed,Flow,Cost;
int tail[N];
int te=1,v[M],f[M],pre[M];
ll dis[N],w[M];
bool vis[N];
inline void add(int U,int V,int W,int F)
{
++te;
v[te]=V;w[te]=W;f[te]=F;pre[te]=tail[U];
tail[U]=te;
}
bool spfa()
{
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
deque<int>q;
dis[ed]=0;
q.push_back(ed);
while(q.size())
{
int u=q.front();
q.pop_front();
vis[u]=0;
for(int i=tail[u];i;i=pre[i])
if(f[i^1]&&dis[v[i]]>dis[u]-w[i])
{
dis[v[i]]=dis[u]-w[i];
if(!vis[v[i]])
{
vis[v[i]]=1;
if(q.empty()||dis[q.front()]<dis[v[i]])q.push_back(v[i]);
else q.push_front(v[i]);
}
}
}
return dis[st]<dis[N-1];
}
inline int dfs(int u,int val)
{
vis[u]=1;
if(u==ed)return val;
int rest=val;
for(int i=tail[u];i&&rest;i=pre[i])
if(!vis[v[i]]&&f[i]&&dis[v[i]]+w[i]==dis[u])
{
int d=dfs(v[i],min(f[i],rest));
if(!d) dis[v[i]]=0;
else rest-=d,f[i]-=d,f[i^1]+=d;
}
return val-rest;
}
void work()
{
while(spfa())
{
vis[ed]=1;
while(vis[ed])
{
memset(vis,0,sizeof(vis));
int d=dfs(st,INF);
Flow+=d;
Cost+=1ll*d*dis[st];
}
}
}
int a[105],b[105];
ll c[105][105];
int main()
{
scanf("%d %d",&m,&n);
for(int i=1;i<=m;++i) scanf("%d",&a[i]);//仓库
for(int i=1;i<=n;++i) scanf("%d",&b[i]);//商店
for(int i=1;i<=m;++i)
for(int j=1;j<=n;++j)
scanf("%d",&c[i][j]);
st=0;ed=n+m+1;te=1;
for(int i=1;i<=m;++i) add(st,i,0,a[i]),add(i,st,0,0);
for(int i=1;i<=n;++i) add(m+i,ed,0,b[i]),add(ed,m+i,0,0);
for(int i=1;i<=m;++i)
for(int j=1;j<=n;++j)
add(i,m+j,c[i][j],INF),add(m+j,i,-c[i][j],0);
work();
printf("%d\n",Cost);
st=0;ed=n+m+1;te=1;Flow=Cost=0;
for(int i=st;i<=ed;++i) tail[i]=0;
for(int i=1;i<=m;++i) add(st,i,0,a[i]),add(i,st,0,0);
for(int i=1;i<=n;++i) add(m+i,ed,0,b[i]),add(ed,m+i,0,0);
for(int i=1;i<=m;++i)
for(int j=1;j<=n;++j)
add(i,m+j,-c[i][j],INF),add(m+j,i,c[i][j],0);
work();
printf("%d\n",-Cost);
}
P2762 太空飞行计划问题

最大权闭合子图模板题。
P2770 航空路线问题

找两条除ST外不重叠的ST路。
然后顺着输出,倒着输出。
P3254 圆桌问题

\(st\)连单位容量为\(ri,\)桌子连\(ed\)容量为\(ci,\)单位向桌子连容量为1的边。
P4012 深海机器人问题

每个点向上向右的点连边。每个点拆分成两个点,连一条权值为-w容量为1的边,连一条权值为0容量为INF的边。每个起点向st连边,每个终点向ed连边,容量1权值0。跑一遍费用流。
P2763 试题库问题

一种类型可能需要x种题,一道题可能多种类型都需要,但一道题只能满足一种类型。
st向每道题连容量为1的边,类型向ed连容量为x的边,每道题向所属的所有类型连传递边,求最大流。从st出发,对于st出发容量为0的每道题,求本题的哪个目标非st的出边的反向边容量为1。(是不是st其实不重要,因为如果目标为st,即本边为st到i的反向边,而st到i的边容量为0)
P2766 最长不下降子序列问题

DP求问题1,网络流求问题2和3,每个点拆成两个点流量为1,第三问的时候1和n流量为INF,每个点向小于等于他并且长度+1等于此点长度的点,容量为1。求最大流。第三题就直接在第二问的残留网络上加(1,1+n,INF)和(n,n+n,INF)的边。
特判一下n为1和n为2的时候。(因为本题好像没有n为2的数据点所以没写,但正式考试还是要考虑的。
如果ans是1的话,x1和x2无限用就会跑无限次就会超时,所以ans为1的时候也要特判。
#include<bits/stdc++.h>
using namespace std;
const int N=1105,M=1e5+5,INF=1e7+5;
int n,st,ed,ans,Flow;
int a[N],f[N],dep[N],now[N];
int te=1,v[M],w[M],pre[M],tail[N];
inline void add(int x,int y,int z)
{
++te;v[te]=y;w[te]=z;pre[te]=tail[x];tail[x]=te;
}
bool bfs()
{
memset(dep,0,sizeof(dep));
memcpy(now,tail,sizeof(now));
dep[st]=1;
vector<int>q;
int l=0;
q.push_back(st);
while(l<q.size())
{
int u=q[l++];
for(int i=tail[u];i;i=pre[i])
if(w[i]&&!dep[v[i]])
{
dep[v[i]]=dep[u]+1;
q.push_back(v[i]);
if(v[i]==ed) return 1;
}
}
return 0;
}
int dfs(int u,int val)
{
if(u==ed) return val;
int rest=val;
for(int &i=now[u];i&&rest;i=pre[i])
if(w[i]&&dep[v[i]]==dep[u]+1)
{
int d=dfs(v[i],min(v[i],min(rest,w[i])));
if(!d) dep[v[i]]=0;
else rest-=d,w[i]-=d,w[i^1]+=d;
}
return val-rest;
}
int main()
{
scanf("%d",&n);
st=0;ed=n*2+1;
for(int i=1;i<=n;++i)scanf("%d",&a[i]),f[i]=1;
if(n==1)
{
printf("1\n1\n1\n");
return 0;
}
for(int i=1;i<=n;++i)
for(int j=1;j<i;++j)
if(a[i]>=a[j]) f[i]=max(f[i],f[j]+1);
for(int i=1;i<=n;++i) ans=max(ans,f[i]);
printf("%d\n",ans);
for(int i=1;i<=n;++i) if(f[i]==1) add(st,i,1),add(i,st,0);
for(int i=1;i<=n;++i) if(f[i]==ans) add(n+i,ed,1),add(ed,n+i,0);
for(int i=1;i<=n;++i) add(i,n+i,1),add(n+i,i,0);
for(int i=1;i<=n;++i)
for(int j=1;j<i;++j)
if(a[j]<=a[i]&&f[j]+1==f[i]) add(n+j,i,1),add(i,n+j,0);
while(bfs())
{
while(int d=dfs(st,INF)) Flow+=d;
}
printf("%d\n",Flow);
if(ans!=1)
{
add(st,1,INF),add(1,st,0);
add(1,n+1,INF),add(n+1,1,0);
if(f[n]==ans) add(n+n,ed,INF),add(ed,n+n,0),add(n,n+n,INF),add(n+n,n,0);
while(bfs())
{
while(int d=dfs(st,INF)) Flow+=d;
}
}
printf("%d\n",Flow);
}
P4013 数字梯形问题

以下所有的点点间都指点和它左下或者右下的点。
顶部和st连容量为1的边,底部和ed连传递边。(只有m条路径,每个起点只能用一次QAQ)
对于问题1:
拆点,点和点’间容量为1,费用为-val,点点间连传递边,跑最小费用最大路,输出-Cost。
对于问题2:
不拆点,点点间连容量为1,权值为-val(val是指v的val值)的边。
对于问题3:
在问题二的基础上容量改为INF。
P1251 餐巾计划问题

这是一道最小费用(费用指单价)最大流的题目。
首先,我们拆点,将一天拆成晚上和早上,每天晚上会受到脏餐巾(来源:当天早上用完的餐巾,在这道题中可理解为从原点获得),每天早上又有干净的餐巾(来源:购买、快洗店、慢洗店)。
1.从原点向每一天晚上连一条流量为当天所用餐巾x,费用为0的边,表示每天晚上从起点获得x条脏餐巾。
2.从每一天早上向汇点连一条流量为当天所用餐巾x,费用为0的边,每天白天,表示向汇点提供x条干净的餐巾,流满时表示第i天的餐巾够用 。 3.从每一天晚上向第二天晚上连一条流量为INF,费用为0的边,表示每天晚上可以将脏餐巾留到第二天晚上(注意不是早上,因为脏餐巾在早上不可以使用)。
4.从每一天晚上向这一天+快洗所用天数t1的那一天早上连一条流量为INF,费用为快洗所用钱数的边,表示每天晚上可以送去快洗部,在地i+t1天早上收到餐巾 。
5.同理,从每一天晚上向这一天+慢洗所用天数t2的那一天早上连一条流量为INF,费用为慢洗所用钱数的边,表示每天晚上可以送去慢洗部,在地i+t2天早上收到餐巾 。
6.从起点向每一天早上连一条流量为INF,费用为购买餐巾所用钱数的边,表示每天早上可以购买餐巾 。 注意,以上6点需要建反向边!3~6点需要做判断(即连向的边必须<=n)
P3355 骑士共存问题

在原图上的X点,找到能攻击这个点的点,然后推出新的X点,然后会发现图长这样:
于是就成了二分图方格取数模板题。
P3356 火星探险问题

题面有点长,但废话很多,说白了就是:从(1,1)到(p,q)最多可以走n条路,只能向下向右走,有的点可以走有的点不能走,可以走的点有一个权值1,只能被取一次,求取出的权值和最大是多少。
对于这道题只有一个想法:
朋友,听说过,方格取数吗?
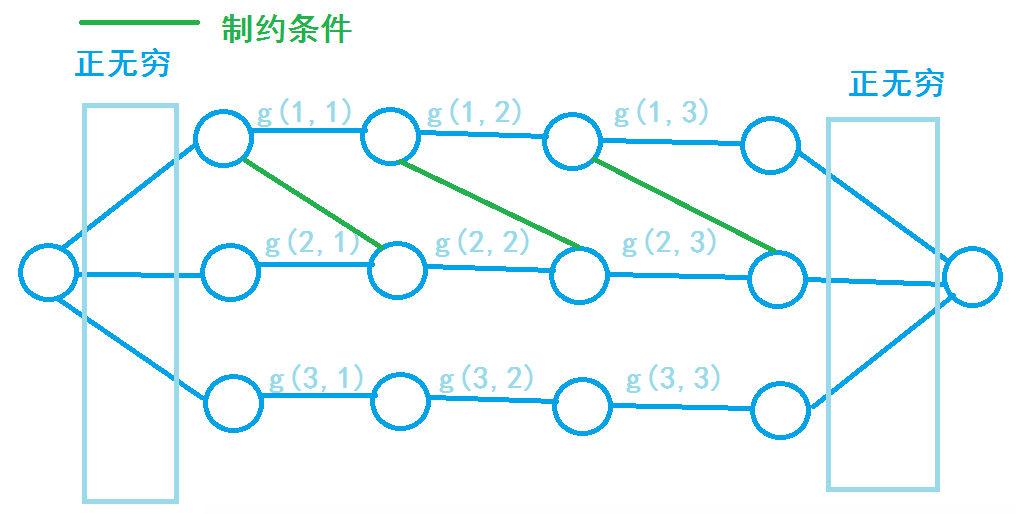
P2764 最小路径覆盖问题

精简题意(原题写的太不是东西了):在有向图里找k条不相交的路径,使其经过所有的点。
首先,很重要的一点:如果两条路,一条路的终点和另一条路的起点相连,两条路就可以合并成一条路。
于是把每个点分为路的起点和终点两种状态,起点连st,终点连ed,如果有边就v的起点连u的终点,得到的最大流就是被合并掉的路的数量。
一开始假定每个点都是一条路,所以点数-Flow就是剩下的路。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号