摘要：# T1 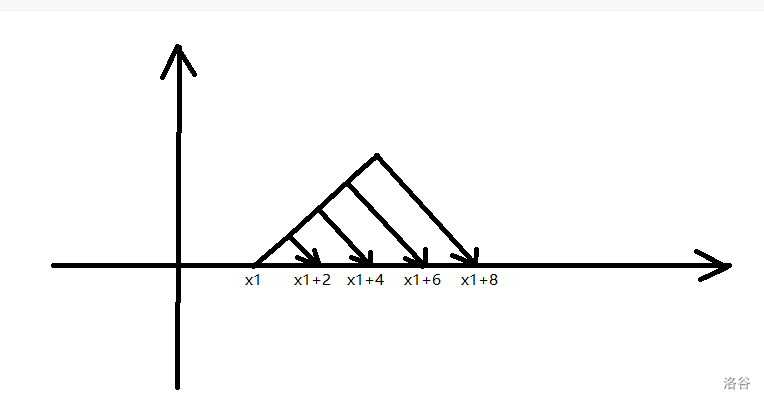 如图，从 $x_1$ 能且只能走到 $x_1+2,x_1+4,x_1+6...$ 设 $f[x]$ 表示从 $x_1$ 走到 $x$ 的方案数，那么如果 $x-x 阅读全文

摘要：# T1 假设交换了 $a[i]$ 和 $a[i+1]$ ，那么 $a[1...i-1]$ ， $a[i+2...n]$ 与这两个数构成的逆序对不变。只有 $a[i]$ 和 $a[i+1]$ 两个数构成的逆序对可能发生改变。 如果 $a[i]a[i+1]$ ，那么逆序对个数$-1$。 **另外，此题 阅读全文

摘要：## [P2756 飞行员配对方案问题](https://www.luogu.com.cn/problem/P2756) 这是一个裸的二分图最大匹配问题，可以用匈牙利算法解决，当然也可以网络流的最大流解决。 我们将源点和每一个英国飞行员连一条边权为1的边，将每一个外籍飞行员和汇点连边权为1的边，再将 阅读全文

摘要：# T1 首先题目没有强制让我们一起算 $k^{r(p)}+r^2(p)$ ，我们可以把它拆成两部分，一部分是 $k^{r(p)}$ ，一部分是 $r^2(p)$ 。 考虑递推求解两个部分。先看第一个部分。设 $n$ 的全排列的逆序对个数分别是 $p_1,p_2,...,p_{n!}$ ，并假设我们 阅读全文