2023.6.18拷逝
T1
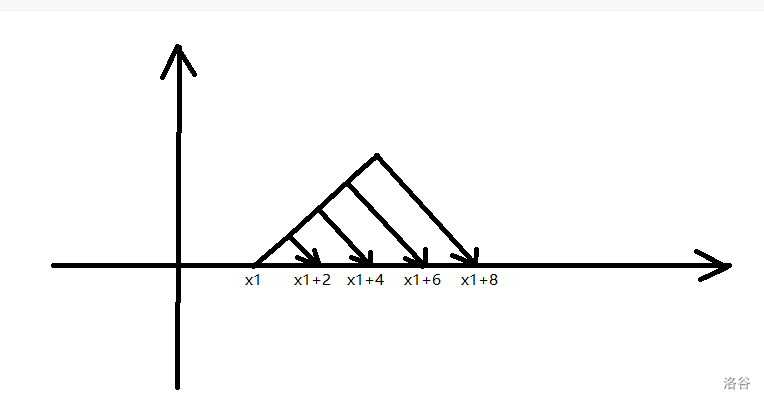
如图,从 \(x_1\) 能且只能走到 \(x_1+2,x_1+4,x_1+6...\)
设 \(f[x]\) 表示从 \(x_1\) 走到 \(x\) 的方案数,那么如果 \(x-x_1\) 是偶数,那么 \(f[x]=f[x-2]+f[x-4]+...+f[x_1]\) ,否则 \(f[x]=0\) 。初始值: \(f[x_1]=1\) 。
考虑 \(f[x]\) 的前几项。 \(f[x_1]=1,f[x_1+2]=1,f[x_1+4]=2,f[x_1+6]=4,f[x_1+8]=8...\) 。于是我们很高兴地发现 \(f[x]=2^{(x-x_1)/2-1}\),然后打一个快速幂就行。
\(code:\)
#include<iostream>
#include<cstdio>
using namespace std;
const long long mod=100000007;
long long t,n,m,ans;
long long f(long long x,long long y){
long long s=x;x=1;
while(y){
if(y&1)
x=x*s%mod;
s=s*s%mod;y>>=1;
}
return x;
}
int main(){
freopen("gta.in","r",stdin);
freopen("gta.out","w",stdout);
scanf("%lld",&t);
while(t--){
scanf("%lld%lld",&n,&m);
if((m-n)&1)
printf("0\n");
else if(m==n)
printf("1\n");
else{
printf("%lld\n",f(2,(m-n)/2-1));
}
}
fclose(stdin);fclose(stdout);
return 0;
}
T2
首先介绍一种错误的方法。
设\(f[i]\)表示状态为\(i\)时的最大收益,其中\(i\)的具体含义是:把\(i\)拆成二进制,从低位起第\(j\)个数为\(1\)表示选择第\(j\)个士兵,否则不选第\(j\)个士兵。
状态转移方程:\(f[i]=max(f[i],f[p]\&(a[j]\) \(xor\) \(a[k]))\),其中\(p=i-(2^{j-1}-2^{k-1})\)
但是这个方程有问题。假设当前的 \(a[j]\) \(xor\) \(a[k]=(0011)_2\) 。当\(f[p]\)最优时,\(f[p]\)可能储存的答案是 \((1100)_2\) ,此时经过计算,\(f[i]=0\)。但是,如果在 \(p\) 状态下用另一种运算方式得到\((0011)_2\),那么\(f[i]=(1100)_2\)。也就是说,这个 \(DP\) 不满足最优子结构。
肿么办呢?我们可以仍然遍历上面的每一个状态,但是将\(DP\)改成搜索。如果当前状态的二进制中\(1\)的个数等于\(n\times 2\),那么相当于产生了一种合理的选兵方案。此时就可以直接进行深搜,找到最优的排列顺序,然后找出敌方的最优排列顺序,更新答案。
\(code:\)
#include<iostream>
#include<cstdio>
using namespace std;
const long long MAXN=2147483647;
long long n,a[10005],b[10005],c[10005],ans,ans1,ans2,vis[10005];
void dfs1(int x,int sum,long long val){
if(sum==n*2){
ans1=max(ans1,val);
return void();
}
if(val<=ans)
return ;
if(vis[x]){
dfs1(x+1,sum,val);return ;
}
for(int i=1;i<=n*2;++i)
if(!vis[i]&&i!=x){
vis[i]=1;vis[x]=1;
dfs1(x+1,sum+2,val&(b[i]^b[x]));
vis[i]=0;vis[x]=0;
}
return ;
}
void dfs2(int x,int sum,long long val){
if(sum==n*2){
ans2=max(ans2,val);
return ;
}
if(vis[x]){
dfs2(x+1,sum,val);return ;
}
for(int i=1;i<=n*2;++i)
if(!vis[i]&&i!=x){
vis[i]=1;vis[x]=1;
dfs2(x+1,sum+2,val&(c[i]^c[x]));
vis[i]=0;vis[x]=0;
}
return ;
}
int main(){
//freopen("vip.in","r",stdin);
//freopen("vip.out","w",stdout);
scanf("%lld",&n);
for(int i=1;i<=n*4;++i)
scanf("%lld",&a[i]);
ans=-1e18;
for(int i=0;i<(1<<(n*4));++i){
int tmp=i,cnt=0,x=0,y=0;ans1=0,ans2=0;
while(tmp){
if(tmp&1)
++cnt;
tmp>>=1;
}
if(cnt!=n*2)
continue;
for(int j=1;j<=n*4;++j){
if((i>>(j-1))&1) b[++x]=a[j];
else c[++y]=a[j];
}
dfs1(1,0,MAXN);
if(ans1<=ans)
continue;
dfs2(1,0,MAXN);
ans=max(ans,ans1-ans2);
}
printf("%lld\n",ans);
fclose(stdin);fclose(stdout);
return 0;
}
T3(84pts)
正解需要用到 \(tarjan\) ,目前还没有写出。但是数据太水了,导致有一种错误的做法能拿到84分。
统计每一个点的度,如果一个点的度为\(1\),就\(++ans\),最后输出\(ans/2.0\)上取整即可。
\(code:\)
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=1e6+5;
int tot,n,m,x,y,ans,cnt,head[maxn],ver[maxn],nxt[maxn],in[maxn];
bool vis[maxn],r[maxn];
int read(){
char p;int s=0,w=1;
while(1){
p=getchar();
if(p=='-'||(p>='0'&&p<='9'))
break;
}
while(1){
if(p=='-')
w*=-1;
else if(p>='0'&&p<='9')
s=s*10+p-'0';
else break;
p=getchar();
}
return s*w;
}
int main(){
freopen("ring.in","r",stdin);
freopen("ring.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i){
x=read();y=read();
++in[x];++in[y];
}
for(int i=1;i<=n;++i)
if(in[i]==1)
++ans;
if(ans&1)
ans=ans/2+1;
else
ans=ans/2;
printf("%d\n",ans);
fclose(stdin);fclose(stdout);
return 0;
}
T4
树形背包好题。
设 \(f[x][i][0/1][0/1]\) 表示以 \(x\) 为根的子树中共放了 \(i\) 个监听装置,其中 \(x\) 点放没放装置, \(x\) 点有没有被监听到的方案数(在以 \(x\) 为根的子树中除 \(x\) 外的其它结点都被监听到了)
状态转移方程:
①:\(x\)没有被监听,也没有放装置。此时子节点一定不能放装置。\(f[x][i+j][0][0]= \sum f[x][i][0][0]\times f[v][j][0][1]\)
②:\(x\)没有被监听,但放了装置。此时子节点同样一定不能放装置,但它有没有被以它为根的子树内的节点监听有无所谓了。
\(f[x][i+j][1][0]= \sum f[x][i][1][0]\times (f[v][j][0][0]+f[v][j][0][1])\)
③:\(x\)没放装置,但被监听了。
如果\(x\)在这之前已经被监听,那么\(v\)放不放装置无所谓;而如果\(x\)在这之前没有被监听,那么\(v\)处必须放装置。因为\(x\)没放装置,所以\(v\)必须被以它为根的子树内的节点监听。
\(f[x][i+j][0][1]= \sum f[x][i][0][1]\times (f[v][j][0][1]+f[v][j][1][1])+f[x][i][0][0]\times f[v][j][1][1]\)
④:\(x\)放了装置,也被监听了。
如果\(x\)在这之前已经被监听,那么\(v\)随意;而如果\(x\)在这之前没有被监听,那么\(v\)处必须放装置。因为\(x\)放了装置,所以\(v\)是否被以它为根的子树内的节点监听无所谓。
\(f[x][i+j][1][1]= \sum f[x][i][1][0]\times (f[v][j][1][0]+f[v][j][1][1])+f[x][i][1][1]\times (f[v][j][1][1]+f[v][j][1][0]+f[v][j][0][1]+f[v][j][0][0])\)
\(code:\)
#include<iostream>
#include<cstdio>
using namespace std;
const int mod=1e9+7,l=1e5+5;
int n,k,a,b,tot,head[l<<1],ver[l<<1],nxt[l<<1];
int dp[l][105][2][2],tmp[l][2][2],siz[l];
void add(int x,int y){
nxt[++tot]=head[x];head[x]=tot;ver[tot]=y;
}
void dfs(int x,int fa){
siz[x]=dp[x][0][0][0]=dp[x][1][1][0]=1;
for(int t=head[x];t;t=nxt[t]){
int v=ver[t];
if(v!=fa){
dfs(v,x);
for(int i=0;i<=min(k,siz[x]);++i){
tmp[i][0][0]=dp[x][i][0][0];dp[x][i][0][0]=0;
tmp[i][0][1]=dp[x][i][0][1];dp[x][i][0][1]=0;
tmp[i][1][0]=dp[x][i][1][0];dp[x][i][1][0]=0;
tmp[i][1][1]=dp[x][i][1][1];dp[x][i][1][1]=0;
}
for(int i=0;i<=min(k,siz[x]);++i)
for(int j=0;j<=min(k-i,siz[v]);++j){
dp[x][i+j][0][0]=(dp[x][i+j][0][0]+1ll*tmp[i][0][0]*dp[v][j][0][1]%mod)%mod;
dp[x][i+j][0][1]=(dp[x][i+j][0][1]+1ll*tmp[i][0][1]*(dp[v][j][0][1]+dp[v][j][1][1])%mod)%mod;
dp[x][i+j][0][1]=(dp[x][i+j][0][1]+1ll*tmp[i][0][0]*dp[v][j][1][1]%mod)%mod;
dp[x][i+j][1][0]=(dp[x][i+j][1][0]+1ll*tmp[i][1][0]*(dp[v][j][0][0]+dp[v][j][0][1])%mod)%mod;
dp[x][i+j][1][1]=(dp[x][i+j][1][1]+1ll*tmp[i][1][0]*(dp[v][j][1][1]+dp[v][j][1][0])%mod)%mod;
dp[x][i+j][1][1]=(dp[x][i+j][1][1]+1ll*tmp[i][1][1]*(1ll*(dp[v][j][0][0]+dp[v][j][0][1])+1ll*(dp[v][j][1][0]+dp[v][j][1][1]))%mod)%mod;
}
siz[x]+=siz[v];
}
}
return ;
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<n;++i)
scanf("%d%d",&a,&b),add(a,b),add(b,a);
dfs(1,0);
printf("%d\n",(dp[1][k][1][1]+dp[1][k][0][1])%mod);
fclose(stdin);fclose(stdout);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号