网络流24题(5/24)

P2756 飞行员配对方案问题

这是一个裸的二分图最大匹配问题，可以用匈牙利算法解决，当然也可以网络流的最大流解决。

我们将源点和每一个英国飞行员连一条边权为1的边，将每一个外籍飞行员和汇点连边权为1的边，再将每一对匹配的英军飞行员和外籍飞行员之间连一条边权为1的边。跑这个图的最大流，就得到了二分图的最大匹配。

\(code:\)

int main(){
	scanf("%d%d",&m,&n);
	while(1){
		scanf("%d%d",&u,&v); 
		if(u==-1&&v==-1)
			break;
		add(u,v);
	}
	for(int i=1;i<=m;++i){
		for(int j=1;j<=n;++j)
			vis[j]=0;
		if(dfs(i))
			++ans;
	}
	printf("%d\n",ans);
	for(int i=1;i<=n;++i)
		if(match[i])
			printf("%d %d\n",match[i],i);
	return 0;
} 

P2765魔术球问题

考虑每一个新放的球，它要么是单独放一个柱子上，要么是放到其他球上面。

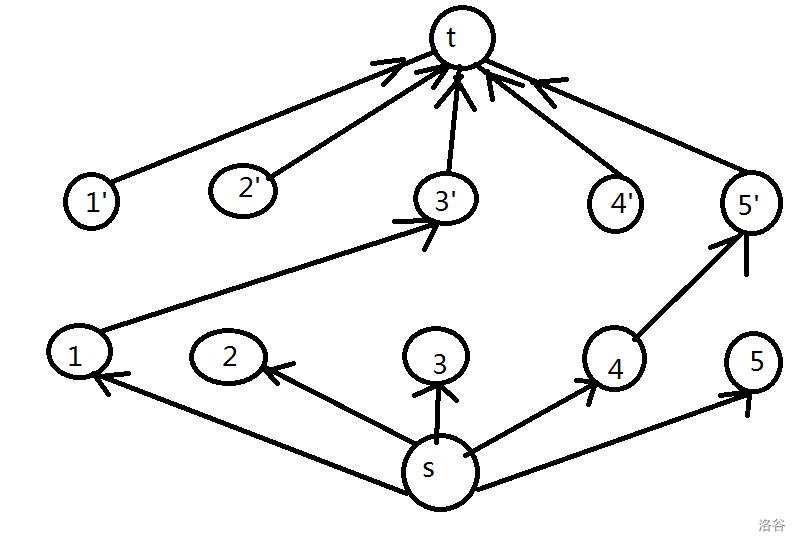
我们将每一个球 \(i\) 拆成 \(i\) 和 \(i'\) 。将源点 \(s\) 和 \(i\) 连一条流量为1的边，再将 \(i'\) 和汇点 \(t\) 连一条流量为1的边，表示每一个球能且只能使用一次。

再考虑当前的球能放到哪些球上面。设这些球为 \(j\) ,那么再将 \(j\) 向 \(i'\) 连一条边权为1的边，表示 \(j\) 球后面能接 \(i\) 球。

这样，每放进一个球，就跑一遍 \(dinic\)，如果能够找到增广路，说明当前的球能放到其他球上面，否则说明当前的球只能自立门户。

\(code:\)

int dfs(int x,int sum){
	if(x==t)
		return sum;
	int re=sum,k;
	for(int i=now[x];i&&re;i=nxt[i])
		if(d[ver[i]]==d[x]+1&&e[i]){
			now[x]=i;
			k=dfs(ver[i],min(re,e[i]));
			if(!k)
				d[ver[i]]=0;
			else
				nx[(x+1)>>1]=((ver[i]+1)>>1);
			re-=k;e[i]-=k;e[i^1]+=k;
		}
	return sum-re;
}
int main(){
	scanf("%d",&n);
	s=0;t=10001;tot=1;
	for(int i=1;i<=5000;++i){
		//add(i*2-1,i*2,1);add(i*2,i*2-1,0);
		add(s,i*2-1,1);add(i*2-1,s,0);
		add(i*2,t,1);add(t,i*2,0);
		for(int j=1;j*j<i*2;++j)
			if(j*j-i>0)
				add((j*j-i)*2-1,i*2,1),add(i*2,(j*j-i)*2-1,0);
		int sum=0,f=0;
		while(bfs())
			while(sum=dfs(0,1e9))
				f+=sum;
		if(!f){
			++cnt;box[cnt]=i;
		}
		if(cnt>n){
			ans=i-1;break;
		} 
	}
	printf("%d\n",ans); 
	for(int i=1;i<=n;++i){
		int x=box[i];
		while(x!=(10001+1)/2&&x!=0){
			printf("%d ",x);
			x=nx[x];
		}
		printf("\n");
	}
	return 0;
}

P2754 [CTSC1999]家园 / 星际转移问题

看到时间，想到将每个节点拆成500个分点，代表时刻 \(1\)~\(500\) 。

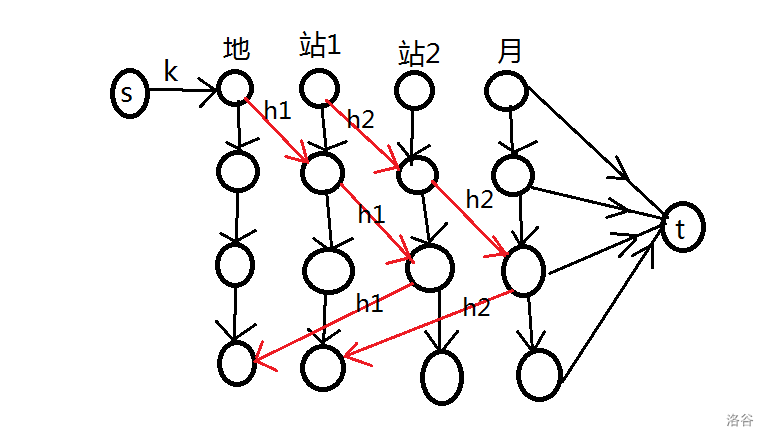
假设某个飞船 \(t\) 时刻在节点 \(p[t]\) ，那么我们把节点 \(p[t]\) 的第 \(t\) 个分点连向节点 \(p[t+1]\) 的第 \(t+1\) 个分点，权值为该飞船容纳的人数 \(h\) 。以上过程模拟了飞船的周期性穿梭。

接下来，对于每一个节点的任何一个分点，向它的下一个分点连权值为 \(inf\) 的边，模拟人停留在某个星球。

最后是 \(s\) 向地球的第一个分点连权值为 \(k\) 的边，月球的每一个分点向汇点连一条权值为 \(inf\) 的边。

怎么判断是否无解以及最短时间呢？考虑二分答案。如果当前的时间为 \(t\) ，那么只能在每个点的第 \(1\)~\(t\) 个分点上跑最大流。如果当前最大流是 \(k\) ，说明所有人都能在 \(t\) 时间内转移到月球，符合题意；否则不符合题意。这样，就能二分出最短时间。而如果最大流永远达不到 \(k\) ，那么无解。

\(code:\)

int main(){
	scanf("%d%d%d",&n,&m,&k);
	tot=1;s=0;t=(n+2)*501+1;
	for(int i=1;i<=m;++i){
		scanf("%d%d",&h,&u);
		for(int j=1;j<=u;++j){
			scanf("%d",&p[j]);
			if(p[j]==-1)
				p[j]=n+2;
			else
				++p[j];
		}
		for(int j=1;j<=500;++j)
			add(p[(j-1)%u+1]+(j-1)*(n+2),p[j%u+1]+j*(n+2),h),add(p[j%u+1]+j*(n+2),p[(j-1)%u+1]+(j-1)*(n+2),0);
		//cout<<p[(j-1)%r+1]+(j-1)*(n+2)<<" "<<p[j%r+1]+j*(n+2)<<endl;
	}
	for(int i=1;i<=n+2;++i)
		for(int j=1;j<=500;++j)
			add(i+(n+2)*(j-1),i+(n+2)*j,1e9),add(i+(n+2)*j,i+(n+2)*(j-1),0);
	add(0,1,k);add(1,0,0);
	for(int i=1;i<=501;++i)
		add((n+2)*i,t,1e9),add(t,(n+2)*i,0);
	l=1,r=501;
	while(l<r){
		for(int i=1;i<=tot;++i)
			edge[i]=e[i];
		for(int i=0;i<=t;++i)
			now[i]=0;
		mid=(l+r)>>1;
		int sum=0,f=0;
		while(bfs())
			while(sum=dfs(0,1e9))
				f+=sum;
		if(f<k)
			l=mid+1;
		else
			r=mid;
	}
	if(r==501)
		printf("0\n");
	else
		printf("%d\n",r-1);
	return 0;
}

P2762太空飞行计划问题

这道题是一个经典的“最大权闭合图”问题。

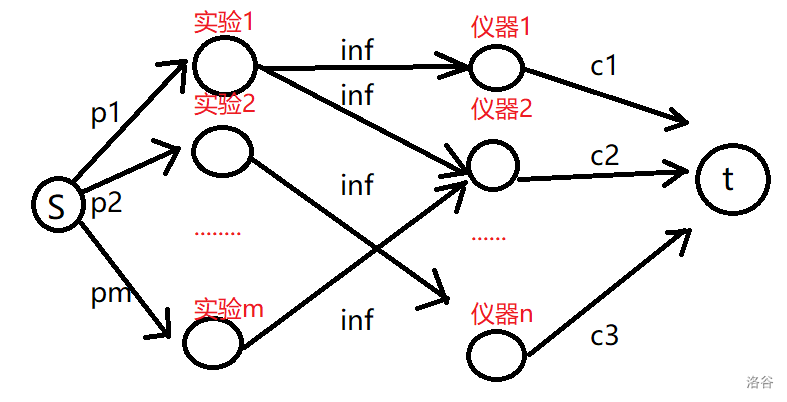
对于每个实验，由源点向他连一条流量为 \(p_i\) 的边。( \(p_i\) 指该实验的收益)

对于每个实验所需要的所有器材，由实验向器材连一条流量为 \(inf\) 的边。

对于每个器材，由它向汇点连一条流量为 \(c_i\) 的边。( \(c_i\) 指该器材的代价)

其中割掉一个源点指向实验的边表示不要这个实验，割掉一条器材指向汇点的边表示需要支付该器材的费用。然后就可以跑最小割。答案就是所有实验的收益减去最小割的值。

\(code:\)

int main(){
	scanf("%d%d",&m,&n);
	tot=1;s=0;t=n+m+1;
	for(int i=1;i<=m;++i){
		scanf("%d",&w);
		all+=w;
		add(s,i,w);add(i,s,0);
		input(i);//input是题目中用到的输入函数
	}
	for(int i=1;i<=n;++i){
		scanf("%d",&w2);
		add(i+m,t,w2);add(t,i+m,0);
	}
	int sum=0;
	while(bfs())
		while(sum=dinic(s,1e9))
			ans+=sum;
	for(int i=1;i<=m;++i)
		if(d[i]>0)
			printf("%d ",i);
	printf("\n");
	for(int i=m+1;i<=n+m;++i)
		if(d[i]>0)
			printf("%d ",i-m);
	printf("\n%d\n",all-ans);
	return 0;
}

P1251餐巾计划问题

费用流好题。

首先将每个点 \(i\) 拆成两个点 \(i\) ，\(i'\) ，代表早上和晚上。

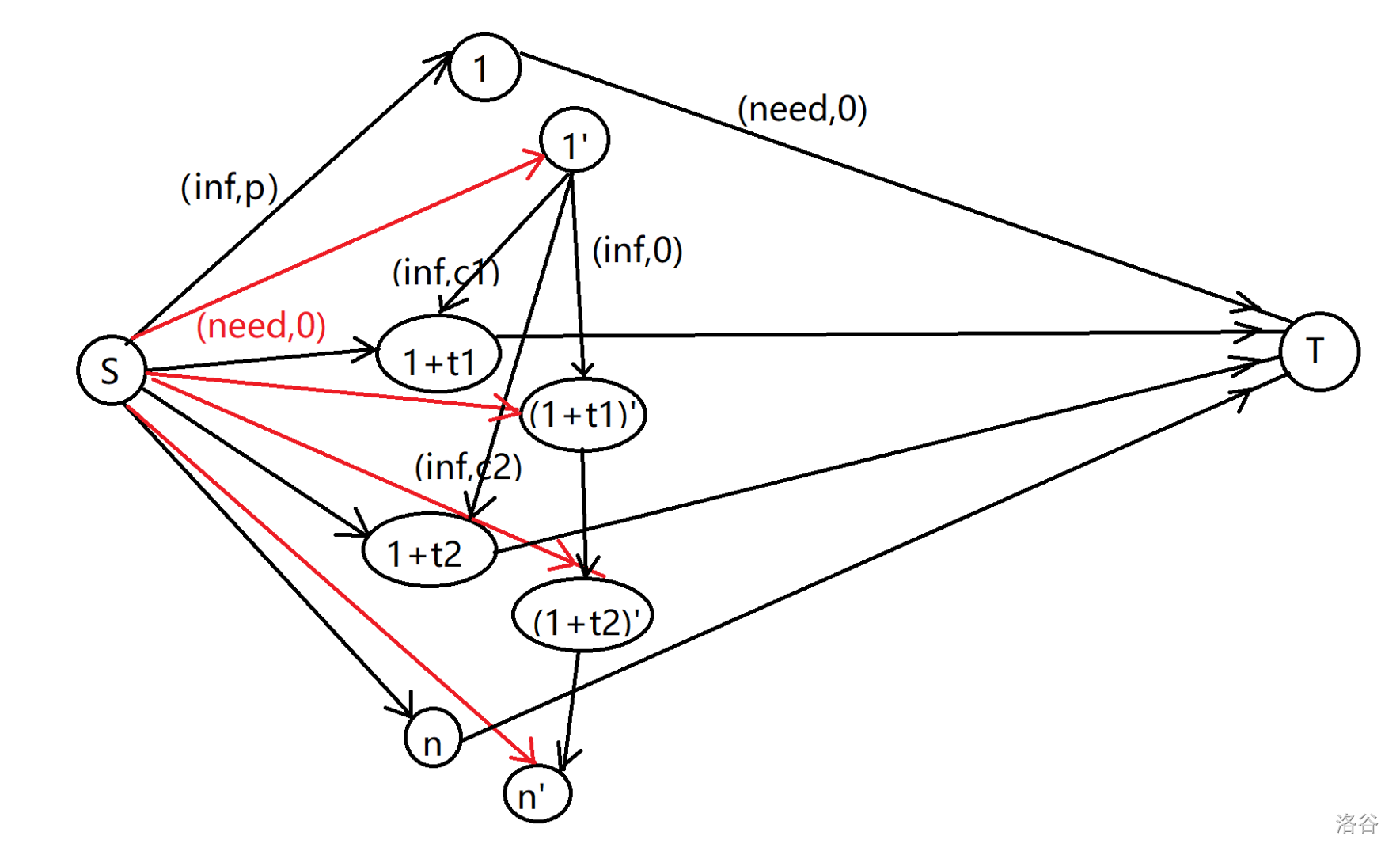
对于每个早上的点，由源点向他连一条流量为 \(INF\) ,费用为 \(p\) 的边，表示早上可以购买无限条费用为 \(p\) 的毛巾。

对于每个早上的点，由它向汇点连一条流量为 \(need[i]\) ，费用为 \(0\) 的边，表示每天要交出这些毛巾。

对于每个晚上的点，由源点向它连一条流量为 \(need[i]\) ，费用为 \(0\) 的边，表示每天会产生 \(need[i]\) 条脏毛巾。

对于每个晚上的点，向下一个晚上的点连一条流量为 \(INF\) ，费用为 \(0\) 的边，表示每天晚上可以把任意多条毛巾留给第二天。

对于每个晚上的点 \(i'\) ，由它分别向 \(i+t_1\) ， \(i+t_2\) 连一条流量为 \(INF\) ，费用为 \(c_1\)，\(c_2\) 的边，表示每天晚上可以将任意多条毛巾送到快洗部，慢洗部洗。

个人认为，本题的巧妙之处是，由早上的点向汇点连 \(need[i]\) 的边，并由源点向晚上连一条 \(need[i]\) 的边。这样很好地表示了每天会吃掉 \(need[i]\) 条干净毛巾，又会吐出 \(need[i]\) 条脏毛巾供以后再用。

\(code:\)

scanf("%lld",&n);
tot=1;s=0;t=n*2+1;
for(int i=1;i<=n;++i)
    scanf("%lld",&day[i]);
scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&e);
for(int i=1;i<=n;++i){
    add(s,i,1e9,a);add(i,s,0,-a);
    add(i,t,day[i],0);add(t,i,0,0);
    add(s,i+n,day[i],0);add(i+n,s,0,0);
    if(i!=n)
        add(i+n,i+1+n,1e9,0),add(i+1+n,i+n,0,0);
    if(i+b<=n)
        add(i+n,i+b,1e9,c),add(i+b,i+n,0,-c);
    if(i+d<=n)
        add(i+n,i+d,1e9,e),add(i+d,i+n,0,-e);
}