坐标转换原理

一、坐标转换描述

坐标转换是空间实体的位置描述，是从一种坐标系统变换到另一种坐标系统的过程。通过建立两个坐标系统之间一一对应关系来实现。通常坐标转换有平移、缩放、旋转三个方面的转换。本文只详细讲述关于旋转部分的内容。

二、二维坐标旋转

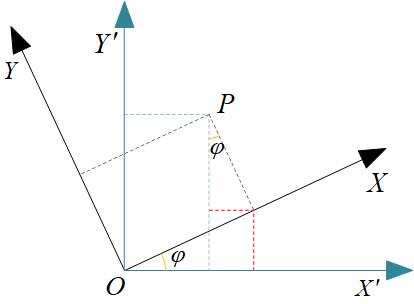
一个二维坐标系O-XY绕原点O旋转$\varphi $后变为另一个坐标系O-X'Y'。假设有一点P在O-XY坐标系下的坐标为（x,y），经旋转后在O-X'Y'坐标系下的坐标为（x',y'），则两套坐标系下的坐标的对应关系为

 $\left\{\begin{matrix} x^{'}=xcos\varphi-ysin\varphi\\y^{'}=xsin\varphi+ycos\varphi \end{matrix}\right.$

将其写成矩阵形式为

$\begin{bmatrix}x^{'}\\ y^{'}\end{bmatrix}=\begin{bmatrix}cos\varphi & -sin\varphi\\ sin\varphi & cos\varphi \end{bmatrix}\begin{bmatrix}x\\ y\end{bmatrix}$ 

三、三维坐标旋转

三维坐标转换主要分为右手系（笛卡尔坐标系）和左手系（测量坐标系）两种，其分别绕Z、Y、X顺时针旋转$\kappa,\omega,\varphi $角度。现在来看一看各轴旋转后坐标的变化。

1、绕Z轴旋转

              

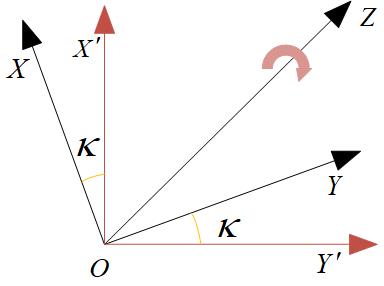
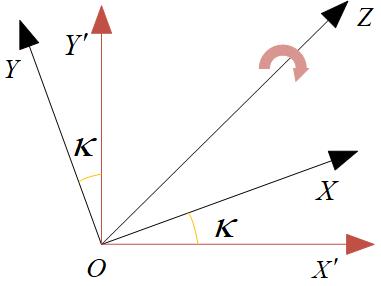
右：$\begin{bmatrix}x^{'}\\ y^{'}\\ z^{'}\end{bmatrix}=\begin{bmatrix} cos\kappa&sin\kappa&0\\-sin\kappa&cos\kappa&0\\0&0&1\\ \end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}$ 左：$\begin{bmatrix}x^{'}\\ y^{'}\\ z^{'}\end{bmatrix}=\begin{bmatrix} cos\kappa  & -sin\kappa  & 0\\sin\kappa  & cos\kappa & 0\\ 0 & 0 &1\\ \end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}$ 

2、绕Y轴旋转

          

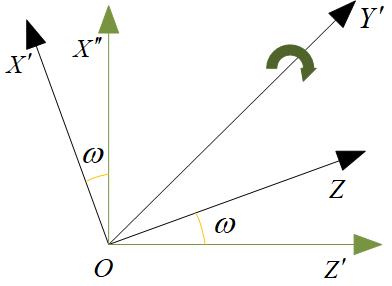
右：$\begin{bmatrix}x^{''}\\ y^{''}\\ z^{''}\end{bmatrix}=\begin{bmatrix} cos\omega &0&-sin\omega \\0&1&0\\sin\omega&0 &cos\omega \\ \end{bmatrix}\begin{bmatrix}x^{'}\\ y^{'}\\ z^{'}\end{bmatrix}$ 左：$\begin{bmatrix}x^{''}\\ y^{''}\\ z^{''}\end{bmatrix}=\begin{bmatrix} cos\omega &0&sin\omega \\0&1&0\\-sin\omega&0 &cos\omega\end{bmatrix}\begin{bmatrix}x^{'}\\ y^{'}\\ z^{'}\end{bmatrix}$

3、绕X轴旋转

          

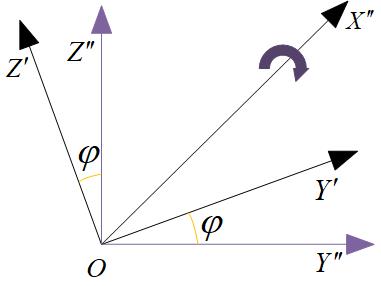
 右：$\begin{bmatrix}x^{'''}\\ y^{'''}\\ z^{'''}\end{bmatrix}=\begin{bmatrix}1 & 0 & 0\\ 0 & cos\varphi  & sin\varphi\\0 & -sin\varphi & cos\varphi\\ \end{bmatrix}\begin{bmatrix}x^{''}\\ y^{''}\\ z^{''}\end{bmatrix}$左：$\begin{bmatrix}x^{'''}\\ y^{'''}\\ z^{'''}\end{bmatrix}=\begin{bmatrix}1 & 0 & 0\\ 0 & cos\varphi  & -sin\varphi\\0 & sin\varphi & cos\varphi\\ \end{bmatrix}\begin{bmatrix}x^{''}\\ y^{''}\\ z^{''}\end{bmatrix}$

4、旋转矩阵融合

将三轴的旋转融合为一个旋转矩阵R 。

右：$\begin{bmatrix}x^{'''}\\ y^{'''}\\ z^{'''}\end{bmatrix}=\begin{bmatrix}1 & 0 & 0\\ 0 & cos\varphi  & sin\varphi\\0 & -sin\varphi & cos\varphi\\ \end{bmatrix}\begin{bmatrix} cos\omega &0&-sin\omega \\0&1&0\\sin\omega&0 &cos\omega \\ \end{bmatrix}\begin{bmatrix} cos\kappa&sin\kappa&0\\-sin\kappa&cos\kappa&0\\0&0&1\\ \end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}=\begin{bmatrix}r_{11} & r_{12} & r_{13}\\ r_{21} & r_{22} & r_{23}\\ r_{31} & r_{32} & r_{33}\end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}$

左：$\begin{bmatrix}x^{'''}\\ y^{'''}\\ z^{'''}\end{bmatrix}=\begin{bmatrix}1 & 0 & 0\\ 0 & cos\varphi  & -sin\varphi\\0 & sin\varphi & cos\varphi\\ \end{bmatrix}\begin{bmatrix} cos\omega &0&sin\omega \\0&1&0\\-sin\omega&0 &cos\omega\end{bmatrix}\begin{bmatrix} cos\kappa  & -sin\kappa  & 0\\sin\kappa  & cos\kappa & 0\\ 0 & 0 &1\\ \end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}=\begin{bmatrix}r_{11} & r_{12} & r_{13}\\ r_{21} & r_{22} & r_{23}\\ r_{31} & r_{32} & r_{33}\end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}$

 右手坐标系得旋转矩阵R的各个元素为

$\left\{\begin{matrix}r_{11}=cos\omega cos\kappa &r_{12}=cos\omega sin\kappa &r_{13}=-sin\omega \\ r_{21}=-cos\varphi sin\kappa +sin\varphi sin\omega cos\kappa & r_{22}=cos\varphi cos\kappa +sin\varphi sin\omega sin\kappa &r_{23}=sin\varphi cos\omega \\ r_{31}=sin\varphi sin\kappa +cos\varphi sin\omega cos\kappa&r_{32}=-sin\varphi cos\kappa +cos\varphi sin\omega sin\kappa&r_{33}=cos\varphi cos\omega \end{matrix}\right.$

 左手坐标系得旋转矩阵R的各个元素为

$\left\{\begin{matrix}r_{11}=cos\omega cos\kappa &r_{12}=-cos\omega sin\kappa &r_{13}=sin\omega \\ r_{21}=cos\varphi sin\kappa +sin\varphi sin\omega cos\kappa & r_{22}=cos\varphi cos\kappa -sin\varphi sin\omega sin\kappa &r_{23}=-sin\varphi cos\omega \\ r_{31}=sin\varphi sin\kappa -cos\varphi sin\omega cos\kappa&r_{32}=sin\varphi cos\kappa +cos\varphi sin\omega sin\kappa&r_{33}=cos\varphi cos\omega \end{matrix}\right.$