【知识点】树链剖分中的重链剖分
前言
需要先了解:
线段树(如果你会写线段树,也可以忽略(如果你不屑于学线段树,也可以忽略~))
定义
树链剖分:将一棵树化简成一条线段,用维护线段的数据结构(常见的有树状数组、ST表、线段树等)去维护这棵树。
树链剖分,最常见重链剖分和长链剖分两种,本文讲重链剖分。
首先,明确我们需要解决什么问题:洛谷-重链剖分模板题。
现在,我们需要快速地维护某个节点到另一个节点的简单路径上的所有权值,也要快速维护一棵子树的所有权值。那么,如果我们把树拆成线段,它们应该是相邻,或大面积相邻的。这样方便维护。
接下来给出一些可能会用到的定义:
重儿子:以该儿子为根节点时子树的节点数量最多,那么该儿子为重儿子(当有两棵以上以不同儿子为根节点的子树,它们的节点数量相等时,任选一个当重儿子都行)。
轻儿子:除了重儿子,其他儿子都是轻儿子。
顶点:某条重链开始的点,也是这条重链中深度最小的(最接近根节点的)。
重链:从顶点开始,选取重儿子,然后选择重儿子的重儿子……一路上只选择重儿子,直到叶子节点。
重链剖分
过程
DFS。从根节点开始,每次找重儿子接上,直到叶子节点,得到一条重链。途中会经过某些点有轻儿子,那么以它们的轻儿子为顶点,延申出新的重链。这棵树就会被剖分成多条重链。
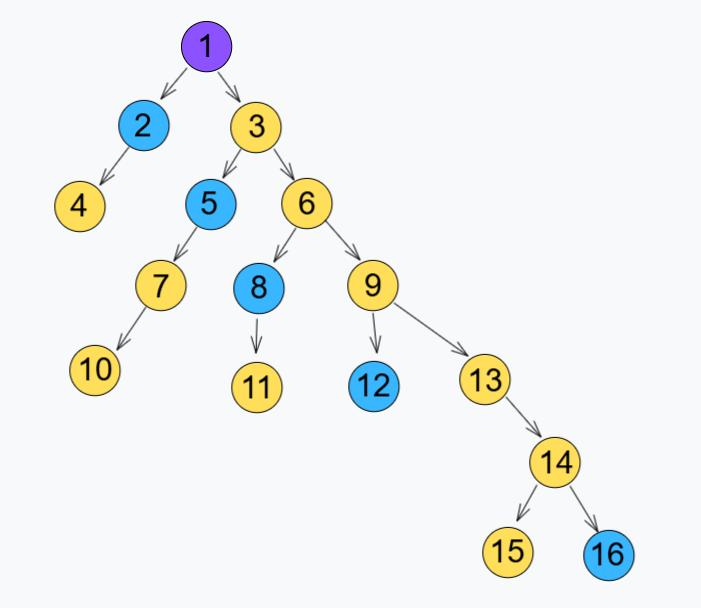
如图,紫色为根节点,黄色为重儿子,蓝色为轻儿子。我们需要按照上述顺序构建重链。
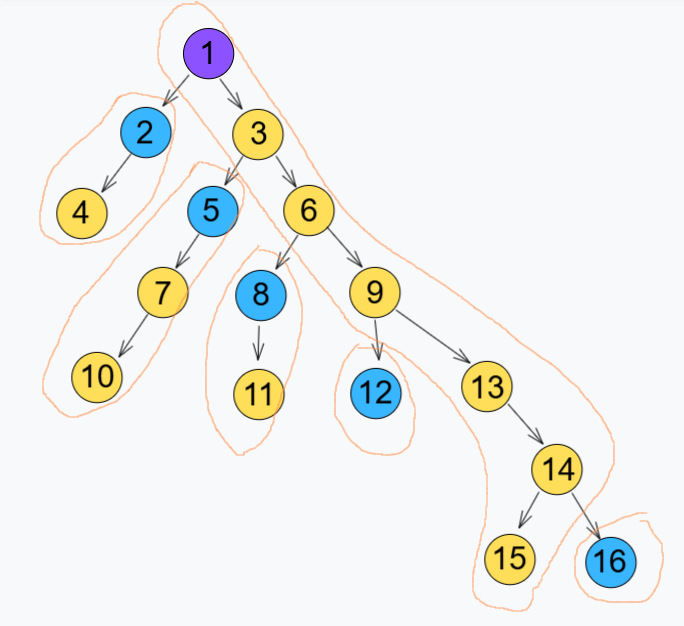
如图,棕色圈出来的就是一条重链,我们成功将上面这棵树剖分成了六条重链。每条重链的顶点是一个轻儿子或者根节点。但是,这样的节点序号并不符合我们的需要,我们需要新的节点序号!按照构建重链时的DFS顺序,依次为以上节点编号。
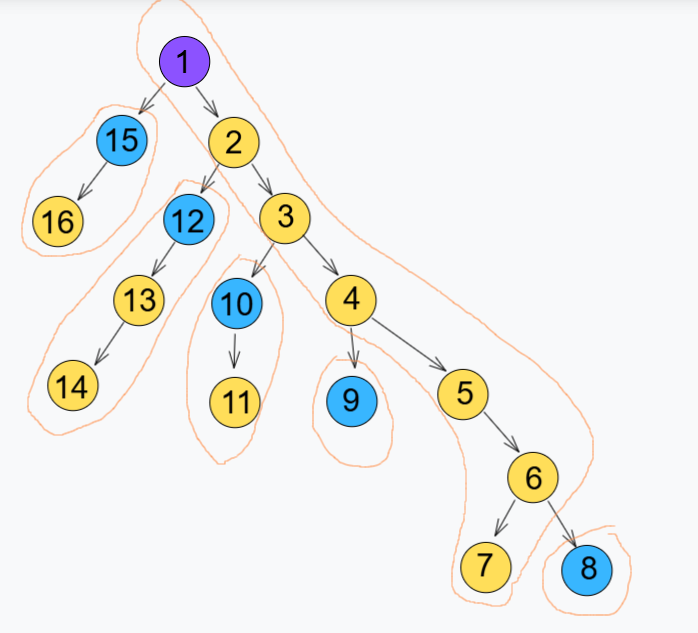
实现
直接DFS,我们并不知道哪些是重儿子,而且很多信息(比如子树大小)都不确定。所以我们需要两次DFS,第一次收集每个节点的深度、父节点编号、子树大小、重儿子编号这些信息,第二次再重新编号并树链剖分。这个重新编的新序号就是在线性数据结构(线段树)等中维护的目标。
void dfs1(i64 now, i64 fa, i64 deep) {
//第一次dfs,统计树上信息
fat[now] = fa;
dep[now] = deep;
siz[now] = 1;
for (auto v : edge[now]) {
if (v == fa)
continue;
dfs1(v, now, deep + 1);
siz[now] += siz[v];
if (siz[v] > siz[son[now]])
son[now] = v;
}
return;
}
void dfs2(i64 now, i64 ttop) { //ttop表示当前重链的顶点
//第二次dfs,重链剖分
id[now] = cnt; //cnt是节点编号
f_id[cnt] = now; //反着也要记录上,待会儿有用
cnt++;
top[now] = ttop; //记得记录这个节点所在链的顶点,有用
if (!son[now]) //到叶子节点结束
return;
dfs2(son[now], ttop); //重儿子接上
for (auto v : edge[now]) { //轻儿子单独成重链顶点
if (v == fat[now] || v == son[now])
continue;
dfs2(v, v);
}
return;
}
重链应用
过程-简单路径
有了以上重链,我们该如何实现某个简单路径的查询呢?比如说从\(10\)节点到\(14\)节点,路径为\(10->7->5->3->6->9->13->14\),怎么更改或者查询整条路径呢?首先,查询这两个节点的顶点所在链顶点(刚刚记录过)。
如果是同一个顶点,那这两个点在同一重链中。同一重链中,新序号是连续的,那么只需要更改或查询这一段连续新序号,就能完成目标。
但\(10\)所在链顶点是\(5\),\(14\)所在链顶点是\(1\),不相同。怎么办呢?比较谁的顶点的深度(刚刚也记录过)更大(离根节点远),谁就是\(x\)。这里假设\(x\)是\(10\)。那么从\(x\)到\(x\)的顶点,即\(10\)到\(5\)这段区间需要被更新或查询,这是同一重链内的,新编号连续。(新编号为从\(12\)到\(14\))然后,将\(x\)变为\(x\)所在链顶点的父节点。\(5\)的父节点是\(3\),现在\(x\)是\(3\)了。
现在相当于要处理\(3\)到\(14\)这段区间,我们发现它们所在链顶点都为\(1\),那么处理\(3\)到\(14\)即可。如果顶点仍然不同,需要再次找\(x\),变化\(x\),进行处理。所以上面操作要用while循环来完成。
实现-简单路径
//更新或查询的区间为[x, y],更新的值为z
void upd1() {
z %= MOD; //取模别忘了
while (top[x] != top[y]) {
//分段更新
if (dep[top[x]] < dep[top[y]]) //比较顶点深度,深的为x
swap(x, y);
ad(id[top[x]], id[x], z, 1, n, 1); //更新函数(此题要用线段树,这是线段树部分的代码)
x = fat[top[x]];
}
if (dep[x] > dep[y])
swap(x, y);
ad(id[x], id[y], z, 1, n, 1); //最后同一条链内依然更新
return;
}
void q1() {
i64 ans = 0; //记录答案
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]])
swap(x, y);
ans = (ans + query(id[top[x]], id[x], 1, n, 1)) % MOD;
x = fat[top[x]];
}
if (dep[x] > dep[y])
swap(x, y);
ans = (ans + query(id[x], id[y], 1, n, 1)) % MOD;
cout << ans << '\n';
return;
}
过程-子树
观察上面的新编号,大声告诉我你发现了什么?
没错,同一棵子树内,新编号都是连续的,而且根节点是最小的那个。那就很简单了,假设要处理以\(x\)为根的子树,我们已经记录了以\(x\)为根的子树的大小\(siz_x\)和\(x\)的新编号\(id_x\),那么整棵子树就是\([id_x, id_x+siz_x-1]\),直接处理就行。
实现-子树
void upd2() {
z %= MOD; //依旧取模别忘了\.
ad(id[x], id[x] + siz[x] - 1, z, 1, n, 1);
return;
}
void q2() {
cout << query(id[x], id[x] + siz[x] - 1, 1, n, 1) << '\n';
return;
}
最终代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
i64 n, m, r, MOD;
i64 a[100100]; //各节点初始值
vector<i64>edge[100100]; //边集
i64 dep[100100]; //节点深度
i64 fat[100100]; //父节点编号
i64 id[100100]; //新编号
i64 f_id[100100]; //原编号
i64 top[100100]; //所在重链的顶端
i64 siz[100100]; //子树大小
i64 son[100100]; //重儿子
i64 d[400100]; //线段树维护对象(新编号下各节点值)
i64 add[400100]; //懒惰标记
i64 cnt = 1, x, y, z, opt;
void dfs1(i64 now, i64 fa, i64 deep) {
//第一次dfs,统计树上信息
fat[now] = fa;
dep[now] = deep;
siz[now] = 1;
for (auto v : edge[now]) {
if (v == fa)
continue;
dfs1(v, now, deep + 1);
siz[now] += siz[v];
if (siz[v] > siz[son[now]])
son[now] = v;
}
return;
}
void dfs2(i64 now, i64 ttop) {
//第二次dfs,重链剖分
id[now] = cnt;
f_id[cnt] = now;
cnt++;
top[now] = ttop;
if (!son[now])
return;
dfs2(son[now], ttop);
for (auto v : edge[now]) {
if (v == fat[now] || v == son[now])
continue;
dfs2(v, v);
}
return;
}
void build(i64 s, i64 t, i64 p) {
if (s == t) {
d[p] = a[f_id[s]] % MOD;
return;
}
i64 mid = (s + t) / 2;
build(s, mid, 2 * p), build(mid + 1, t, 2 * p + 1);
d[p] = (d[2 * p] + d[2 * p + 1]) % MOD;
return;
}
void pushdown(i64 s, i64 t, i64 p) {
i64 mid = (s + t) / 2;
d[2 * p] = (d[2 * p] + (add[p] * (mid - s + 1)) % MOD) % MOD;
d[2 * p + 1] = (d[2 * p + 1] + (add[p] * (t - mid)) % MOD) % MOD;
add[2 * p] = (add[2 * p] + add[p]) % MOD;
add[2 * p + 1] = (add[2 * p + 1] + add[p]) % MOD;
add[p] = 0;
return;
}
void ad(i64 l, i64 r, i64 k, i64 s, i64 t, i64 p) {
if (l <= s && t <= r) {
d[p] = (d[p] + (k * (t - s + 1)) % MOD) % MOD;
add[p] = (add[p] + k) % MOD;
return;
}
i64 mid = (s + t) / 2;
pushdown(s, t, p);
if (l <= mid)
ad(l, r, k, s, mid, 2 * p);
if (r > mid)
ad(l, r, k, mid + 1, t, 2 * p + 1);
d[p] = (d[2 * p] + d[2 * p + 1]) % MOD;
return;
}
i64 query(i64 l, i64 r, i64 s, i64 t, i64 p) {
if (l <= s && t <= r)
return d[p];
i64 res = 0;
i64 mid = (s + t) / 2;
pushdown(s, t, p);
if (l <= mid)
res = (res + query(l, r, s, mid, 2 * p)) % MOD;
if (r > mid)
res = (res + query(l, r, mid + 1, t, 2 * p + 1)) % MOD;
return res;
}
void upd1() {
z %= MOD;
while (top[x] != top[y]) {
//分段更新
if (dep[top[x]] < dep[top[y]])
swap(x, y);
ad(id[top[x]], id[x], z, 1, n, 1);
x = fat[top[x]];
}
if (dep[x] > dep[y])
swap(x, y);
ad(id[x], id[y], z, 1, n, 1);
return;
}
void q1() {
i64 ans = 0;
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]])
swap(x, y);
ans = (ans + query(id[top[x]], id[x], 1, n, 1)) % MOD;
x = fat[top[x]];
}
if (dep[x] > dep[y])
swap(x, y);
ans = (ans + query(id[x], id[y], 1, n, 1)) % MOD;
cout << ans << '\n';
return;
}
void upd2() {
z %= MOD;
ad(id[x], id[x] + siz[x] - 1, z, 1, n, 1);
return;
}
void q2() {
cout << query(id[x], id[x] + siz[x] - 1, 1, n, 1) << '\n';
return;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m >> r >> MOD;
for (i64 i = 1; i <= n; i++)
cin >> a[i];
for (i64 i = 0; i < n - 1; i++) {
cin >> x >> y;
edge[x].push_back(y);
edge[y].push_back(x);
}
dfs1(r, 0, 1);
dfs2(r, r);
build(1, n, 1);
while (m--) {
cin >> opt;
if (opt == 1) {
cin >> x >> y >> z;
upd1();
} else if (opt == 2) {
cin >> x >> y;
q1();
} else if (opt == 3) {
cin >> x >> z;
upd2();
} else {
cin >> x;
q2();
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号