超立方体的有向链剖分

问题

将 \(0,1,\cdots,2^n-1\) 划分成尽量少的有向链，使得其中每一条路径 \(a_1\to a_2\to\cdots\to a_k\) 都满足 \(a_i<a_{i+1}\) 且 \(\operatorname{popcount}(a_i \oplus a_{i+1})=1\)。

分析

对于每个数，我们要么找到它的前驱，要么钦定它为链首。前驱一定是原数的二进制位中把一个 \(1\) 变成 \(0\)，因此我们考虑取哪个 \(1\)。

对于一个数 \(x\) 的二进制表示，把 \(0\) 看成左括号，\(1\) 看成右括号，进行括号匹配。我们选择最靠右的无法匹配的 \(1\)（若无符合条件的 \(1\) 则 \(x\) 为链首）。

接下来我们说明不会存在两个数前驱相同。为了方便描述，我们把数看成折线，从左到右考虑每一位，为 \(0\) 时向右下走，为 \(1\) 时向右上走。无法匹配的 \(1\) 需要满足它对应的线段左侧没有任何线段。

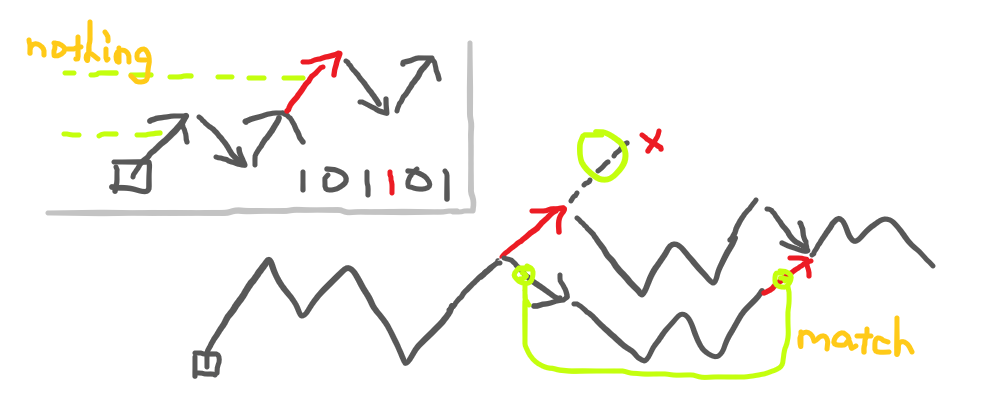
反证，假设两个数的前驱均为 \(z\)。我们用灰色折线表示 \(z\)，两条红色线段为这两个数删去的 \(1\)。假设左边那条红线段合法，那么它之后的灰色线段的高度不能超过它，否则它不是原数中最后一个合法的 \(1\)。因此，右边的红线段高度一定低于它。从而第二条红线段的左侧能找到匹配，导出矛盾。

还有一种证法。可以根据上述分析倒推出怎么求一个数的后继：我们把折线图左右翻转后跑同样的算法，就会找到原数中的一个 \(0\)，把它变成 \(1\) 就是原数的后继。当每个数的后继唯一确定，就不可能有两个数前驱相同了。

这种算法会产生 \(\binom{n}{\lfloor\frac{n}{2}\rfloor}\) 条有向链。这达到了下界，因为所有 popcount 为 \(\lfloor \frac{n}{2}\rfloor\) 的数必定属于不同的链。