P5458 [BJOI2016] 水晶

题目大意

给你一个三维平面坐标系，每个点的坐标用 \((x, y, z)\) 表示（描述分别从原点向三个轴各走了多少步），形如：

我们定义所有 \((x + y + z) \bmod 3 = 0\) 的点为能量源，形如：

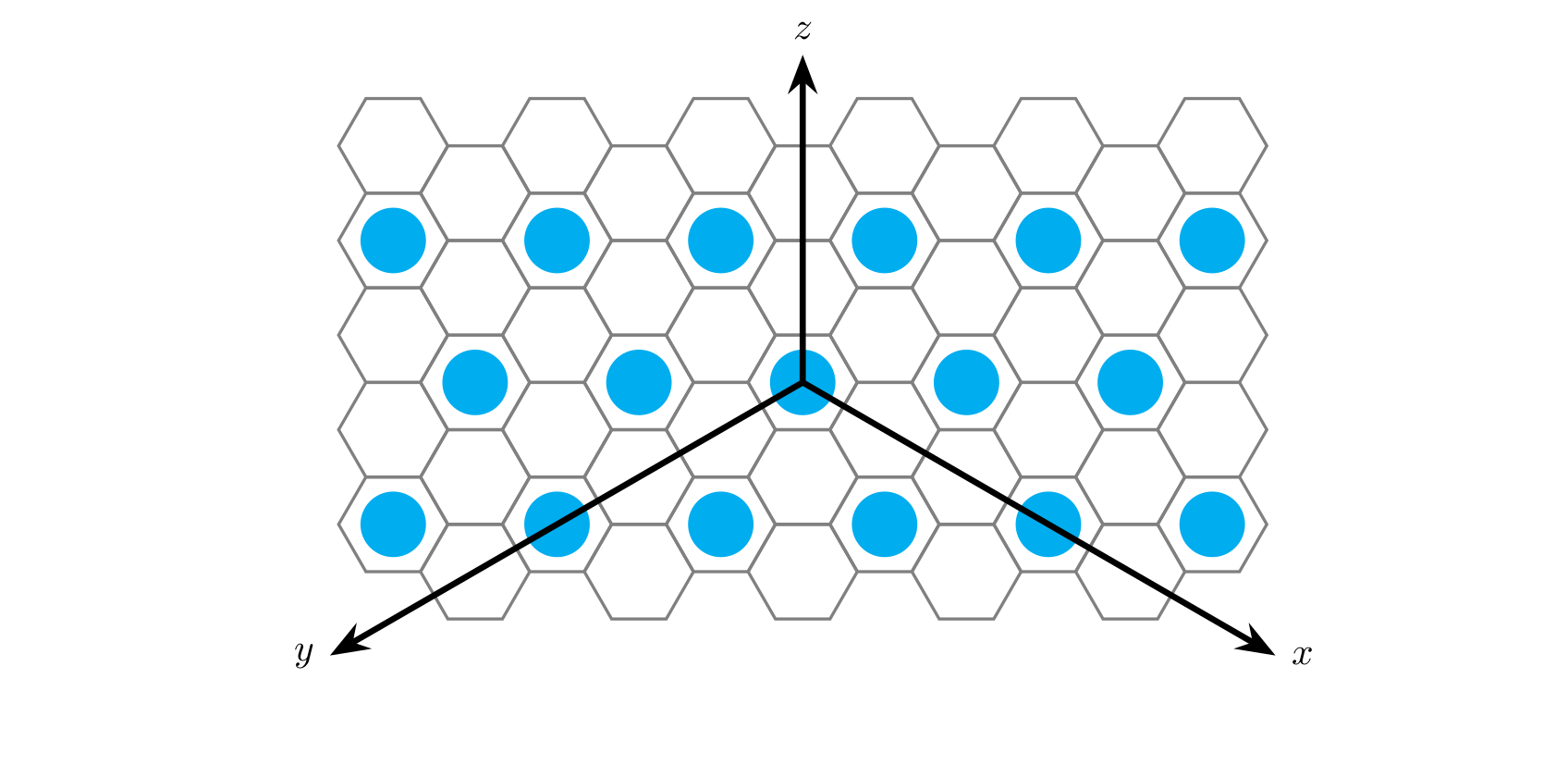
输入给你 \(n\) 块水晶，每块水晶都有一个价值 \(c_i\)，可能会在相同位置上，水晶满足某种关系时会产生共振，有两种共振如下：

• \(a\) 共振：三个格子组成三角形并且除了是能量源的格子上都有水晶。
• \(b\) 共振：三个格子组成一条线并且除了中间有能量源的格子上都有水晶。

要求炸掉一些水晶，使得剩余水晶没有共振且剩余水晶价值最大，输出最大价值。

\(1 \le n \le 50000, 1 \le 1000 \le c_i, -1000 \le x, y, z \le 1000\)。

题目思路

考虑一个格子可能有多种坐标表示，不好解决这个问题，不难想到将三维坐标转化成二维坐标，即 \((x - z, y - z)\)，这样每个格子的坐标表示形式就是唯一的了，而且可以形成一组双射。

那我们思考这个问题怎么做，发现炸掉一些水晶，没有共振，还要剩余水晶价值更大！这很难不让我们往最小割方面进行思考，考虑如何建图来表示 \(a, b\) 两种共振关系。我们发现，将以一个能量源为中心的周围 \(6\) 个格子进行黑白染色，发现 \(a, b\) 两种共振都是三个格子且除了能量源外的两个格子都不同色，这引发我们思考，往二分图的方面想。

我们发现，一个白点能把上述中的一个能量源外的 \(6\) 个格子的所有黑色格子上的水晶引发共振，所以我们其实可以用能量源来相互连接，而不是黑白点相互连接，准确的来说，这个东西就有点像三分图了，用 \((x + y + z) % 3\) 的三种值来对应三分图的三个部分，对于每个点，我们用拆点的方法来表示每个格子的水晶价值，然后用网络流跑最小割就好了。