常用的图像滤波算法解释
你想系统了解OpenCV中常用的图像滤波算法,包括它们的原理、数学公式、适用场景和代码实现,我会结合你小视场高精度图像处理的需求,从基础到进阶逐一讲解,让你清楚不同滤波算法的选择逻辑。
核心前提
图像滤波的核心目的是:保留有用信息(如边缘、细节)的同时,去除噪声(如高斯噪声、椒盐噪声)。根据滤波方式,可分为「线性滤波」和「非线性滤波」两大类,这也是理解所有滤波算法的基础。
一、线性滤波(基于卷积运算)
线性滤波的本质是卷积运算:用一个固定的卷积核(kernel)遍历图像,每个像素值等于自身和邻域像素值的加权和。优点是计算快、原理简单;缺点是会模糊边缘,对椒盐噪声效果差。
1. 均值滤波(Mean Filter)
原理
用像素邻域内所有像素的算术平均值替代当前像素值,是最简单的线性滤波。
- 卷积核(以3×3为例):
![image]()
适用场景
- 去除均匀分布的高斯噪声;
- 对图像进行轻度平滑,不追求边缘保留(不适合你的高精度测量场景)。
代码实现
#include <opencv2/opencv.hpp>
#include <iostream>
int main() {
cv::Mat img = cv::imread("noise_img.jpg"); // 读取含噪声的图像
if (img.empty()) {
std::cout << "无法读取图像" << std::endl;
return -1;
}
cv::Mat result;
// 均值滤波:参数1=输入图,参数2=输出图,参数3=卷积核尺寸(奇数)
cv::blur(img, result, cv::Size(3, 3));
cv::imshow("原图", img);
cv::imshow("均值滤波", result);
cv::waitKey(0);
return 0;
}
2. 高斯滤波(Gaussian Filter)
原理
对邻域像素加权平均,距离中心越近的像素权重越大(符合高斯分布),是最常用的线性滤波。
- 3×3高斯核(σ=1.5):
![image]()
适用场景
- 去除高斯噪声(最适配);
- 预处理(如边缘检测前的去噪);
- 你的小视场测量场景中,若图像有轻微高斯噪声,可先用高斯滤波去噪,不破坏细节。
代码实现
// 高斯滤波:参数4=X方向标准差(σ),参数5=Y方向标准差(默认和X相同)
cv::GaussianBlur(img, result, cv::Size(3, 3), 1.5);
3. 盒滤波(Box Filter)
原理
和均值滤波类似,但可选择是否归一化:
- 归一化:等价于均值滤波;
- 不归一化:计算邻域像素和(用于统计像素值总和)。
代码实现
// 盒滤波:参数4=归一化标志(true=均值滤波,false=求和)
cv::boxFilter(img, result, -1, cv::Size(3, 3), cv::Point(-1,-1), true);
二、非线性滤波(基于像素排序/自适应)
非线性滤波不依赖固定卷积核,而是根据邻域像素的分布特征(如排序、差异)计算输出,能更好保留边缘,适合你的高精度测量场景。
1. 中值滤波(Median Filter)
原理
用邻域像素的中位数替代当前像素值,是去除椒盐噪声的“黄金标准”。
- 示例:邻域像素值 [10, 200, 15, 12, 14],中位数是14,替代中心像素。
适用场景
- 去除椒盐噪声(黑白点噪声);
- 保留边缘(比线性滤波好);
- 你的小视场测量中,若标定板图像有椒盐噪声,优先用中值滤波。
代码实现
// 中值滤波:参数2=邻域尺寸(奇数)
cv::medianBlur(img, result, 3);
2. 双边滤波(Bilateral Filter)
原理
结合空间距离和像素值相似度的加权滤波:
- 空间距离:越近的像素权重越大(和高斯滤波一致);
- 像素值相似度:和中心像素值越接近,权重越大(避免模糊边缘)。
适用场景
- 去除噪声的同时保留边缘(如标定板边缘、测量目标边缘);
- 你的高精度测量场景首选(兼顾去噪和边缘保留)。
代码实现
// 双边滤波:
// 参数3=空间域核半径(越大覆盖范围越广)
// 参数4=像素值域标准差(越大,越容忍像素值差异)
// 参数5=边界处理方式
cv::bilateralFilter(img, result, 9, 75, 75);
3. 自适应中值滤波(Adaptive Median Filter)
原理
动态调整邻域尺寸:
- 若当前邻域的中位数是噪声(如椒盐点),扩大邻域;
- 直到找到非噪声的中位数,或达到最大邻域尺寸。
优势
比普通中值滤波更灵活,适合噪声密度变化的场景(OpenCV无内置函数,需自定义):
// 自定义自适应中值滤波(核心逻辑)
cv::Mat adaptiveMedianFilter(cv::Mat img, int maxKernelSize) {
cv::Mat result = img.clone();
int h = img.rows, w = img.cols;
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
int kernelSize = 3;
while (kernelSize <= maxKernelSize) {
// 提取邻域
int half = kernelSize / 2;
cv::Rect rect(std::max(0, j-half), std::max(0, i-half),
std::min(w-j-half, kernelSize), std::min(h-i-half, kernelSize));
cv::Mat roi = img(rect);
// 计算中位数
cv::Scalar medianVal = cv::median(roi);
// 判断是否为噪声(简化版:若当前像素和中位数差异大,扩大核)
if (abs(img.at<uchar>(i,j) - medianVal[0]) < 20) {
result.at<uchar>(i,j) = medianVal[0];
break;
}
kernelSize += 2;
}
}
}
return result;
}
4. 导向滤波(Guided Filter)
原理
基于引导图(通常是原图)的局部线性模型滤波,比双边滤波更快,边缘保留效果更好。
适用场景
- 高精度图像去噪、边缘保留;
- 标定图像的精细处理(需OpenCV contrib模块)。
三、滤波算法选择指南(针对你的场景)
| 噪声类型 | 推荐算法 | 核心优势 |
|---|---|---|
| 高斯噪声 | 高斯滤波/双边滤波 | 去噪+轻度保留边缘 |
| 椒盐噪声 | 中值滤波/自适应中值滤波 | 精准去噪,不模糊边缘 |
| 需保留测量边缘 | 双边滤波/导向滤波 | 去噪的同时最大化保留边缘细节 |
总结
- 线性滤波(均值/高斯):计算快,适合高斯噪声,但会模糊边缘;
- 非线性滤波(中值/双边):适合椒盐噪声,能保留边缘,是你的小视场高精度测量首选;
- 实际应用中,建议先尝试双边滤波(兼顾去噪和边缘),若有椒盐噪声则先用中值滤波预处理。



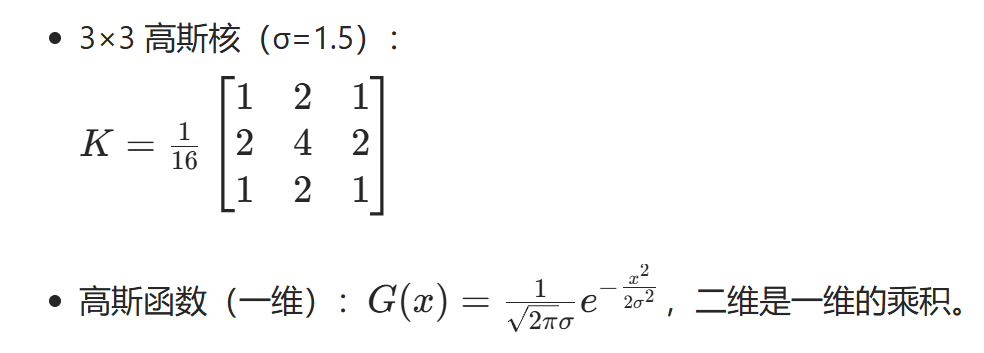

 浙公网安备 33010602011771号
浙公网安备 33010602011771号