在立体匹配环节,匹配代价计算的作用?
立体匹配中匹配代价计算的作用与原理
在立体匹配流程中,匹配代价计算(Matching Cost Computation) 是第一步核心操作,其作用是量化左右图像对应像素块的相似度,为后续的代价聚合、视差决策提供基础数据。简单来说:匹配代价越低,像素块的相似度越高,越可能是同一空间点的投影。
一、核心作用:从“像素对比”到“相似度量化”
立体匹配的本质是为左图每个像素 (u_l,v),在右图同一行的候选视差范围内,找到最相似的像素 (u_r,v)(u_r=u_l-d,d为候选视差)。
匹配代价计算的核心价值体现在3个层面:
- 建立相似度衡量标准
直接对比单个像素的灰度值容易受噪声、光照变化影响,因此需要以像素块(窗口) 为单位计算代价,利用邻域信息提升鲁棒性。 - 生成初始代价空间
对左图每个像素 (u_l,v) 和每个候选视差 d,计算一个代价数值 C(u_l,v,d),最终形成三维代价空间(高度×宽度×视差范围)。 - 为后续步骤提供输入
初始代价空间是代价聚合(空间域平滑噪声)、视差决策(赢家通吃策略)的基础,代价计算的精度直接决定最终视差图的质量。
二、为什么需要“代价计算”?—— 解决单像素匹配的痛点
如果直接对比单个像素的灰度值,会面临3个关键问题:
| 单像素匹配的痛点 | 匹配代价计算的解决方案 |
|---|---|
| 对噪声敏感(如椒盐噪声、传感器噪声) | 以像素块为单位计算代价,通过邻域平均抑制噪声 |
| 对光照变化鲁棒性差(如阴影、曝光不均) | 采用归一化代价函数(如NCC),消除光照强度差异的影响 |
| 低纹理区域无法匹配(如纯色墙面) | 利用像素块的梯度信息(如Census变换),提取纹理特征 |
三、匹配代价计算的数学本质与流程
1. 数学定义

2. 工程实现流程
匹配代价计算的标准步骤如下:
-
图像预处理:将彩色图像转为灰度图,对图像进行高斯滤波(进一步抑制噪声);
-
确定候选视差范围:根据双目相机基线和测量距离,设定最小视差d_{min} 和最大视差 d_{max};
-
滑动窗口遍历:对左图每个像素 (x,y),遍历所有候选视差
![image]()
-
计算块代价:对每个窗口W内的像素对,代入代价函数计算代价数值;
-
构建代价空间:将所有C(x,y,d) 存储为三维数组,供后续步骤使用。
四、常见代价函数对比(原理+优缺点)
不同代价函数适用于不同场景,以下是工业界常用的4类代价函数:
| 代价函数 | 数学公式 | 核心原理 | 优点 | 缺点 |
|---|---|---|---|---|
| SAD(绝对误差和) | $C_{SAD}=\sum_ | I_l-I_r | $ | 计算窗口内像素灰度差的绝对值之和 |
| SSD(平方误差和) | 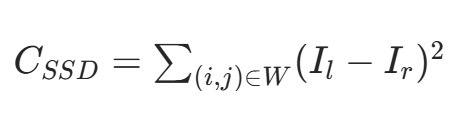 |
|||
| 计算窗口内像素灰度差的平方和 | 对差异大的像素惩罚更重,匹配精度略高于SAD | 计算量比SAD大,同样对光照敏感 | ||
| NCC(归一化互相关) | 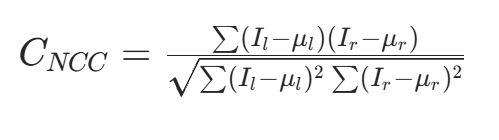 |
|||
| 计算两个窗口的灰度相关性,取值范围 $[-1,1]$,越接近1相似度越高 | 抗光照变化能力强,适合曝光不均的场景 | 计算量较大,需要预先计算窗口均值和方差 | ||
| Census变换 | 1. 对每个像素,生成二进制比特串(比较中心像素与邻域像素的大小) 2. 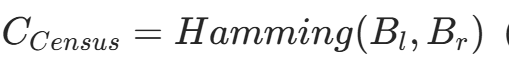 |
|||
| (比特串的汉明距离) | 基于像素邻域的相对灰度关系,而非绝对灰度值 | 抗光照、噪声能力极强,适合低纹理区域 | 计算复杂度高,需要额外存储比特串 |
工程选型建议:
- 实时性优先(如自动驾驶、机器人导航):选 SAD/SSD,结合CUDA并行加速;
- 精度优先(如三维建模、测绘):选 NCC/Census,牺牲部分速度换取鲁棒性;
- 平衡速度与精度:选 SGM算法默认的SAD代价,通过后续代价聚合提升精度。
五、与后续步骤的关联(代价计算→代价聚合→视差决策)
匹配代价计算是立体匹配的“起点”,但初始代价空间存在大量噪声(如单个像素噪声导致的代价波动),必须结合后续步骤才能得到可靠视差:
- 代价聚合:对初始代价空间进行空间域平滑(如动态规划、置信传播、SGM的路径聚合),让相邻像素的代价趋于一致,抑制噪声;
- 视差决策:采用赢家通吃(WTA) 策略,对每个像素 $(x,y)$,选择代价最小的候选视差
![image]()
作为最终视差; - 后处理:通过左右一致性检查、亚像素插值等优化视差图。
三者的关系:

六、C++/OpenCV 实现SAD代价计算示例
以下是手动实现SAD代价计算的核心代码,帮助理解底层逻辑:
#include <opencv2/opencv.hpp>
#include <vector>
using namespace cv;
using namespace std;
// 计算SAD匹配代价
// 参数:校正后的左右灰度图、窗口大小、视差范围
// 返回:三维代价空间(height × width × max_disp)
vector<Mat> computeSADCost(const Mat& imgL, const Mat& imgR, int windowSize, int maxDisp) {
CV_Assert(imgL.type() == CV_8U && imgR.type() == CV_8U);
CV_Assert(imgL.size() == imgR.size());
int height = imgL.rows;
int width = imgL.cols;
int halfWin = windowSize / 2;
// 初始化代价空间:每个视差对应一个代价图
vector<Mat> costSpace(maxDisp, Mat::zeros(height, width, CV_32S));
// 遍历每个像素(跳过边界)
for (int y = halfWin; y < height - halfWin; y++) {
for (int x = halfWin; x < width - halfWin; x++) {
// 遍历每个候选视差
for (int d = 0; d < maxDisp; d++) {
int xR = x - d; // 右图对应像素
if (xR < halfWin || xR >= width - halfWin) {
costSpace[d].at<int>(y, x) = INT_MAX; // 超出边界,代价设为极大值
continue;
}
// 计算窗口内的SAD值
int sad = 0;
for (int dy = -halfWin; dy <= halfWin; dy++) {
for (int dx = -halfWin; dx <= halfWin; dx++) {
uchar valL = imgL.at<uchar>(y + dy, x + dx);
uchar valR = imgR.at<uchar>(y + dy, xR + dx);
sad += abs(valL - valR);
}
}
costSpace[d].at<int>(y, x) = sad;
}
}
}
return costSpace;
}
// 赢家通吃策略生成视差图
Mat computeDisparityWTA(const vector<Mat>& costSpace) {
int height = costSpace[0].rows;
int width = costSpace[0].cols;
int maxDisp = costSpace.size();
Mat dispMap = Mat::zeros(height, width, CV_16S);
for (int y = 0; y < height; y++) {
for (int x = 0; x < width; x++) {
int minCost = INT_MAX;
int bestDisp = 0;
// 找到最小代价对应的视差
for (int d = 0; d < maxDisp; d++) {
int cost = costSpace[d].at<int>(y, x);
if (cost < minCost) {
minCost = cost;
bestDisp = d;
}
}
dispMap.at<short>(y, x) = bestDisp;
}
}
return dispMap;
}
int main() {
Mat imgL = imread("rect_left.png", IMREAD_GRAYSCALE);
Mat imgR = imread("rect_right.png", IMREAD_GRAYSCALE);
int windowSize = 5; // 5×5匹配窗口
int maxDisp = 16; // 最大视差
// 1. 计算SAD代价空间
vector<Mat> costSpace = computeSADCost(imgL, imgR, windowSize, maxDisp);
// 2. 赢家通吃生成视差图
Mat dispMap = computeDisparityWTA(costSpace);
// 3. 可视化
Mat disp8u;
normalize(dispMap, disp8u, 0, 255, NORM_MINMAX, CV_8U);
imshow("SAD视差图", disp8u);
waitKey(0);
return 0;
}
七、关键优化技巧
- 边界处理:对图像边界像素(窗口超出图像范围),将代价设为极大值,避免无效匹配;
- 积分图加速SAD/SSD:利用积分图可将窗口代价计算复杂度从 $O(w^2)$ 降至 $O(1)$($w$ 为窗口大小),大幅提升计算速度;
- 金字塔分层计算:先在低分辨率图像上计算代价,得到粗略视差,再在高分辨率图像上细化,减少候选视差范围;
- CUDA并行化:代价计算的嵌套循环适合并行处理,通过CUDA对每个像素-视差对并行计算,速度提升100倍以上。


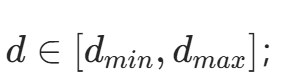
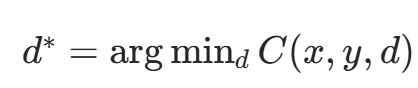

 浙公网安备 33010602011771号
浙公网安备 33010602011771号