什么是李代数

李代数（Lie Algebra）：从通俗理解到数学本质（三维重建视角）

李代数是连接连续群与线性空间的桥梁，在三维重建、SLAM、机器人运动学等领域中，核心作用是处理旋转/位姿的连续变换，解决旋转矩阵（正交约束）带来的优化难题。

本文延续「通俗解释→数学定义→工程应用」的递进逻辑，重点结合相机位姿优化场景讲解李代数的价值。

一、通俗解释：为什么需要李代数？

在光束平差（BA）或SLAM中，我们需要优化相机位姿（旋转 $R$ + 平移 $t$），但直接优化旋转矩阵会遇到两个「坑」：

1. 旋转矩阵的约束
   

2. 变换的连续性
   相机的运动是连续的（比如从位姿1平滑移动到位姿2），旋转矩阵描述的是「最终姿态」，但无法直接描述「姿态的变化量」（即「增量旋转」）。

李代数的核心思想：

为旋转群（或位姿群）找到一个对应的线性空间，在这个线性空间中可以无约束地进行加减、求导、优化，优化完成后再映射回旋转群（得到合法的旋转矩阵）。

打个比方：

二、数学基础：群与李群

理解李代数前，必须先掌握李群（Lie Group）——李代数是李群的「伴生结构」。

2.1 群（Group）：代数结构的定义

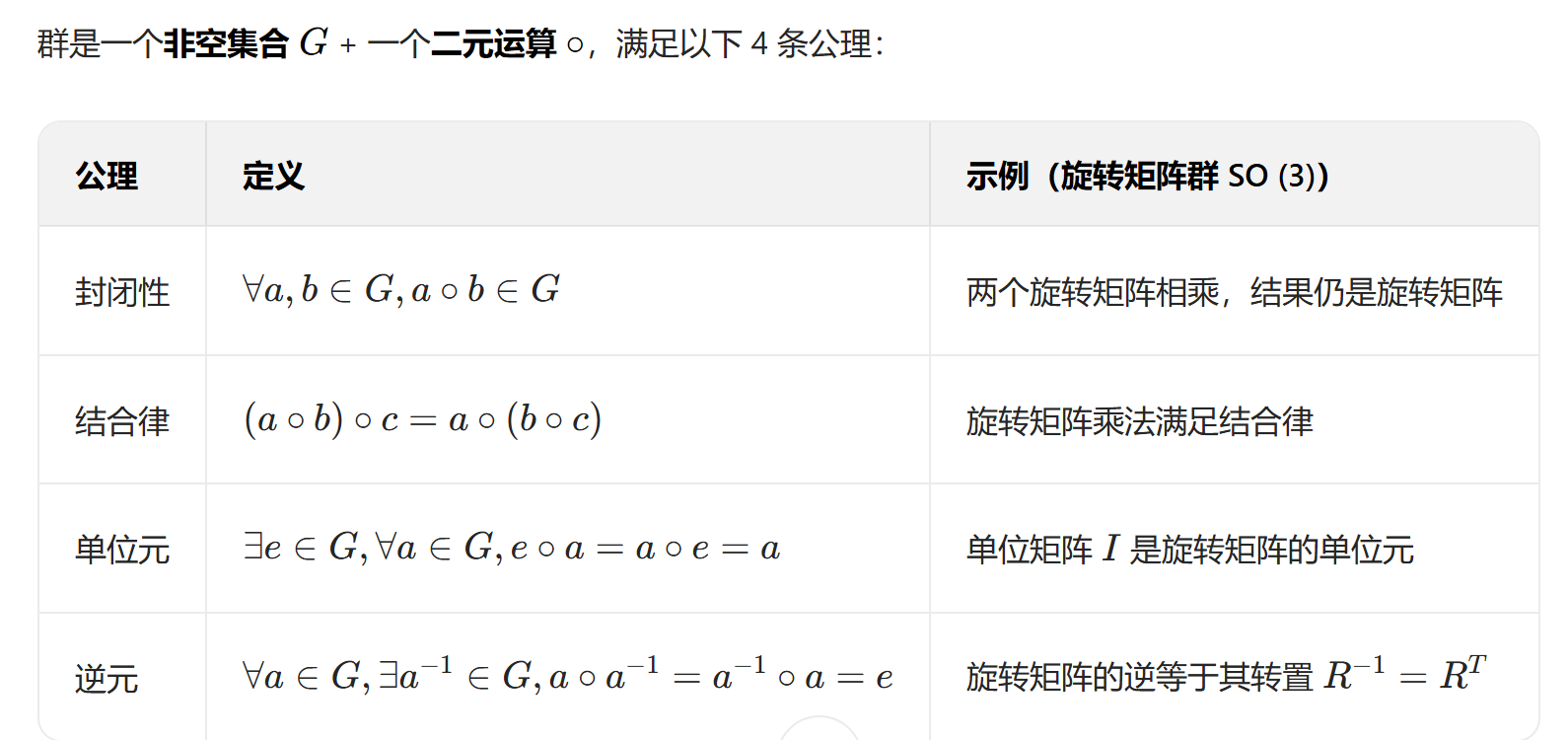
2.2 李群（Lie Group）：连续的群

李群是既是群，又是光滑流形的结构——通俗说，就是群中的元素是连续变化的。

在三维重建中，最常用的两个李群：

李群的痛点：元素是矩阵，满足非线性约束，无法直接进行微分和优化。

三、李代数的定义：李群的「线性化工具」

3.1 核心定义

这句话的关键是两个概念：

1. 切空间：在李群的单位元（比如SO(3)的单位矩阵$I$）上，所有「相切方向」构成的线性空间——这个空间是无约束的向量空间，可以自由进行加减、数乘、求导。
2. 李括号：定义在切空间上的二元运算，描述两个向量的「非交换性」（对应李群中元素乘法的非交换性，比如三维旋转不满足交换律）。

3.2 三维重建中常用的李代数

具体公式：

1. 指数映射（李代数→旋转矩阵）
   

2. 对数映射（旋转矩阵→李代数）
   

（2） 位姿李代数 $\mathfrak{se}(3)$

3.3 李括号运算

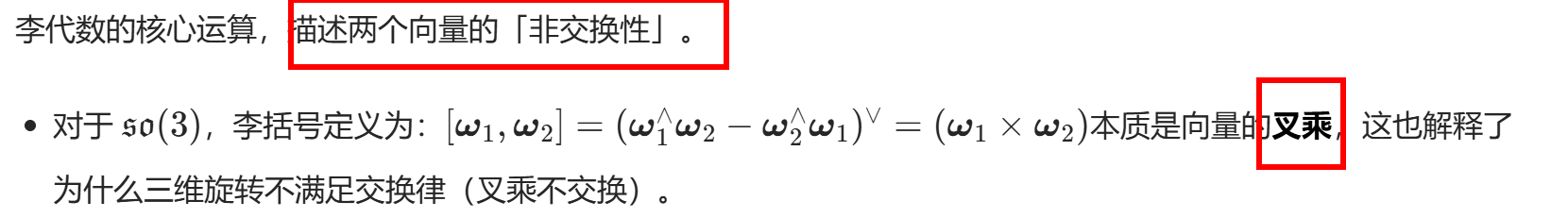
四、李代数的核心价值：解决优化中的约束问题

在光束平差（BA）中，优化相机位姿时，李代数的作用体现在两个核心场景：

4.1 无约束优化相机位姿

4.2 高效计算导数（扰动模型）

在BA中，需要计算重投影误差关于相机位姿的导数（雅可比矩阵），李代数的扰动模型可以大幅简化求导过程。

以旋转为例：

五、工程实现：李代数的代码应用（C++/Eigen）

在实际开发中，通常不需要手动实现指数/对数映射，可使用Sophus库（专为李代数设计的C++库，基于Eigen）。

5.1 安装Sophus

Sophus支持SO(3)和SE(3)的李代数运算，可通过源码编译安装：

git clone https://github.com/strasdat/Sophus.git
cd Sophus && mkdir build && cd build
cmake .. && make -j4

5.2 核心代码示例

#include <iostream>
#include <Eigen/Core>
#include <sophus/se3.hpp>

int main() {
    // 1. 定义旋转矩阵 R（绕z轴旋转90度）
    double theta = M_PI / 2;
    Eigen::Matrix3d R;
    R << cos(theta), -sin(theta), 0,
         sin(theta), cos(theta), 0,
         0, 0, 1;

    // 2. 旋转矩阵 → 李代数 so(3)
    Sophus::SO3d SO3_R(R); // 李群 SO(3)
    Eigen::Vector3d so3 = SO3_R.log(); // 对数映射 → 李代数向量
    std::cout << "so3 = " << so3.transpose() << std::endl;
    // 输出: so3 = 0 0 1.5708 （对应绕z轴旋转π/2）

    // 3. 李代数 → 旋转矩阵（指数映射）
    Sophus::SO3d SO3_so3 = Sophus::SO3d::exp(so3);
    std::cout << "R from so3 = \n" << SO3_so3.matrix() << std::endl;

    // 4. 位姿李代数 se(3) 示例
    Eigen::Vector3d t(1, 0, 0); // 平移向量
    Sophus::SE3d SE3_Rt(R, t); // 李群 SE(3)
    Eigen::Vector6d se3 = SE3_Rt.log(); // 对数映射 → 六维李代数向量
    std::cout << "se3 = " << se3.transpose() << std::endl;
    // 输出: se3 = 1 0 0 0 0 1.5708 （前3维平移，后3维旋转）

    // 5. 小扰动模型（计算雅可比常用）
    Eigen::Vector3d delta_omega(0.01, 0, 0); // 微小旋转增量
    Sophus::SO3d SO3_delta = Sophus::SO3d::exp(delta_omega);
    Sophus::SO3d SO3_new = SO3_R * SO3_delta; // 旋转更新
    std::cout << "new R = \n" << SO3_new.matrix() << std::endl;

    return 0;
}

六、总结

概念	本质	形式	核心作用
李群 SO(3)/SE(3)	连续变换群（有约束）	矩阵	描述相机的旋转/位姿
李代数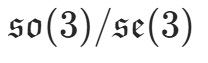
李群单位元的切空间（无约束）	向量（3维/6维）	优化位姿、计算导数
指数映射	切空间→李群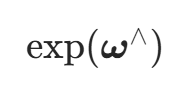
优化结果→合法矩阵
对数映射	李群→切空间	$\log(R)$	矩阵→优化变量

李代数的核心价值，是将有约束的矩阵优化问题，转化为无约束的向量优化问题，这也是它成为三维重建、SLAM领域基础工具的根本原因。