雅可比矩阵与海森矩阵(光束平差视角)
雅可比矩阵与海森矩阵(光束平差视角)
在光束平差(BA)及非线性优化领域,雅可比矩阵(Jacobian Matrix) 和海森矩阵(Hessian Matrix) 是核心数学工具。前者描述误差函数的局部线性变化率,是线性化非线性问题的关键;后者描述误差函数的二阶曲率,决定了迭代优化的步长和方向。
本文将从通俗解释→数学定义→BA中的具体形式→工程意义四个层面递进讲解,并结合BA的优化方程说明两者的作用。
一、通俗解释:矩阵到底在描述什么?
1.1 雅可比矩阵:「变化率的集合」

雅可比矩阵就是把所有自变量的偏导数「打包」,形成一个矩阵,用来描述 「输入变量的微小变化,会如何导致输出函数的变化」。
在BA中,输入是相机位姿和三维点坐标,输出是重投影误差。雅可比矩阵的作用就是量化:
相机位姿微调0.01弧度/厘米,或三维点坐标微调1毫米,重投影误差会变化多少像素?
1.2 海森矩阵:「曲率的集合」
还是爬山的例子:

海森矩阵是把所有二阶偏导数「打包」,形成一个对称矩阵,用来描述 「函数的局部曲率和变量间的耦合程度」。
在BA中,海森矩阵决定了优化迭代的步长:
曲率大(矩阵特征值大)→ 函数变化剧烈 → 步长要小,避免越过最优解;
曲率小(矩阵特征值小)→ 函数变化平缓 → 步长可以大,加快收敛。
二、数学定义:通用形式与维度分析
2.1 雅可比矩阵 J

关键性质
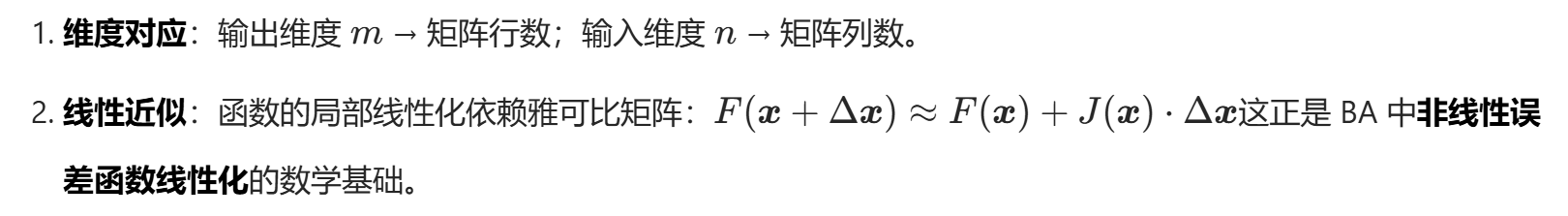
2.2 海森矩阵H

关键性质

三、BA中的具体形式:重投影误差的导数
在BA中,优化目标是最小化重投影误差的平方和:

3.1 BA中的雅可比矩阵 J

推导基础:重投影函数的链式求导
重投影函数 $f(\xi_i,P_j)$ 的计算流程为:

$$
工程上的简化计算

3.2 BA中的海森矩阵H

BA的核心优化方程

四、工程意义:为什么这两个矩阵对BA至关重要?
4.1 雅可比矩阵的作用
-
非线性问题线性化
BA的误差函数是高度非线性的(投影包含除法运算),无法直接求解。雅可比矩阵将误差函数在当前迭代点近似为线性函数,从而将优化问题转化为线性方程组求解(高斯-牛顿法的核心)。 -
稀疏性的根源
一个三维点只在少数相机中可见,因此每个![image]()
只与对应的相机和点相关。这导致整体雅可比矩阵J 是稀疏矩阵,进而海森矩阵 H 也是稀疏矩阵。
→ 工程上通过稀疏Schur消元(边缘化)大幅降低计算复杂度。 -
梯度方向的指引
雅可比矩阵的转置乘以误差向量![image]()
是误差函数的梯度,决定了迭代优化的方向:沿着梯度的反方向更新变量,可降低误差。
4.2 海森矩阵的作用
-
步长的自适应调整
![image]()
-
变量耦合关系的量化
海森矩阵的非对角块表示不同变量之间的耦合程度:![image]()
大 → 相机位姿和三维点坐标的耦合强,调整一个变量会显著影响另一个;- 稀疏性意味着耦合只存在于有观测关联的变量之间。
-
优化收敛性的判断
海森矩阵的正定性决定了优化算法的收敛性:- 若 $H$ 正定 → 迭代方向是下降方向,算法收敛;
- 若 $H$ 奇异 → 需加入阻尼项(LM法)或正则化,避免方程组无解。
五、代码层面的实现提示(C++/Eigen)
在BA的工程实现中,很少手动推导所有导数,通常结合自动求导或数值求导,但理解雅可比和海森的结构有助于优化性能:
- 手动推导关键导数:内参投影的导数($\frac{\partial f}{\partial P_c}$)可手动推导,减少自动求导的计算量;
- 稀疏矩阵存储:使用Eigen的
SparseMatrix存储雅可比和海森矩阵,避免稠密存储的内存爆炸; - Schur消元加速:利用
Eigen::SparseLU或第三方库(如CSparse)实现稀疏矩阵的分解与求解。
示例:手动计算内参投影的雅可比
// 输入:相机内参K,相机坐标系下的点P_c
// 输出:投影函数对P_c的雅可比矩阵J_proj (2x3)
Eigen::Matrix<double, 2, 3> compute_proj_jacobian(const Eigen::Matrix3d& K, const Eigen::Vector3d& P_c) {
double fx = K(0, 0), fy = K(1, 1);
double x = P_c(0), y = P_c(1), z = P_c(2);
double z_sq = z * z;
Eigen::Matrix<double, 2, 3> J;
J << fx / z, 0, -fx * x / z_sq,
0, fy / z, -fy * y / z_sq;
return J;
}
六、总结
| 矩阵 | 维度特征 | 核心作用 | BA中的关键价值 |
|---|---|---|---|
| 雅可比矩阵 | $m \times n$(输出×输入) | 描述函数局部线性变化率,实现非线性线性化 | 构建优化的线性方程组,决定梯度方向,支撑稀疏优化 |
| 海森矩阵 | $n \times n$(对称矩阵) | 描述函数局部曲率,量化变量耦合关系 | 决定迭代步长,判断收敛性,LM法的阻尼调整依据 |
雅可比矩阵是BA的「骨架」,支撑起非线性优化的线性化框架;海森矩阵是BA的「肌肉」,决定了优化迭代的效率和稳定性。两者结合,构成了光束平差算法的数学核心。
李代数的核心价值,是将有约束的矩阵优化问题,转化为无约束的向量优化问题,这也是它成为三维重建、SLAM 领域基础工具的根本原因。


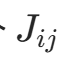
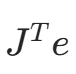

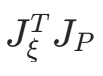

 浙公网安备 33010602011771号
浙公网安备 33010602011771号