讲解光束平差算法的原理和步骤
光束平差(Bundle Adjustment)算法原理与步骤
光束平差(Bundle Adjustment, BA)是三维重建、相机标定、视觉SLAM等领域的核心优化算法,本质是通过最小化重投影误差,联合优化相机位姿和三维点坐标,从而得到高精度的三维重建结果。
本文将遵循通俗解释→数学原理→算法步骤的递进逻辑,并结合实际应用场景讲解。
一、通俗解释:BA要解决什么问题?
在三维重建中(比如运动恢复结构SfM),我们通常通过以下步骤获取初始数据:
- 特征匹配:在不同图像中找到相同的特征点(比如角点)。
- 三角化:利用相机的初始位姿,通过多视图几何关系计算特征点对应的三维坐标。
但这两步会引入不可避免的误差:
- 相机位姿的初始估计(比如通过本质矩阵分解)存在误差;
- 特征点的提取和匹配存在噪声(比如光照变化、遮挡导致的匹配错误);
- 三角化得到的三维点坐标会被这些误差放大。
这些误差会导致一个问题:三维点投影回图像时,与实际观测的特征点位置不重合,这个偏差就是重投影误差。
光束平差的核心思想就是:调整相机的位姿和三维点的坐标,让所有三维点的重投影误差之和最小。
- 可以想象成:每个三维点向不同相机“发射光线”(光束),BA的目标是调整这些光束的方向和位置,让所有光束都精准“击中”图像上的观测特征点。
二、数学原理:BA的优化模型
2.1 核心概念定义


2.2 BA的优化目标

2.3 优化变量与约束
-
优化变量:分为两类
![image]()
-
约束:无显式约束,属于无约束优化问题。
三、算法步骤:BA的求解流程
BA的目标函数是非线性最小二乘问题,无法直接求解,通常采用迭代优化的方法,核心是高斯-牛顿法(Gauss-Newton) 或列文伯格-马夸尔特法(Levenberg-Marquardt, LM)。
3.1 核心思路:非线性问题线性化

其中:

3.2 BA的关键优化:稀疏性利用

-
![image]()
-
不同三维点之间没有直接关联,不同相机之间也没有直接关联。
利用稀疏性,可以将海森矩阵 H 分块为:

3.3 完整迭代步骤
-
初始化
- 输入:相机内参 $K$、特征匹配对、相机位姿初始值
![image]()
(由本质矩阵/基础矩阵分解得到)、三维点初始值![image]()
(由三角化得到)。 - 计算初始重投影误差
![image]()
,判断是否满足收敛条件(如误差小于阈值)。
- 输入:相机内参 $K$、特征匹配对、相机位姿初始值
-
线性化(迭代核心)
![image]()
-
求解增量方程
![image]()
-
更新参数
![image]()
-
收敛判断
- 计算更新后的重投影误差总和
![image]()
:- 若误差小于预设阈值,或迭代次数达到上限,停止迭代;
- 否则返回步骤2,进入下一次迭代。
- 计算更新后的重投影误差总和
四、BA的分类与应用场景
4.1 按优化变量分类
| 类型 | 优化变量 | 适用场景 |
|---|---|---|
| 稀疏BA | 相机位姿 + 三维点 | 运动恢复结构(SfM)、增量式SLAM |
| 稠密BA | 相机位姿 + 稠密三维点云 | 稠密重建(如COLMAP的稠密BA) |
| 单目BA | 单相机位姿 + 三维点 | 单目SLAM(如ORB-SLAM) |
4.2 工程实现关键点
- 雅可比矩阵的高效计算
雅可比矩阵的推导是BA实现的核心,需要结合李代数求导(避免旋转矩阵的正交约束),工程上通常预计算内参相关的导数,减少重复计算。 - 稀疏矩阵库的使用
直接使用稠密矩阵会导致内存爆炸,工程上常用CSparse、Eigen的稀疏模块或Ceres Solver(谷歌开源的非线性最小二乘库)处理稀疏矩阵。 - 鲁棒核函数
特征匹配中存在外点(错误匹配),会导致重投影误差过大,通常使用鲁棒核函数(如Huber核、Cauchy核)降低外点的权重,避免优化结果被外点主导。
五、代码实现思路(C++/Ceres Solver)
工程上很少手写BA的稀疏求解,通常使用Ceres Solver(支持自动求导+稀疏优化),核心步骤如下:
- 定义重投影误差代价函数
struct ReprojectionError { ReprojectionError(double observed_x, double observed_y, const Eigen::Matrix3d& K) : observed_x(observed_x), observed_y(observed_y), K(K) {} template <typename T> bool operator()(const T* const camera, const T* const point, T* residuals) const { // camera: 6维李代数(旋转3维+平移3维) // point: 3维世界坐标 T p_cam[3]; // 世界坐标→相机坐标 ceres::AngleAxisRotatePoint(camera, point, p_cam); p_cam[0] += camera[3]; p_cam[1] += camera[4]; p_cam[2] += camera[5]; // 相机坐标→像素坐标 T x = p_cam[0] / p_cam[2]; T y = p_cam[1] / p_cam[2]; T u = K(0,0)*x + K(0,2); T v = K(1,1)*y + K(1,2); // 重投影误差 residuals[0] = u - T(observed_x); residuals[1] = v - T(observed_y); return true; } double observed_x, observed_y; Eigen::Matrix3d K; }; - 构建优化问题并设置稀疏求解器
ceres::Problem problem; for (int i = 0; i < num_observations; ++i) { problem.AddResidualBlock( new ceres::AutoDiffCostFunction<ReprojectionError, 2, 6, 3>( new ReprojectionError(obs_x[i], obs_y[i], K)), new ceres::HuberLoss(1.0), // 鲁棒核函数 camera_params + 6*camera_id[i], // 相机位姿参数 point_params + 3*point_id[i] // 三维点参数 ); } // 配置稀疏求解器(使用Schur消元) ceres::Solver::Options options; options.linear_solver_type = ceres::SPARSE_SCHUR; options.minimizer_progress_to_stdout = true; ceres::Solver::Summary summary; ceres::Solve(options, &problem, &summary);
六、总结
- 核心目标:最小化重投影误差,联合优化相机位姿和三维点坐标。
- 数学本质:非线性最小二乘问题,通过迭代线性化(高斯-牛顿/LM)求解。
- 工程关键:利用稀疏性降低计算复杂度,使用鲁棒核函数处理外点,借助Ceres等库快速实现。
光束平差是三维重建的“灵魂算法”,其精度直接决定了重建结果的好坏,掌握BA的原理和实现是深入计算机视觉三维方向的必备基础。





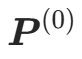
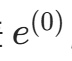


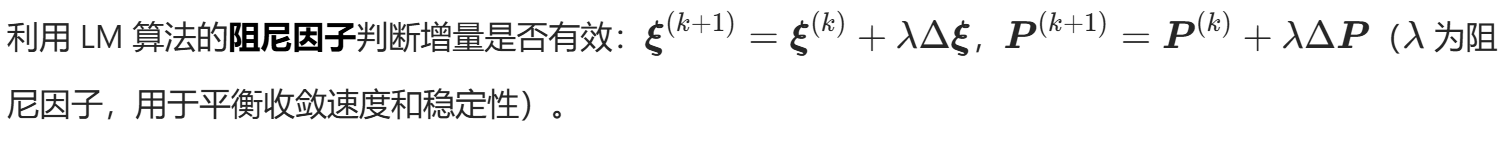


 浙公网安备 33010602011771号
浙公网安备 33010602011771号