双目中基础矩阵 / 本质矩阵啥意思
本质矩阵和基础矩阵描述了同一个三维场景在两个不同视角下的成像几何关系。它们是“双目视觉”和“运动恢复结构”的数学基石。
为了直观理解它们的定位与作用,我们可以先通过下面的流程图概览:
flowchart TD
A[同一三维场景] --> B[两个不同相机视角]
B --> C[两幅图像<br>(图像对)]
C --> D{已知相机参数?}
D -- 是<br>(已知内参K, K‘) --> E[使用“本质矩阵”E<br>描述几何关系]
E --> F[恢复纯旋转R与平移t]
D -- 否<br>(未知内参) --> G[使用“基础矩阵”F<br>描述更通用的几何关系]
G --> H[用于图像匹配/校正/重建的第一步]
F & H --> I[共同目标:<br>三维重建与场景理解]
核心思想:对极几何
想象你用左眼和右眼(两个相机)看同一个世界点 P。
- 你的左眼看到 P 在左视网膜(左图像)上的投影点是 p₁。
- 你的右眼看到 P 在右视网膜(右图像)上的投影点是 p₂。
对极几何研究的就是:已知 p₁,在另一张图像上寻找其对应点 p₂ 的约束关系。
这个约束就是:p₂ 必然位于由 p₁ 决定的一条直线上。这条线叫做 对极线。
本质矩阵(E)和基础矩阵(F)就是编码这个约束的数学矩阵。
1. 本质矩阵
定义:当你知道两个相机的内部参数(焦距、主点等,即内参矩阵 K)时,用来描述归一化坐标平面上对应点关系的矩阵。
-
作用场景:相机已标定(内参已知)。
-
数学形式:
![image]()
- 其中,( \mathbf{x}_1 ) 和 ( \mathbf{x}_2 ) 是三维点 P 在两个相机归一化成像平面上的坐标(即,将像素坐标用内参矩阵 K 的逆进行归一化,消除了焦距、主点等内部因素的影响)。
-
物理意义:本质矩阵 E 只包含了两个相机之间的相对运动信息—— 旋转 R 和 平移 t。
- 它由这两个量直接构成:( \mathbf{E} = [\mathbf{t}]_{\times} \mathbf{R} )
- 其中 ( [\mathbf{t}]_{\times} ) 是平移向量 t 的叉乘矩阵。
-
你能从E中得到什么:通过奇异值分解,可以从 E 中分解出4种可能的(R, t)组合,再通过三角化一点并检查其深度(为正)来得到唯一正确的解。这是从图像恢复相机运动的关键一步。
简单理解:本质矩阵是“纯净版”的关系,它剥离了相机自身特性(内参),只描述两个相机位置姿态的相对关系。
2. 基础矩阵
定义:一个更通用的矩阵,描述两个未标定相机的图像平面像素坐标之间对应点关系的矩阵。
-
作用场景:相机未标定(内参未知或不精确)。这是更常见、更实用的情况。
-
数学形式:
![image]()
- 其中,( \mathbf{p}_1 ) 和 ( \mathbf{p}_2 ) 是三维点 P 在两个图像上的像素坐标。
-
物理意义:基础矩阵 F 包含了更丰富的信息。它实际上是本质矩阵的“推广”:
- ( \mathbf{F} = \mathbf{K}_2^{-T} \mathbf{E} \mathbf{K}_1^{-1} )
- 其中 ( \mathbf{K}_1, \mathbf{K}_2 ) 分别是两个相机的内参矩阵。
- 因此,F 同时编码了两个相机的内参(K₁, K₂) 和它们之间的相对运动(R, t)。
-
你能从F中得到什么:
- 对极线约束:给定左图一点 p₁,其在右图上的对应点 p₂ 必然满足 ( \mathbf{F} \mathbf{p}_1 ) 所定义的直线上(即对极线)。这极大缩小了搜索范围,是立体匹配的基础。
- 立体校正:可以利用 F(进一步计算单应矩阵)将两幅图像重投影到共面行对准的平面上,使对极线变成水平扫描线,极大简化立体匹配。
- 如果已知内参K,则可以通过公式 ( \mathbf{E} = \mathbf{K}_2^T \mathbf{F} \mathbf{K}_1 ) 计算出本质矩阵 E,进而恢复运动。
简单理解:基础矩阵是“实用版”的关系,直接作用于我们看到的像素,在不知道相机内部细节时也能建立两幅图像的几何联系。
对比总结
| 特性 | 本质矩阵 | 基础矩阵 |
|---|---|---|
| 符号 | E | F |
| 使用条件 | 相机已标定(内参K已知) | 相机可未标定(内参未知) |
| 作用坐标 | 归一化坐标 (x = K⁻¹ * p) | 像素坐标 (p) |
| 包含信息 | 纯运动:仅旋转 R 和平移 t | 运动 + 内参:R, t, K₁, K₂ |
| 数学关系 | 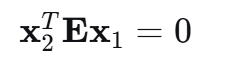 |
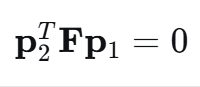 |
| 相互转换 |  |
|
| 主要用途 | 从图像恢复准确的相机运动(SLAM, SfM) | 建立图像间对应关系、立体校正、三维重建的第一步 |
| 自由度 | 5(因尺度等价性) | 7 |
一个生动的比喻
想象你要根据两张从不同角度拍摄的同一建筑物的照片,来确定你拍照时移动了多少。
- 基础矩阵 F:就像你拿到了两张带着不同边框和镜片畸变的照片。它告诉你:“第二张照片里,第一张这个窗户的位置,肯定在这条线上。” 它直接处理你手上拿着的“原片”。
- 本质矩阵 E:就像你用一个完美的标准工具,去掉了照片的边框,矫正了所有镜片畸变,只留下了纯粹的“视角信息”。它告诉你:“你的相机向右旋转了30度,并向前移动了5米。”
工作流程:
在实际的视觉系统中(如机器人、AR),我们通常:
- 先通过匹配特征点(如SIFT, ORB)估算出 基础矩阵 F。
- 如果相机已标定,则利用内参 K 从 F 计算出 本质矩阵 E。
- 最后从 E 中分解出相机运动 R 和 t,从而重建三维世界。


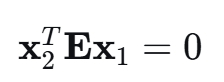
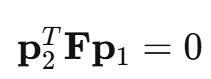

 浙公网安备 33010602011771号
浙公网安备 33010602011771号