相机坐标系下的3D点 ( X , Y , Z ) 转换到像素坐标系 ( u , v ) 需要使用相机的内参矩阵，怎么计算？

1. 相机内参矩阵

2. 坐标转换公式

``
// 假设已知相机内参
float fx = ...; // 焦距x (像素)
float fy = ...; // 焦距y (像素)
float cx = ...; // 主点x (像素)
float cy = ...; // 主点y (像素)

if (x < width && y < height) {
int idx = y * width + x;
float d = disparity[idx];
if (d == 0.0f) return;

const float q03 = Q[3];   // Q[0][3] = -cx
const float q13 = Q[7];   // Q[1][3] = -cy
const float q23 = Q[11];  // Q[2][3] = f
const float q32 = Q[14];  // Q[3][2] = -1/Tx
const float q33 = Q[15];  // Q[3][3] = (cx-cx')/Tx

float W = q32 * d + q33;
if (fabsf(W) > 1e-6f) {
    float Z = q23 / W;
    if (isnan(Z) || Z >= maxZ || Z <= minZ || Z == 0.0f) return;

    float X = (x + q03) * Z / q23;  // X = (x - cx) * Z / f
    float Y = (y + q13) * Z / q23;  // Y = (y - cy) * Z / f

    // 转换为像素坐标
    float u_pixel = fx * (X / Z) + cx;
    float v_pixel = fy * (Y / Z) + cy;

    point_cloud[idx] = {X, Y, Z};
    pixel_coords[idx] = {u_pixel, v_pixel};  // 存储像素坐标
}

}
``

3. 关键点说明

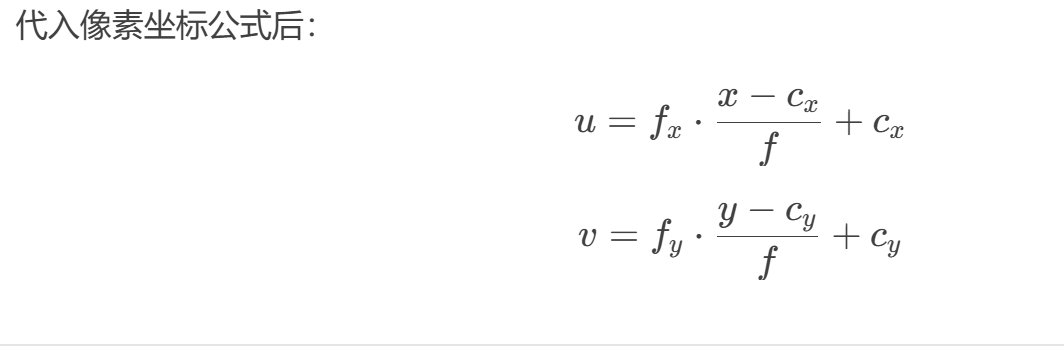
畸变校正：
如果相机镜头存在畸变，需先对 (u,v) 进行去畸变处理：
// 假设已计算去畸变映射表 (undistortMap)
cv::remap(raw_pixel_coords, undistorted_coords, undistortMap, cv::INTER_LINEAR);
坐标系一致性：
确保 Q矩阵中的 cx cy与内参矩阵 K 的定义一致。

世界坐标 (X,Y,Z) 到像素坐标 (u,v) 的转换为什么要1/Z？

(X,Y,Z) 到像素坐标系 (u,v) 的转换过程中，除以 Z（即深度值）是 透视投影（Perspective Projection） 的核心数学操作，其本质原因是 透视除法（Perspective Division）。

1. 透视投影的几何原理

相机成像遵循 小孔成像模型（Pinhole Camera Model），其核心特点是：近大远小：物体离相机越远，成像越小。
深度依赖性：投影后的坐标与深度 Z成反比。
数学上，3D点 (X,Y,Z) 到2D像素 (u,v) 的转换是一个非线性过程，需要通过齐次坐标和透视除法实现。

2. 齐次坐标与投影矩阵

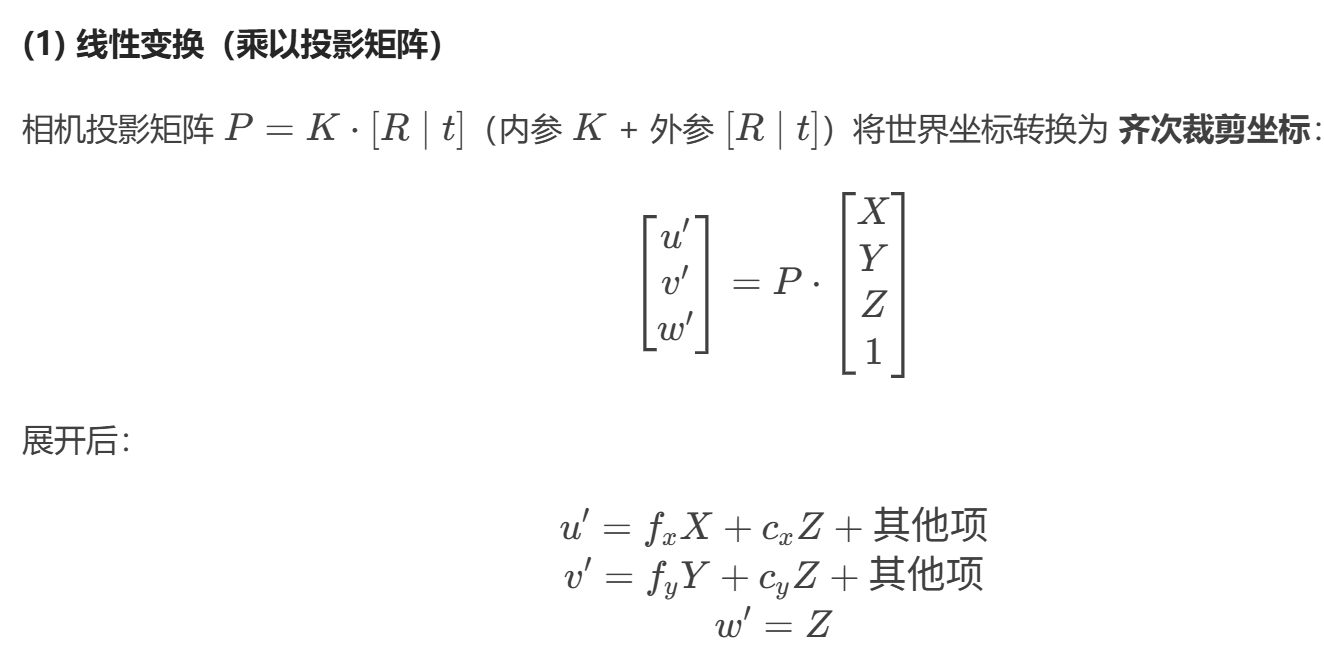
float X = (x + q03) * Z / q23; // 实际是 X = (x - c_x) * Z / f
float Y = (y + q13) * Z / q23; // Y = (y - c_y) * Z / f

// 转换为像素坐标时，需要除以 Z：
float u_pixel = fx * (X / Z) + cx; // = fx * (x - cx)/f + cx
float v_pixel = fy * (Y / Z) + cy; // = fy * (y - cy)/f + cy

注意：

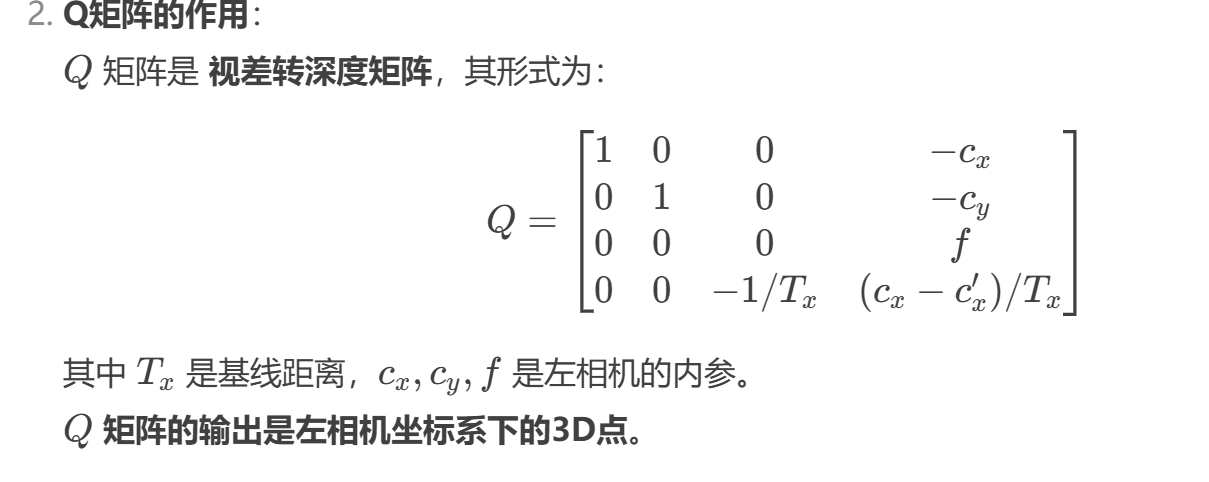
通过 Q矩阵 和 视差图 计算得到的 (X,Y,Z) 是 相机坐标系（Camera Coordinate System） 下的坐标，而非世界坐标系（World Coordinate System）

代码：
float X = (x + q03) * Z / q23; // 实际是 X = (x - cx) * Z / f
float Y = (y + q13) * Z / q23; // Y = (y - cy) * Z / f
X 和 Y 的计算基于 像素坐标 (x,y) 和 相机内参（隐含在 Q 矩阵中）
公式本质是 反向投影（Back-projection），将像素位置和深度转换为相机坐标系下的3D点。
直接使用 像素坐标
(x,y) 和 焦距 f（即 q23），这是相机坐标系的标准计算方式。
未涉及世界坐标系的旋转 R 或平移 t