标定的Q矩阵的参数意义

在结构光三维重建或立体视觉系统中，Q矩阵（重投影矩阵，Reprojection Matrix）是一个关键的 4×4 矩阵，用于将 二维图像坐标 + 视差（disparity） 转换为 三维世界坐标。它由相机标定（Stereo Rectification）过程生成，包含了双目系统的几何关系和相机参数。以下是 Q 矩阵的详细解析：

---

Q 矩阵的结构

通常形式为：

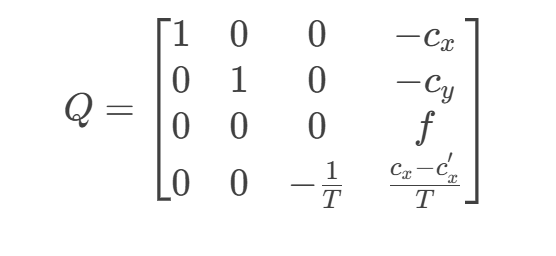
其中：

• ( (c_x, c_y) )：左相机主点（principal point）的像素坐标。
• ( c'_x )：右相机主点的 x 坐标（假设立体校正后仅 x 方向有视差）。
• ( f )：校正后相机的等效焦距（像素单位）。
• ( T )：双目系统的基线长度（baseline，即左右相机光心的水平距离，单位与焦距一致）。

---

Q 矩阵的参数意义

1. 前三行：坐标变换关系

• 第1行 [1, 0, 0, -c_x]
  将像素坐标的 ( x ) 方向平移至以主点 ( c_x ) 为原点。
• 第2行 [0, 1, 0, -c_y]
  将像素坐标的 ( y ) 方向平移至以主点 ( c_y ) 为原点。
• 第3行 [0, 0, 0, f]
  与视差 ( d ) 结合，计算深度 ( Z )（见下文公式）。

2. 第4行：深度计算核心

• [0, 0, -\frac{1}{T}, \frac{c_x - c'_x}{T}]
  这是深度计算的关键参数：
  • ( -\frac{1}{T} )：基线长度 T 的倒数，决定深度 Z的缩放比例。
  • ( \frac{c_x - c'_x}{T} )：校正后主点偏移的补偿项（立体校正后 c_x ≈ c'_x，此项通常接近 0）。

---

如何使用 Q 矩阵计算三维坐标？

给定左图像中的像素坐标 ( (x, y) ) 和视差 ( d )，三维坐标 ( (X, Y, Z) ) 的计算步骤如下：

---

Q 矩阵的实际意义

1. 视差转深度：
   ( Q ) 矩阵封装了 基线 ( T ) 和 焦距 ( f ) 的关系，直接关联视差与物理深度。
2. 坐标系统一：
   将左右相机的图像坐标统一转换到左相机坐标系下的三维坐标。
3. 校正后的简化计算：
   立体校正（Rectification）后，视差仅存在于水平方向，( Q ) 矩阵使得三维重建计算高效。

---

Q 矩阵的来源

• 通过 立体标定（Stereo Calibration） 和 立体校正（Stereo Rectification） 生成：
  1. 标定获取左右相机的内参（( K_{\text{left}}, K_{\text{right}} )）、外参（旋转 ( R )、平移 ( T )）。
  2. 校正过程计算左右图像的投影矩阵 ( P_{\text{left}}, P_{\text{right}} ) 和视差矩阵 ( Q )。

---

注意事项

1. 单位一致性：
   • ( f ) 和 ( T ) 需使用相同单位（通常为像素或毫米）。
2. 视差 ( d ) 的符号：
   • 根据库的实现不同，视差可能是 ( d = x_{\text{left}} - x_{\text{right}} ) 或其相反数，需与 ( Q ) 矩阵匹配。
3. OpenCV 中的 Q 矩阵：
   • 通过 stereoRectify() 函数计算，可直接用于 reprojectImageTo3D()。

---

示例（OpenCV 代码片段）

// 立体标定后获取 Q 矩阵
Mat Q;
stereoRectify(
    cameraMatrix1, distCoeffs1,  // 左相机内参和畸变
    cameraMatrix2, distCoeffs2,  // 右相机内参和畸变
    imageSize, R, T,             // 旋转和平移
    R1, R2, P1, P2, Q,          // 输出校正参数和 Q 矩阵
    CALIB_ZERO_DISPARITY
);

// 使用 Q 矩阵将视差图转换为三维点云
Mat disparity;  // 输入视差图（CV_16S 或 CV_32F）
Mat pointCloud; // 输出三维坐标（CV_32FC3）
reprojectImageTo3D(disparity, pointCloud, Q);

---

总结

• Q 矩阵 是连接 二维图像视差 与 三维世界坐标 的桥梁。
• 核心参数：焦距 ( f ) 和 基线 ( T )，决定深度计算的尺度。
• 应用场景：结构光三维重建、立体视觉、SLAM 等。