使用SVD或RANSAC求解变换矩阵
在点云匹配或三维配准中,SVD(奇异值分解)和RANSAC(随机抽样一致)是两种经典数学方法,用于求解最优的刚性变换矩阵(旋转 R 和平移 t),将源点云对齐到目标点云。以下是它们的核心原理和具体实现步骤:
1. SVD(奇异值分解)求解变换矩阵
适用场景
已知准确的对应点对(即已知源点云和目标点云中哪些点是匹配的),求解最优刚性变换。
数学原理
-
问题描述:
给定两组匹配的3D点集 ({p_i})(源点云)和 ({q_i})(目标点云),求旋转矩阵 (R) 和平移向量 (t),使得最小化误差:
![]()
-
步骤:
-
中心化:计算两组点集的质心,并将点坐标减去质心:
![]()
-
构建协方差矩阵:
![]()
-
SVD分解:对 (H) 进行奇异值分解:
![]()
-
求解旋转和平移:
![]()
-
代码实现(Python)
import numpy as np
def svd_transform(source, target):
# source, target: (N, 3) 的对应点集
mu_p = np.mean(source, axis=0)
mu_q = np.mean(target, axis=0)
H = (source - mu_p).T @ (target - mu_q) # 协方差矩阵
U, _, Vt = np.linalg.svd(H) # SVD分解
R = Vt.T @ U.T
# 处理反射情况
if np.linalg.det(R) < 0:
Vt[-1, :] *= -1
R = Vt.T @ U.T
t = mu_q - R @ mu_p
return R, t
优点与局限
- 优点:闭式解,计算高效,精度高(对应点准确时)。
- 局限:依赖准确的对应点对,对噪声和异常值敏感。
2. RANSAC(随机抽样一致)求解变换矩阵
适用场景
存在噪声或异常值(如错误匹配点对)时,鲁棒地估计变换矩阵。
数学原理
-
核心思想:
- 随机采样最小点集(如3对点)计算初始变换,统计内点(误差小于阈值的点)。
- 迭代选择内点最多的模型作为最优解。
-
步骤:
- 随机采样:从匹配点对中随机选取 (k) 个点(刚性变换最少需3对点)。
- 模型估计:用SVD计算当前采样点的变换 (R, t)。
- 内点检测:计算所有点对的变换误差
![]()
,保留误差小于阈值 (\epsilon) 的点。 - 迭代优化:重复 (N) 次,选择内点最多的模型,最终用所有内点重新拟合(SVD)。
代码实现(Python)
def ransac_transform(source, target, max_iters=1000, threshold=0.1):
best_R, best_t = None, None
best_inliers = []
for _ in range(max_iters):
# 1. 随机采样3对点
sample_idx = np.random.choice(len(source), 3, replace=False)
src_sample = source[sample_idx]
tgt_sample = target[sample_idx]
# 2. 用SVD计算变换
R, t = svd_transform(src_sample, tgt_sample)
# 3. 计算内点
transformed = (R @ source.T).T + t
errors = np.linalg.norm(transformed - target, axis=1)
inliers = np.where(errors < threshold)[0]
# 4. 更新最优模型
if len(inliers) > len(best_inliers):
best_inliers = inliers
best_R, best_t = R, t
# 5. 用所有内点重新拟合
if len(best_inliers) >= 3:
best_R, best_t = svd_transform(source[best_inliers], target[best_inliers])
return best_R, best_t
参数选择
-
阈值 (\epsilon):根据点云噪声水平设定(通常为点云平均间距的2-3倍)。
-
迭代次数 (N):
![]()
其中 (p) 为置信度(如0.99),(e) 为异常值比例,(k) 为最小采样数。
优点与局限
- 优点:对异常值鲁棒,适合部分重叠或噪声大的点云。
- 局限:计算耗时,需调参(阈值、迭代次数)。
3. SVD与RANSAC的对比
| 方法 | 输入要求 | 抗噪声能力 | 计算效率 | 适用场景 |
|---|---|---|---|---|
| SVD | 精确的对应点对 | 弱 | 高 | 已知准确匹配(如ICP的最后一步) |
| RANSAC | 可能含异常值的点对 | 强 | 低(依赖迭代) | 初始粗配准、存在错误匹配时 |
4. 实际应用中的结合
- 粗配准 + 精配准:
- 先用RANSAC剔除异常值,得到初始变换。
- 再用SVD对所有内点优化,提升精度。
- 深度学习结合:
- 用神经网络(如DCP)预测点对对应关系,再用SVD/RANSAC求解变换。
总结
- SVD:通过闭式解求最优变换,需输入准确对应点,适合精配准。
- RANSAC:通过迭代采样鲁棒估计,适合存在噪声或异常值的场景。
- 联合使用:RANSAC初筛 + SVD精修是经典流程(如ICP算法中的变种)。



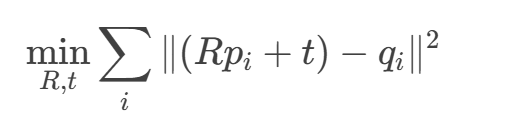

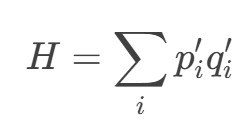
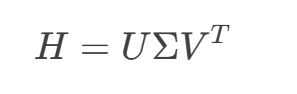
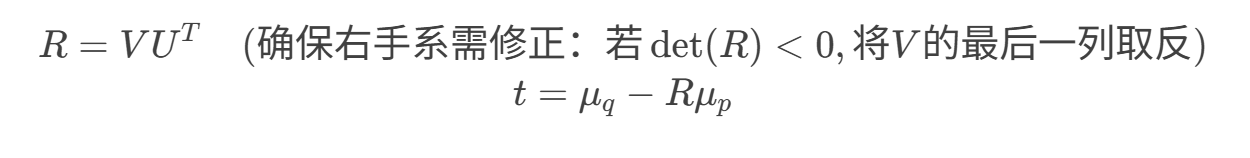
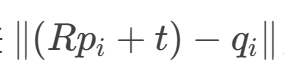
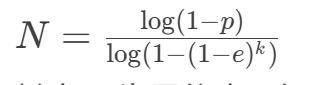

 浙公网安备 33010602011771号
浙公网安备 33010602011771号