LFM雷达信号仿真

本文利用matlab软件对LFM信号进行仿真实验

FMCW信号生成

概要

常见的正余弦信号有固定的周期，即频率是固定的。而FMCW信号是一种频率线性变化的信号，这使得该信号不仅能够完美保留回波信号的相位信息，进行测距测速测角。

实验仿真

T=10e-6; %脉宽
B=30e6; %带宽
K=B/T; %调频斜率
Fs=2*B;Ts=1/Fs; %采样频率和采样间隔
N=T/Ts; %采样点
t=linspace(-T/2,T/2,N); %时间轴

% 图一：生成包含实部虚部的LFM信号
St=exp(j*pi*K*t.^2);
plot(t*1e6,real(St));

% 图二：对信号做FFT，将信号从时域转到频域
plot(freq*1e-6,fftshift(abs(fft(St))));

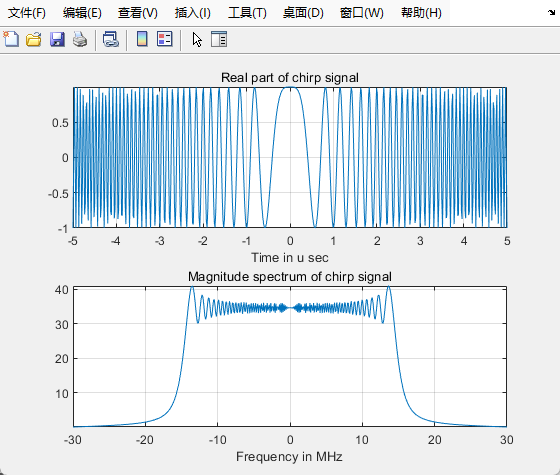
结论

• fftshift：对时域信号做fft后转为频域信号，零频率在开头，负频率轴在中心点右边，做fftshift使得零频位于中心。[0, 1, 2, ..., N/2, ..., -N/2+1, ..., -2, -1] -> [-N/2, ..., -1, 0, 1, ..., N/2-1]
• abs：使得复数信号转为正实数，显示为幅度（模值），对应信号的强度。

对LFM信号做脉冲压缩

概要

LFM信号如上一节所示，FFT后在零频左右两侧出现一条平缓的脉冲，能量被分散在很长的脉宽T上，无法对其研究。脉冲压缩技术使得信号能量聚集，生成一个一个的“瓣”，脉宽被压缩T -> 1/B，带宽增加，距离分辨率增加。

实验仿真

St=exp(j*pi*K*t.^2); %chirp信号
Ht=exp(-j*pi*K*t.^2); %匹配滤波器
Sot=conv(St,Ht); %匹配滤波后的信号

% 图一：匹配滤波后的信号和sinc函数的散点图，两者在(-T,T)内可以近似相同
t1=linspace(-T,T,L);
Z=abs(Sot);Z=Z/max(Z);
Z=20*log10(Z+1e-6);
Z1=abs(sinc(B.*t1));
Z1=20*log10(Z1+1e-6);
t1=t1*B;
plot(t1,Z,t1,Z1,'r.');

% 图二：坐标轴设置为3T

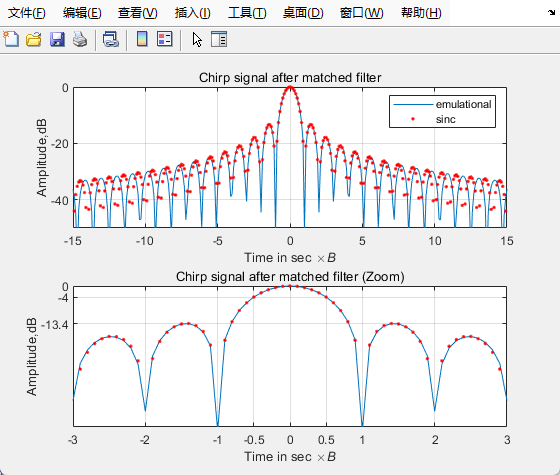
结论

• 匹配滤波后信号呈现出"旁瓣-主瓣-旁瓣"的形式
• 根据sinc函数方程：\(S_o(t)=TSa(\pi KTt)rect(\frac{t}{2T}=TSa(\pi Bt)rect(\frac{t}{2T})\)
  当\({\pi}Bt=\pm\pi\)，\(t=\pm\frac{1}{B}\)为函数第一零点坐标；当\({\pi}Bt=\pm\frac{\pi}{2}\)，\(t=\pm\frac{1}{2B}\)，此时脉宽为\(\tau=\frac{1}{2B}\times2=\frac{1}{B}\)。相比于原脉宽T缩小了300倍，能量得到聚集