梯度下降

梯度下降(Gradient Descent)是机器学习、深度学习中常用的优化方法，能够使得模型参数达到局部或整体最优值

本质

• 从一个初始点出发，沿着损失函数的负梯度方向不断更新参数，直到达到一个局部最小值或者全局最小值

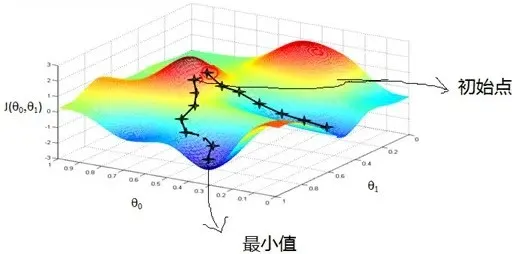
过程

1. 初始化参数：选择一个初始的参数值

2. 计算梯度：计算损失函数在当前参数值下的梯度

3. 更新参数：沿着梯度的反方向更新参数，通常使用一个学习率（Learning Rate）来控制更新的步长

4. 重复迭代：重复步骤2和3，直到满足停止条件（如达到最大迭代次数、损失函数值小于一个阈值等）

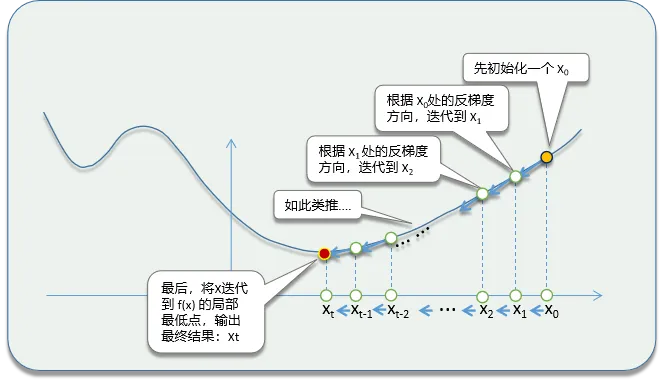
原理

• 在梯度下降中，利用方向导数的最小值（即梯度的反方向）来更新参数，从而逼近函数的最小值

方向导数：函数沿某方向的变化率
梯度：函数在某一点的最大变化率和该变化发生的方向

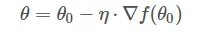
公式推导：
简单的梯度下降算法，你真的懂了吗？
梯度下降算法详解（从下山比喻、数学推导到代码实现）

常用算法

• 批量梯度下降（BGD）：在每次迭代中，批量梯度下降使用整个数据集来计算损失函数的梯度，并根据这个梯度来更新模型的所有参数（方便用，效率低）

• 随机梯度下降（SGD）：与批量梯度下降不同，随机梯度下降在每次迭代中仅随机选择一个样本来计算损失函数的梯度，并根据这个梯度来更新模型的一个或多个参数（用起来麻烦；效率高）

参考资料：神经网络算法 - 一文搞懂Gradient Descent（梯度下降）

个人学习用，侵权删