前向传播(FP)和反向传播算法(BP)

前向传播和反向传播是神经网络训练过程中两个重要的环节，分别决定了预测的最终结果以及权重参数的调整

案例引入

假设有神经网络如下图所示：

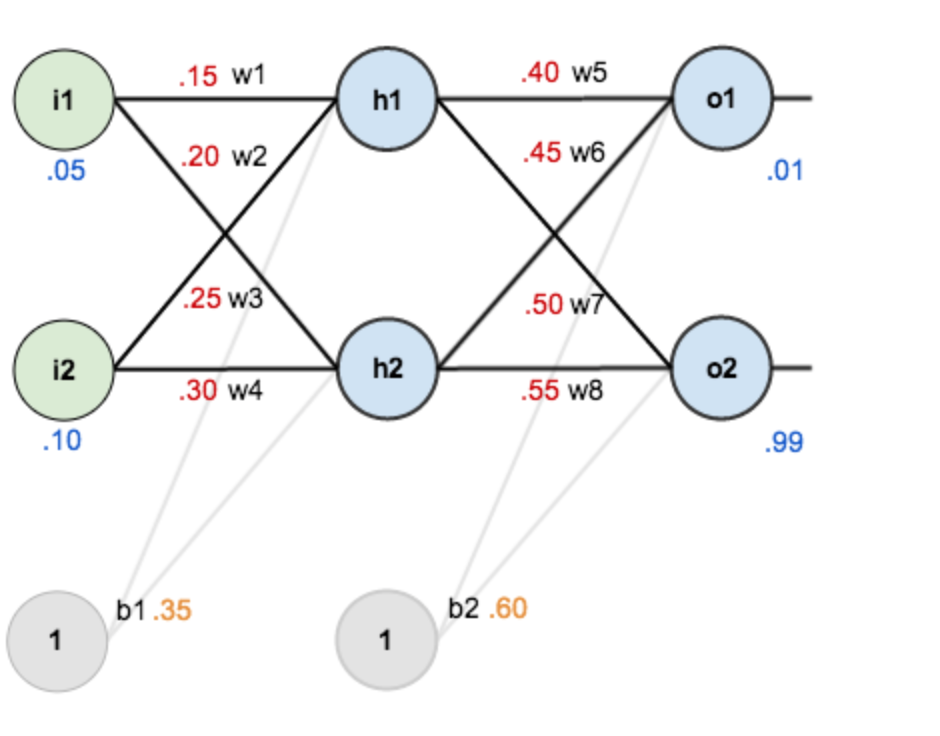
• 第一层是输入层，包含两个神经元i1，i2和截距项b1
• 第二层是隐含层，包含两个神经元h1,h2和截距项b2
• 第三层是输出o1,o2，每条线上标的wi是层与层之间连接的权重，激活函数我们默认为sigmoid函数。

其中，

• 输入数据 i1=0.05，i2=0.10
• 输出数据 o1=0.01,o2=0.99
• 初始权重 w1=0.15,w2=0.20,w3=0.25,w4=0.30;w5=0.40,w6=0.45,w7=0.50,w8=0.55

问：如何调整参数wi，使得输入数据经过神经网络得到的输出尽可能和真实输出值接近？

答：
1、输入数据，使用当前 wi 参数值计算得到一轮输出值，与真实值对比，并计算误差；
2、利用求导的链式法则，从输出到输入分别计算各 wi 参数的偏导数，并利用误差公式更新各 wi 参数值
3、重复上述操作，直至输出值与真实值接近

简单来说，前向传播就是往机器里面输入数据，跑出来结果；反向传播就是修改机器里的零件，使得前向传播输出的值更接近真实值。下面通过三个小标题的内容依次讲解

1. 前向传播

1. 输入层---->隐含层：

• 计算神经元h1的输入加权和
  

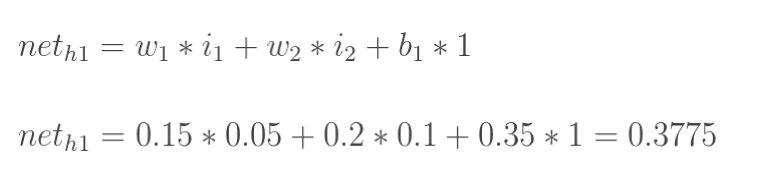
• 神经元 h1 的输出 o1:(此处用到激活函数为 Sigmoid 函数)
  

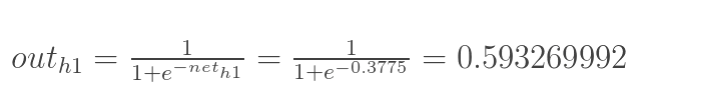
• 同理，可计算出神经元 h2 的输出 o2
  

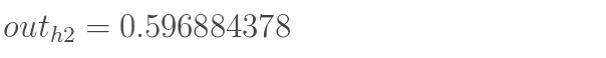
2. 隐含层---->输出层：

• 计算 o1 和 o2 的值
  
  

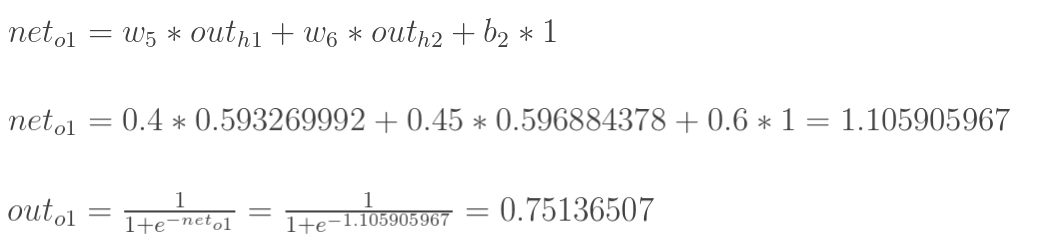
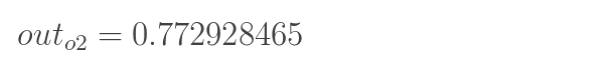
• 输出值为 [0.75136079 , 0.772928465]，与实际值 [0.01 , 0.99] 仍有差距

2. 反向传播

• 计算总误差

• 这里我们选用均方误差（MSE）
  
  
  
  

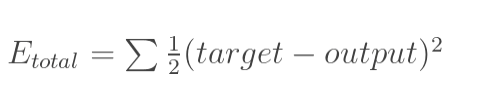
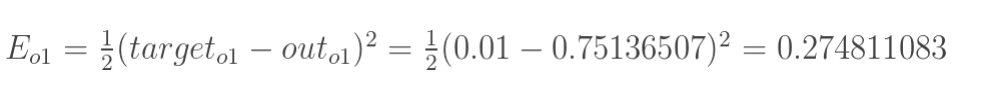
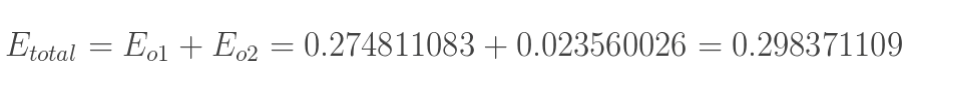
1. 输出层---->隐含层：

• 以权重参数 w5 为例，求 w5 对整体产生的影响，可以用整体误差对 w5 求偏导（链式法则）
  

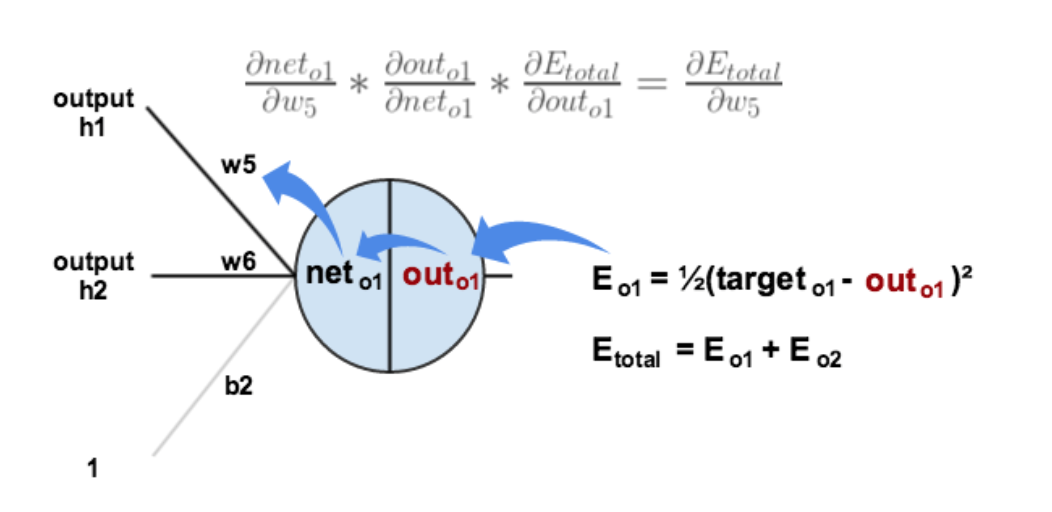
• 下面来分别计算这三个偏导数

• Etotal 对 outo1 的偏导数
  

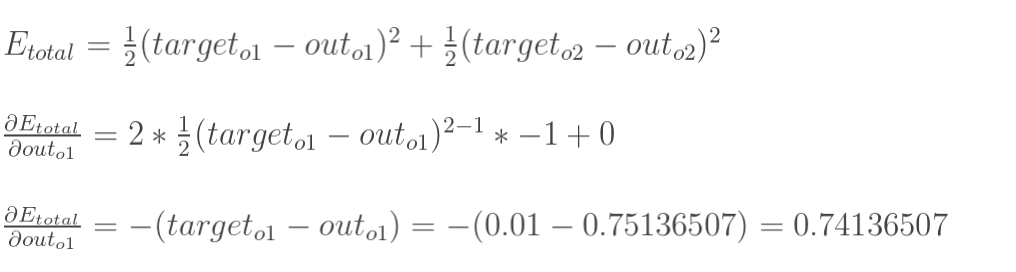
• outo1 对 neto1 的偏导数
  

• neto1 对 w5 的偏导数
  

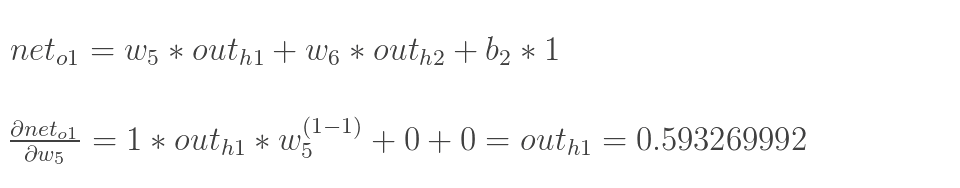
• 将三者相乘
  

• 将上面三个公式合并：
  

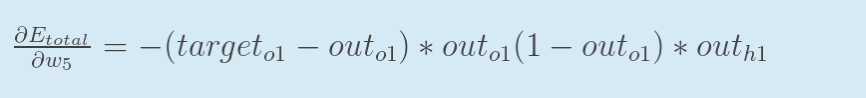
• 为表达方便，用 \(\delta\)(o1) 表示输出层的误差
  

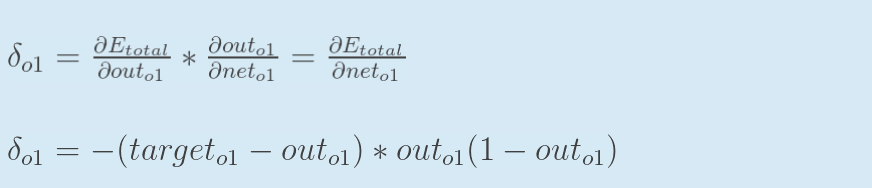
• 整体误差对 w5 的偏导（输出层误差记为负）
  

• 更新 w5 的值
  
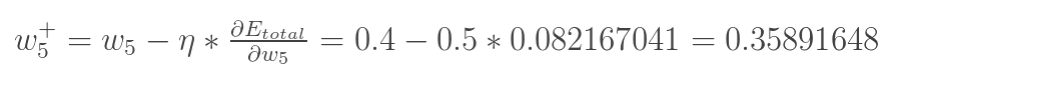
  （其中，\(\eta\) 是学习速率，这里我们取0.5）

• 同理，更新 w6 w7 w8
  

2. 隐含层---->输入层：

• 与 w5 参数的计算略有不同，w1 参数除了要接受 E(o1) 传来的的误差，还要接受 E(o2) 传来的的误差
  

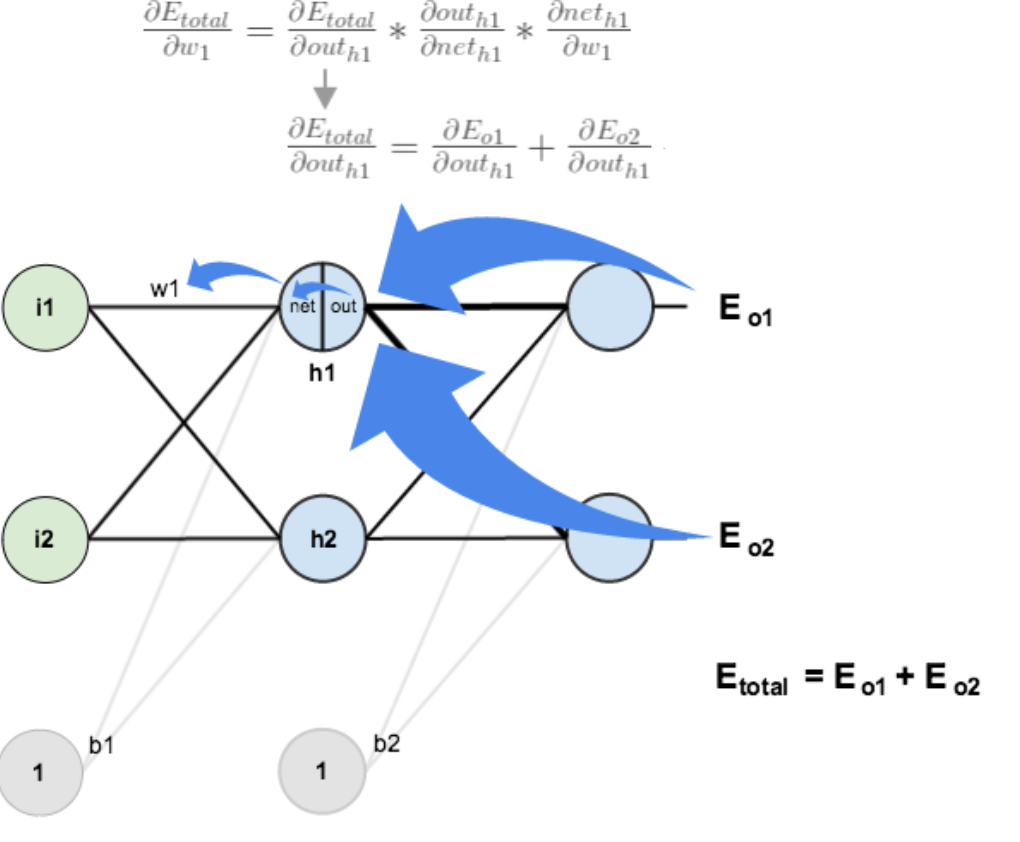
• E(total) 对 out(h1) 的偏导数
  

• E(o1) 对 out(h1) 的偏导数
  
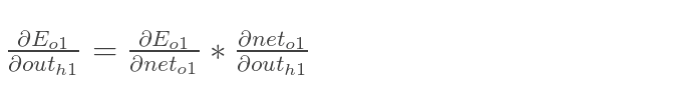
  // TODO 此处是否还需计算 E(o1) 对 out(o1) 的偏导？
  
  
  

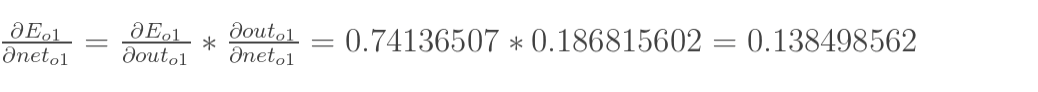
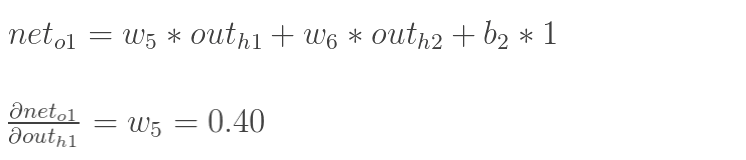
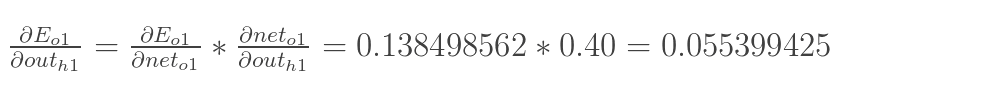
• 同理，E(o2) 对 out(h1) 的偏导数
  

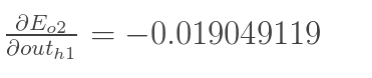
• 两者相加可得
  

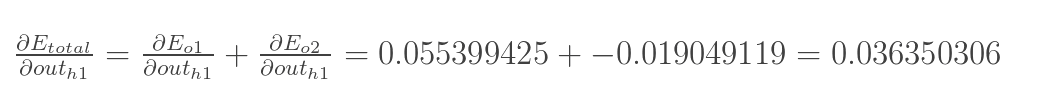
• out(h1) 对 net(h1) 的偏导
  

• net(h1) 对 w1 的偏导
  

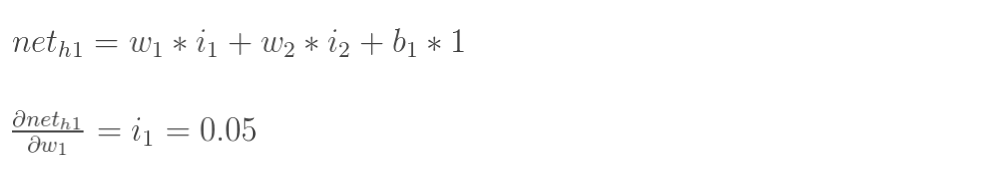
• 三者相加
  

• 为了简化，用 \(\delta\)(h1) 表示隐含层单元 h1 的误差
  

• 更新 w1 权值
  

• 更新 w2 w3 w4 的权值
  

3. 重复

• 重复上述前向传播、反向传播操作，直到输出值与真实值的误差到达可接受范围
• 需要代码学习的同学可参考这篇文章“反向传播算法”过程及公式推导（超直观好懂的Backpropagation）

参考资料：
一文弄懂神经网络中的反向传播法——BackPropagation
“反向传播算法”过程及公式推导（超直观好懂的Backpropagation）

个人学习用，侵权删