菜鸟根据周志华老师pdf所写，盗了点图望谅解

错了请联系我更正

泛化误差  vs 经验误差

泛化误差：在‘“未来”样本上的误差

经验误差：在训练集上的误差 ps：个人觉得应该是在训练的过程中所带来的误差

误差是不是越小越好？

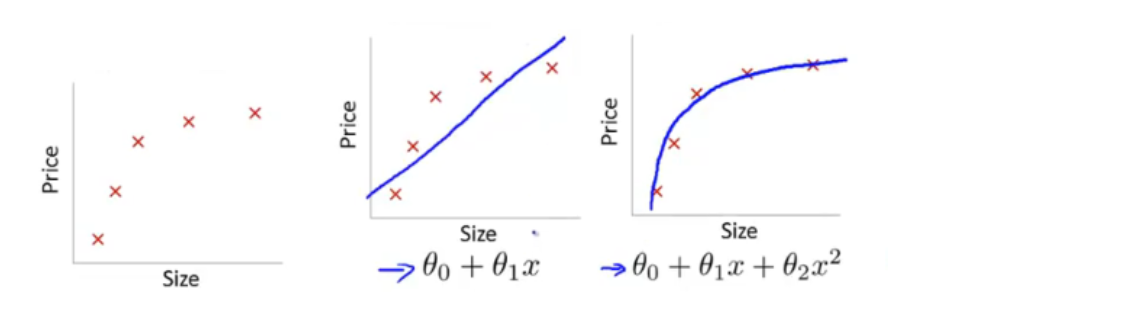
过拟合：如图3  ps：模型泛化能力太差，只能解决当前验证集 解决办法：增大数据的训练量， 采用正则化方法

欠拟合：模型没有很好地捕捉到数据特征，不能够很好地拟合数据  解决办法：增加特征量，减少正则化参数 正则化的出现是防止过拟合的 如图2

 

模型选择（评估方法，性能度量，比较检验）

评估方法：留出法，折交叉验证法，自助法

留出法：直接把集合 分为训练集和测试集，两个互斥 ，注意：两个集合需保持数据分布一致性。多次重复划分，测试集不能太大。也不能太小（0.2~0.3） ps：假如 某验证集正好取到一种特殊类型数据，就会带了额外误差，当数据明显的分为有限类时， 采取分层抽样选择测试数据，

折交叉验证法：交叉验证用于防止模型过于复杂而引起的过拟合.有时亦称循环估计， 是一种统计学上将数据样本切割成较小子集的实用方法。我们先在一个子集上做分析其他子集用来验证。一开始的称之为训练集，而其他的子集称之为验证集 要求：训练集的比例足够多，一般大于一半，训练集和测试集要均匀抽样 k—交叉验证 k个子集 每个子集做一次测试集，其余作为训练集 重复k次，每次选择一个子集作为测试集，并将k次平均交叉验证识别正确率作为结果 优点：在每次循环中 所有的样本都用来训练model，因此最接近母体样本的分布，在训练过程中排出了随机因素的影响

自助法：

 

性能度量：是衡量模型泛化能力的评价标准，反映了任务需求 模型的好坏 不仅取决于算法与数据，还取决于任务需求

回归任务中常用均方误差 理解：预测值减去实际值的平方的和除以总数， 代价函数 

错误率 +精度（精确率）  = 1  图一错误率 图二精确率 ps：个人觉得 应该是一个预测函数，和一个真实函数 如果两个值相等 则属于图二，不等则属于图一

 

 

 

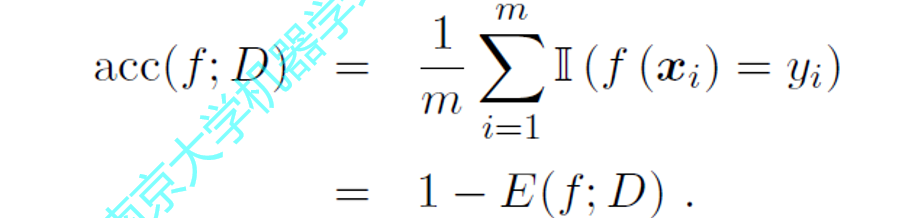
比较检验

在某种度量下得到的评估结果，能否作为评价优劣的依据？ NO

测试性能 ！= 泛化性能

测试性能随着测试集的改变而改变

算法具有一定随机性

 

机器学习之“误差从哪儿来”

 

泛化性能是由学习算法的能力，数据的充分性以及学习任务本身的难度共同决定

 

方差：很多人应该都还记得在统计学中, 一个随机变量的方差描述的是它的‘’离散程度‘’, 也就是该随机变量在其期望值附近的 波动程度 . 取自维基百科一般化的方差定义:

偏差：这里的偏指的是 偏离 , 那么它偏离了什么到导致了误差? 潜意识上, 当谈到这个词时, 我们可能会认为它是偏离了某个潜在的 “标准”, 而这里这个 “标准” 也就是真实情况 (ground truth). 在分类任务中, 这个 “标准” 就是真实标签 (label).

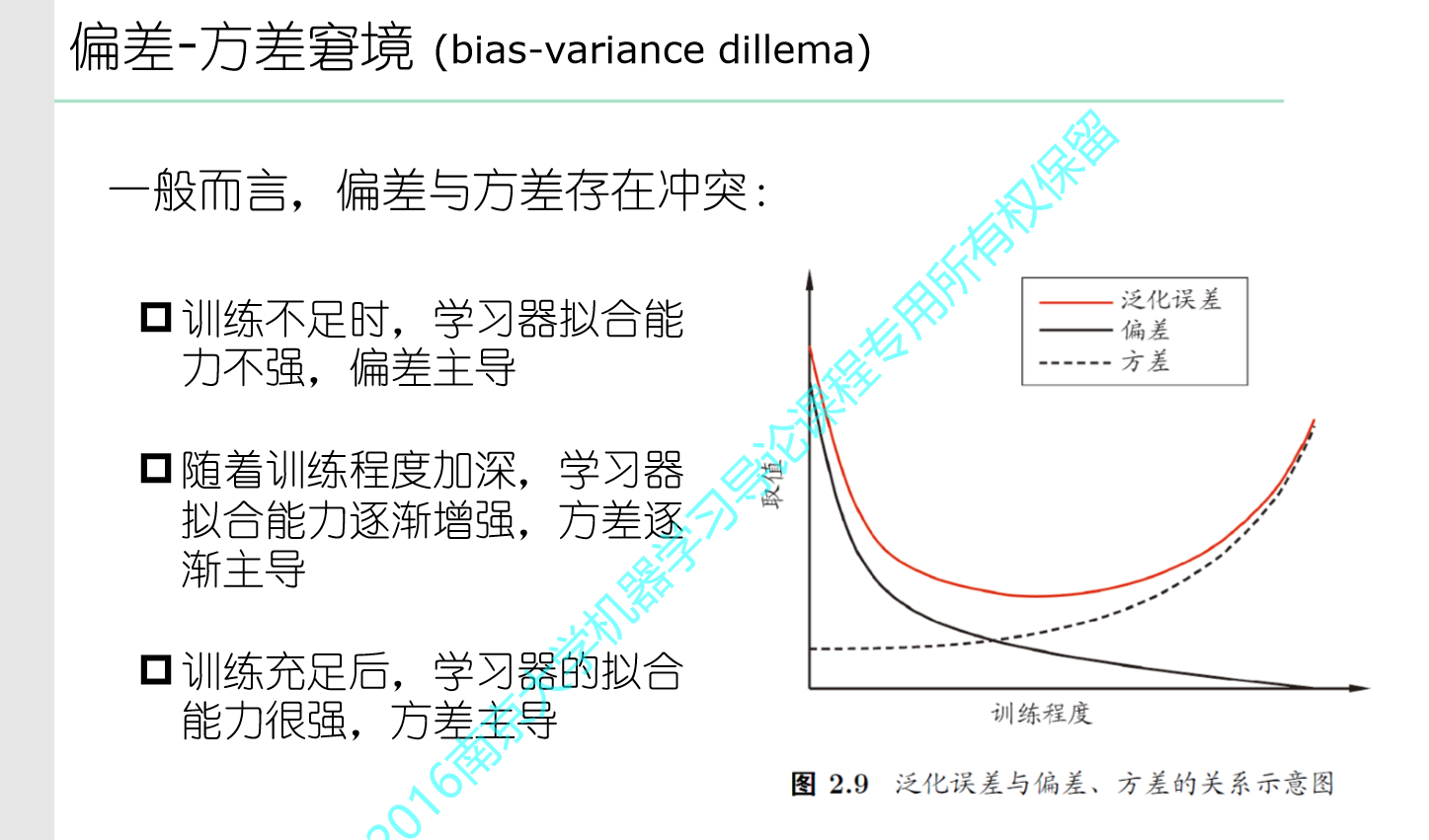
高方差 低偏差 导致过拟合，低方差 高偏差 导致欠拟合 ps：

降低方差：增大数据，减少特征量

降低偏差：增大特征量，减少数据

一般采取判断某函数是高方差还是高偏差，简单的判断是看训练误差与测试误差的差距，差距大说明是高方差的，差距小说明是高偏差的。