SciTech-Mathmatics-坐标基 + 基变换 + 一维列向量坐标的变换: 左乘变换矩阵 而 一维行向量的坐标系基元的变换 是 右乘变换矩阵 + PCA(Principal Components Analysis)主成分分析
SciTech-Math-PCA(Principal Components Analysis)主成分分析: 坐标基 + 基变换 + 一维列向量坐标的变换: 左乘变换矩阵 而 一维行向量的坐标系基元的变换 是 右乘变换矩阵
https://zhuanlan.zhihu.com/p/661060377
总结:
- 坐标与坐标系(基向量组=变换矩阵)是成对出现。同一点在不同坐标系的坐标的变换,要有统一的“世界坐标系”
- 坐标(一维列向量)变换: 左乘 变换矩阵;只是改变“视角”,都是同一点在不同坐标系去描述
- 基元(一维行向量)变换: 右乘 变换矩阵;基元(坐标系)发生改变, 是将一坐标系转为新坐标系
类比:
- 长度的数值与单位是成对出现,
- 同一物体的长度L,需要有统一的metrics公米制才可以进行换算:
Feet(US), Inch(UK), Miles, nautical(sea) Miles, Yards, Light-Year; - 长度变换:物体的长度始终是 1m, 在不同制的尺测量值有:
1m = 3.2808333Feet(US) = 39.370079Inch(UK)
= 0.00062Miles = 0.00054Naut.Miles = 1.094Yards. - 测度制变换:Inch制测度尺 变换到 Metrics制测度尺。
测度高维空间的点的位置需要:
- 建立坐标系:首先建立坐标系,选择哪些维度,每个维度的参考点;
- 其次将点位置投射到此坐标系的每一维度,得到对应维度上的测度;
- 正式表示:表示坐标系的坐标基矩阵乘上点坐标(该坐标系上的)。
数学表示: 坐标系的坐标基矩阵乘上点坐标(该坐标系上的):
⚠️注意:以下表达式的小写字母:头上有 “\(\large \rightarrow\)”的是\(\large vector\);没有的是\(\large Scalar\);
在描述空间的某个点时可以将其描述为:![]()
坐标系的坐标基矩阵乘上点坐标(该坐标系上的).
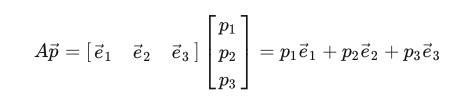
- 此空间坐标系A的坐标基矩阵(本文坐标系的基向量都为标准正交基):
![]()
- 此空间的p点在坐标系A的点坐标:
![]()
也可以将其看成世界坐标系的点坐标(世界坐标系以单位阵为坐标系坐标基矩阵):
引入世界坐标系的必要性: 是因为它将在后续的 坐标变换 及 坐标系变换,充当转换站的Role。
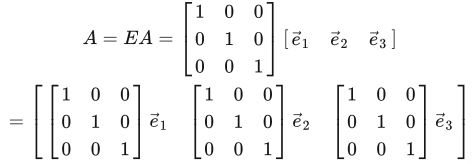
上式的单位阵为:

坐标变换与坐标系变换
实际应用经常会遇到多个坐标系以及其对应的坐标的情况,比如:
坐标系A及其对应的坐标![]() 和 坐标系B及其坐标
和 坐标系B及其坐标![]() 。
。
我们假设它们之间存在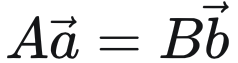 , 也就是空间的同一个点用不同坐标系下的坐标来描述。因此有:
, 也就是空间的同一个点用不同坐标系下的坐标来描述。因此有: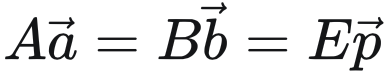
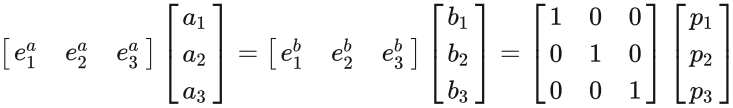
上式的基向量![]() 代表它是坐标系A的基向量,同时实际上也等于世界坐标系乘以世界坐标的形式即
代表它是坐标系A的基向量,同时实际上也等于世界坐标系乘以世界坐标的形式即![]() 。
。
坐标系A实际上是对世界坐标系进行A对应的初等列变换后得到的。
坐标系A的每个列向量,事实上都是对世界坐标系的三个基向量进行线性加和后得到的。
-
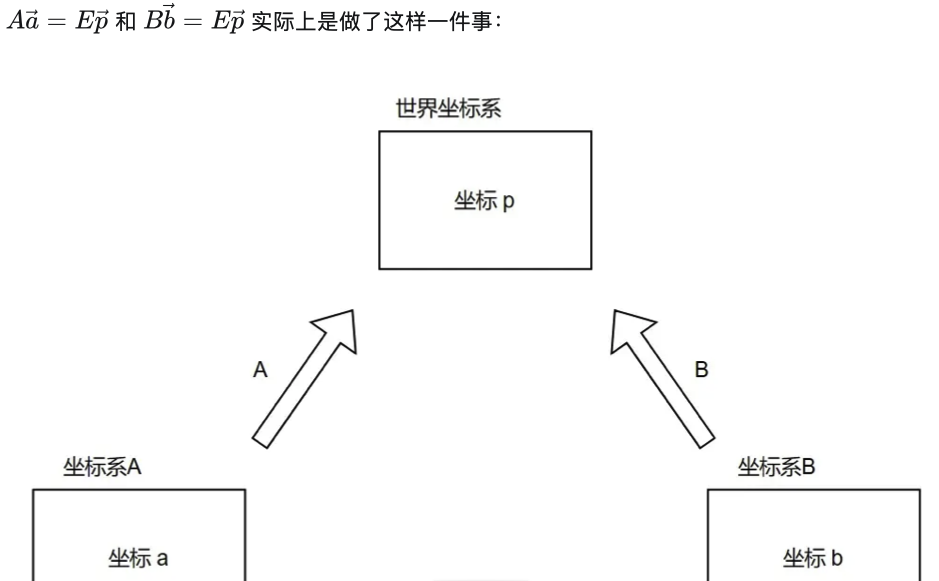
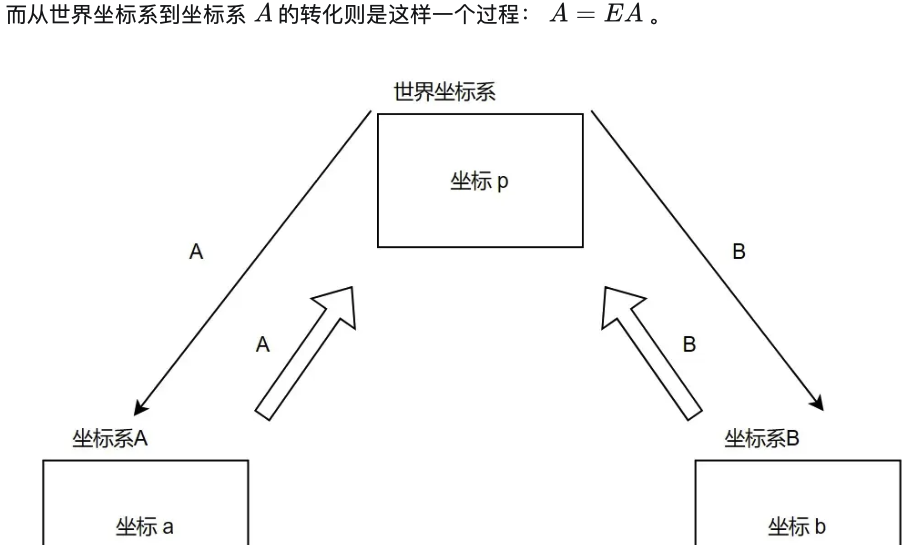
将 坐标系A上的坐标a 与 坐标系B上的坐标b 转化为 世界坐标系上的坐标p :
![]()
-
世界坐标系到坐标系A或B的转化过程则是:
![]()
坐标变换
-
坐标变换定义:把一个向量(或一个点)从一个高维(或3D)坐标系,转换到另一个高维(或3D)坐标系去。
通过将旧坐标A0, 左乘一个变换矩阵 T, 就可以实现。 -
注意:坐标变换 是 左乘(变换矩阵T 是 乘在左边)的。 变换: T * A0 = A1, 此处 旧坐标A0,新坐标A1 都是一维列向量;
-
坐标变换矩阵 T 乘在左边 是因为坐标多是用一维列向量表示,因此过渡矩阵A只能被乘到左边。
-
坐标系基元(基元为一维行向量)的变换 是 右乘 变换矩阵,举个栗子就可以分清:
已知坐标系基元为 (i, j, k),基元为一维行向量表示, 因而基元的变换只能是右乘.
举个栗子:A1.shape(1,3)= A0.shape(1, 3) * T.shape(3,3)。


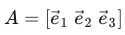
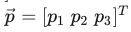

 浙公网安备 33010602011771号
浙公网安备 33010602011771号