SciTech-Math-Space&Coordination: 空间、视角(场景)及其坐标、变换(空间和坐标): Euclidean Space And Non-Euclidean Space + Inner Product Space + Fourier Series + Hilbert Space
SciTech-Math-Space&Coordination: 空间、视角(场景)及其坐标: Euclidean Space(欧式空间) And Non-Euclidean Space(非欧空间)
Space (空间) 的 总结
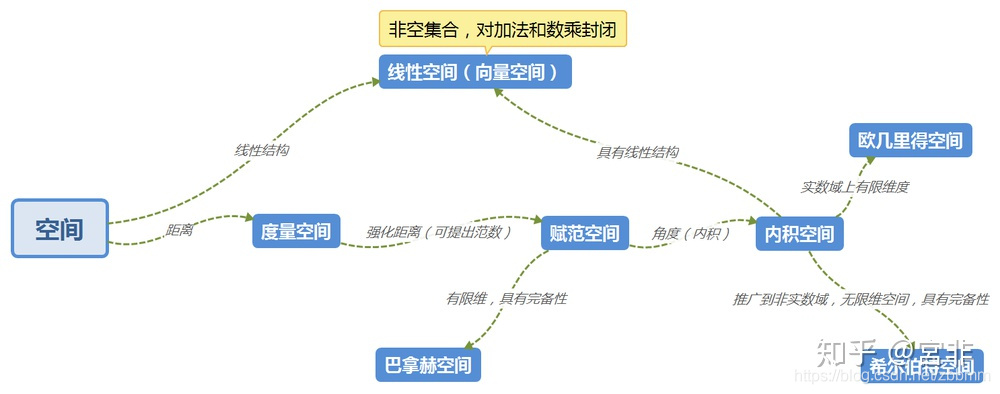
欧几里得空间(来源: 数学天地)
\(欧几里得 n-空间\),有时称为 \(笛卡尔空间\) 或简称 \(n-空间\),是所有 n元组 实数,(x_1, x_2, ..., x_n) 的空间。
这样的 \(n-元组\) 有时称为点,尽管可以使用其他术语(见下文)。
\(n-空间\) 的全体通常表示为$ R^n$,尽管较旧的文献使用符号 \(E^n\)(或者实际上,是非双线体变体 \(E^n\);O'Neill 1966,第 3 页)。
$R^n $ 是向量空间,具有 \(Lebesgue 覆盖维数 n\)。 因此,\(R^n\) 的元素有时称为 $ n-向量$。
不同空间 的 "距离" 定义和转换
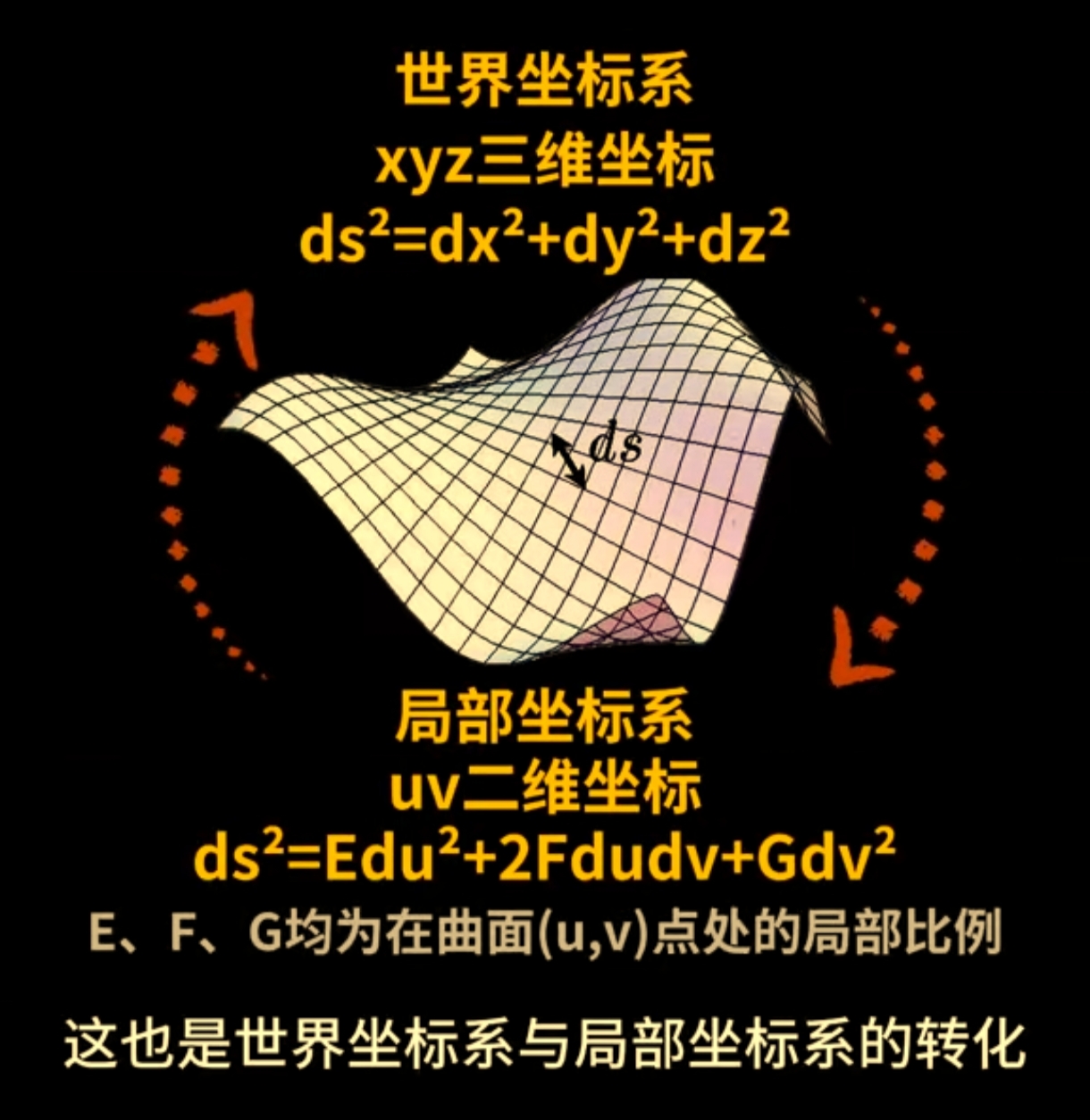
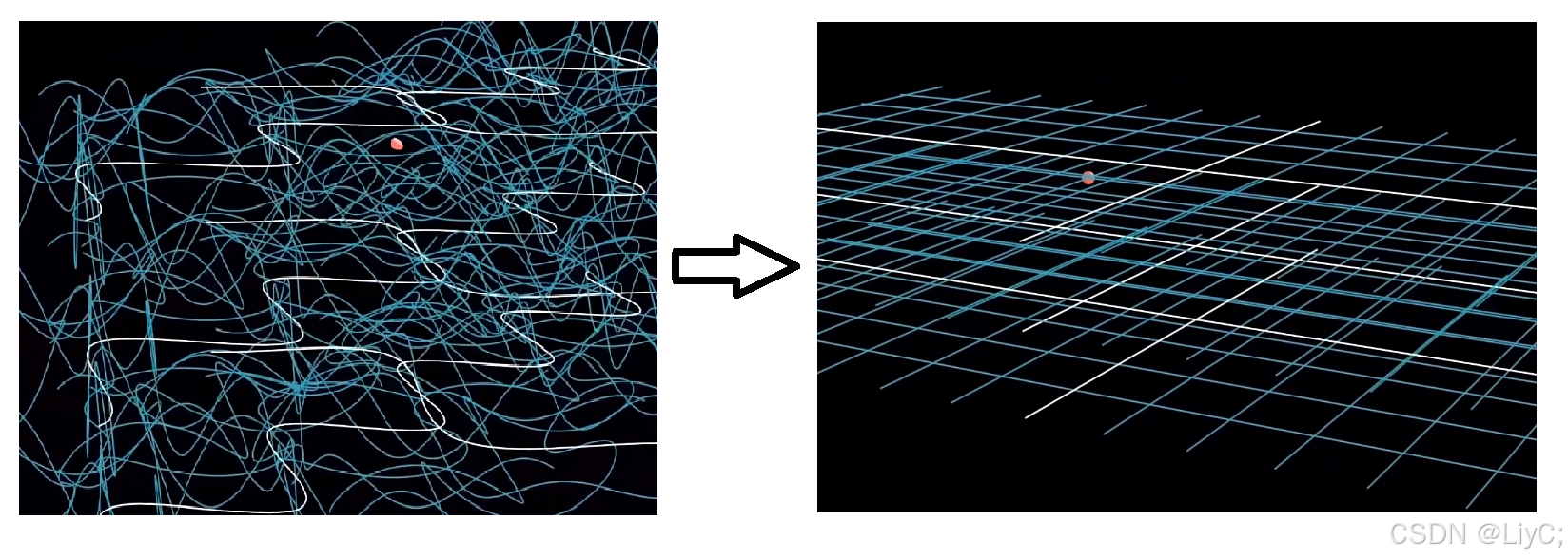
| 对比坐标系: 世界 VS 局部 | 不同坐标系 的 线元计算 与 转换 |
|---|---|
 |
 |
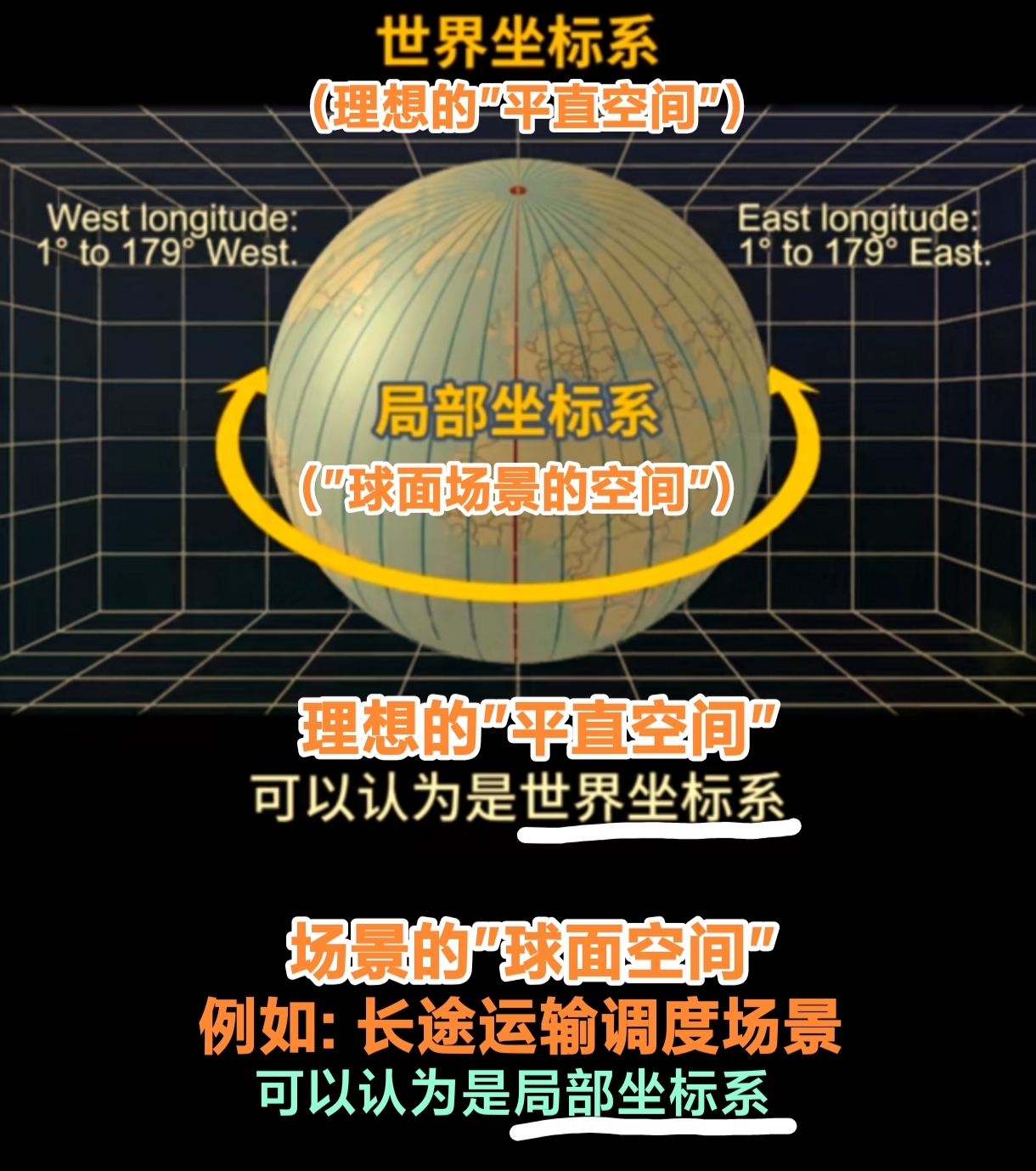
| 世界(平直) 坐标系 |  |
 |
 |
 |
|---|---|---|---|---|
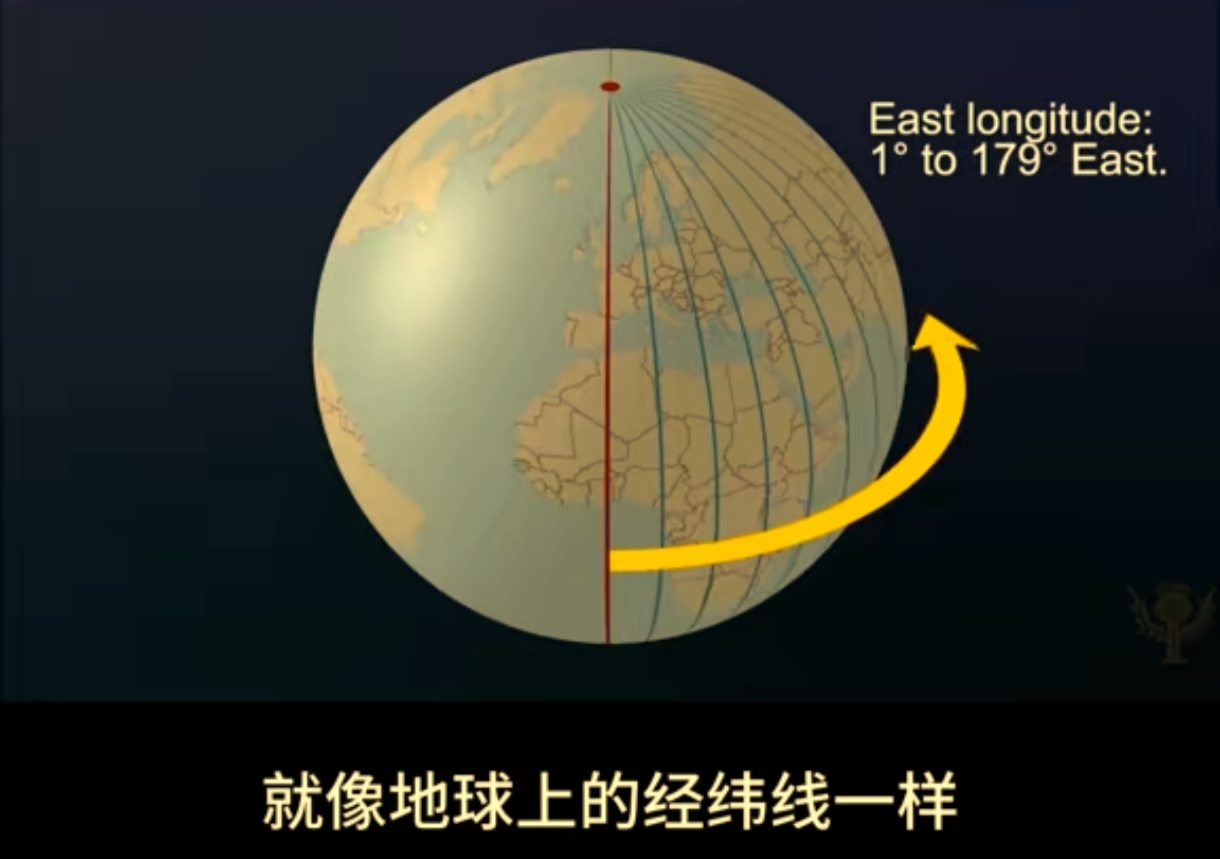
| 局部(曲面) 坐标系 |  |
 |
 |
 |
Euclidean Space(欧式空间) And Non-Euclidean Space(非欧空间)
世界坐标系(Euclidean Space):
Euclidean Space(欧式空间)的本质性,是其平面性.
一句话总结:Euclidean Space就是在对现实空间的规则抽象和推广(从n<=3 推广到 有限n维空间)。
- 欧几里得几何 就是中学学的 平面几何、立体几何,
中学学的几何空间, 一般是低维空间, 如 2维,3维. 所以,我们讨论余弦值、点间的距离、内积都是在低维空间总结的. - 欧几里得几何中,平行线任何位置的间距相等。
- 如果, 将这些低维空间所总结的规律推广到有限的n维空间,
那么, 这些符合定义的空间, 则统称为 欧式空间(Euclidean Space, 欧几里得空间)。 - Euclidean Space主要是定义: 内积、距离、角(没错,就是初中的那些定义],
理解了这些再去理解数学定义就很明确。

- 空间坐标系及其坐标的相互转换:
https://www.cnblogs.com/abaelhe/p/17917804.html
Euclidean Space(欧几里得空间)
欧几里得几何就是中学学的平面几何、立体几何,
在欧几里得几何,两平行线任何位置的间距相等。
- 中学学的几何空间一般是2维,3维; 所以,我们讨论 余弦值、点间的距离、内积 都是在低维空间总结的.
- Euclidean Space :将这些低维空间所总结的规律, 推广到有限的n维空间,那这些符合定义的空间, 则统称为欧式空间。
- Euclidean Space
主要定义了内积、距离、角。
傅里叶级数
在说明Hilbert Space之前,我们先了解什么是Fourier Series。
-
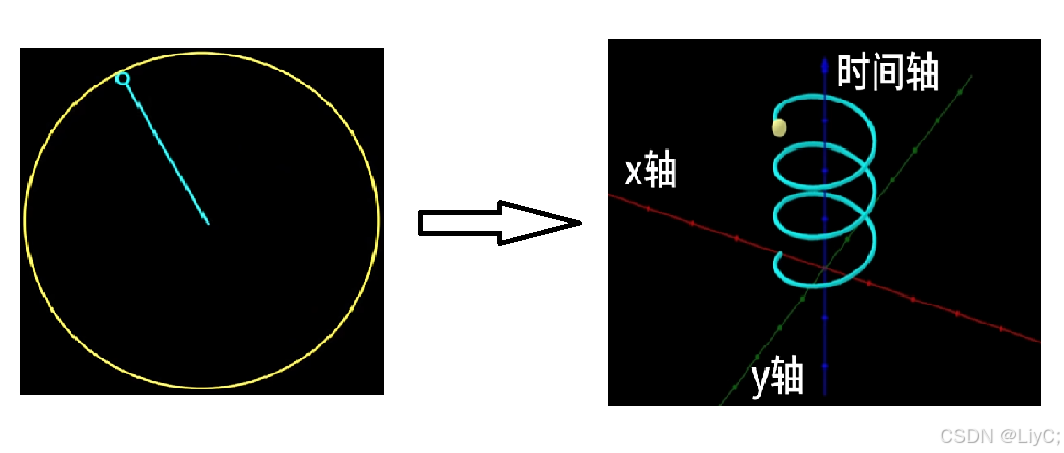
举例: 构造三个简单的旋转,叠加成一个复杂函数:
对于一个绕着中心点转圈的点(半径为3,转速1秒1圈),- 我们给它加上一个正交的时间维度,就会得到右图的圆柱螺旋线。
![1000070292]()
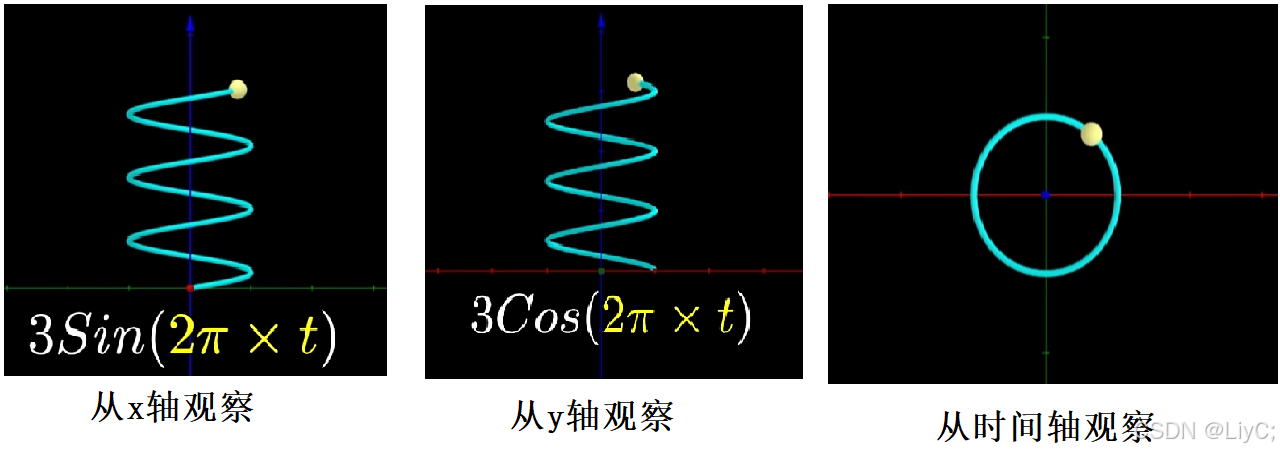
在这个空间,我们从不同角度观察会得到不同的曲线。
![1000070290]()
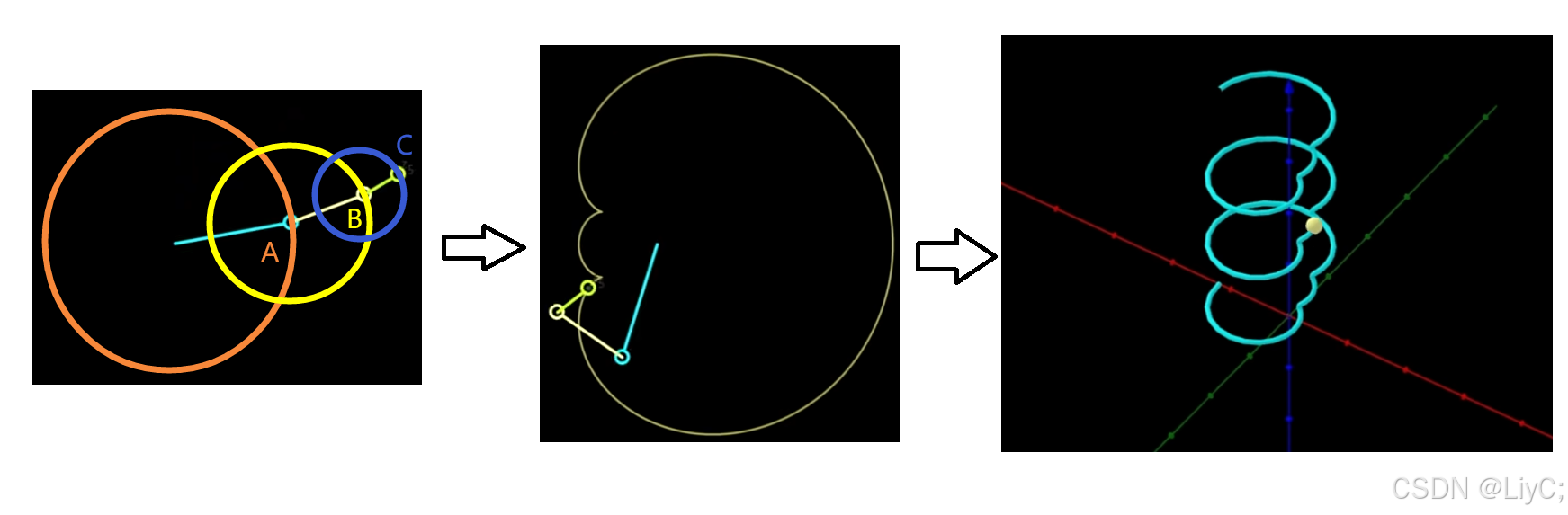
- 在以上的基础上,我们假设:
A点绕着中心 旋转(半径为3,转速1秒1圈),
B点绕着A点 旋转(半径为2,转速1秒2圈),
C绕着B点 旋转(半径为1,转速1秒4圈)。
最终得到的平面观察图如下。 同时再加上时间维度。
![1000070293]()
从三个不同的方向观察得到的结果如下:
![1000070294]()
- 我们给它加上一个正交的时间维度,就会得到右图的圆柱螺旋线。
-
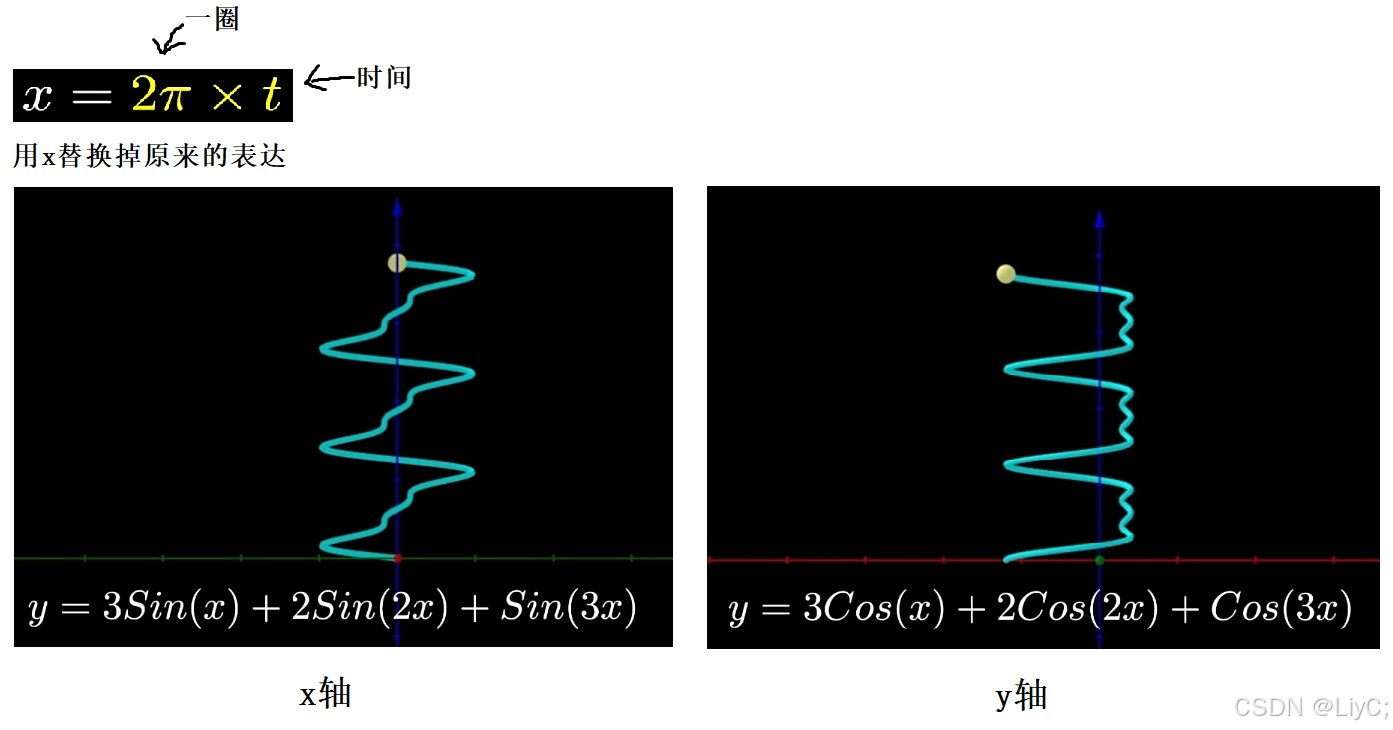
Fourier Series就是无穷多项的叠加。其公式如下(欧拉公式及其证明,文后有链接):
![1000070291]()
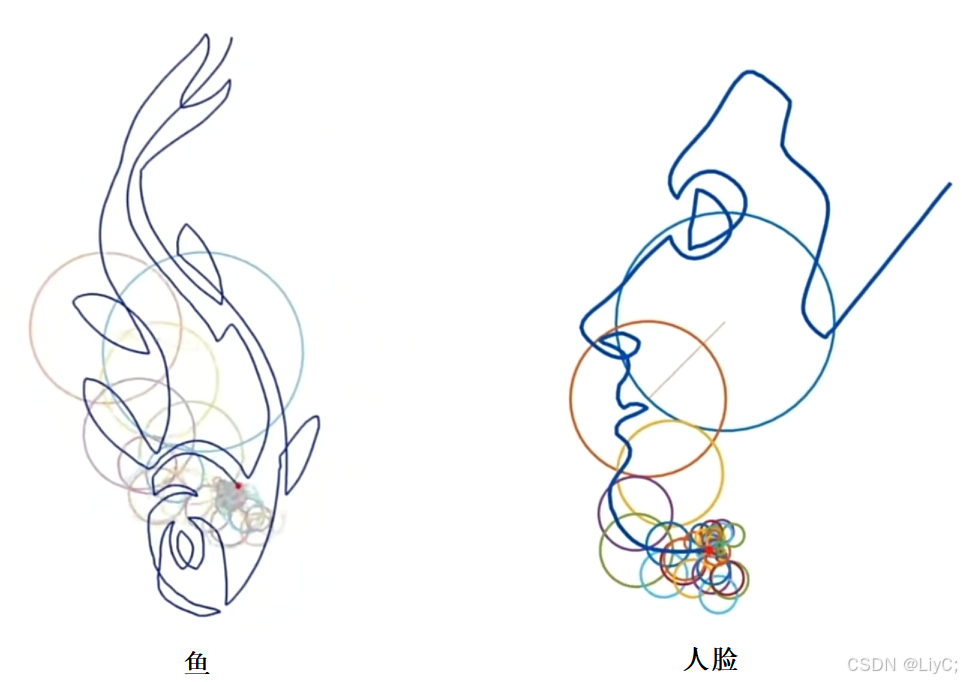
这个公式的几何表示,是用无限个圆盘一个接一个套在一起,每个都周期旋转;总体终点的轨迹,就可以表示任何函数图案,如下图:
![1000070289]()
Hilbert Space(希尔伯特空间)
Hilbert Space是Euclidean Space的直接推广,内积空间的完备化就是Hilbert Space。
-
Linear Space(线性空间)
Linear Space(线性空间), 就是在数域F上的Vector Space,定义加法和数乘两种运算,
向量空间的任何一个元素可以由其他元素线性表出,这就是线性空间。 -
Inner Product Space(内积空间)
在Linear Space(线性空间)的基础上, 定义了Inner Product(内积, 即点乘、标积)。
内积可以理解为:输入两个向量输出一个数的运算。
内积运算,在输入两个"向量型变量"时:输出就成了一个函数(因变量,数域F上的一个变化的数)。 -
Hilbert Space(希尔伯特空间)
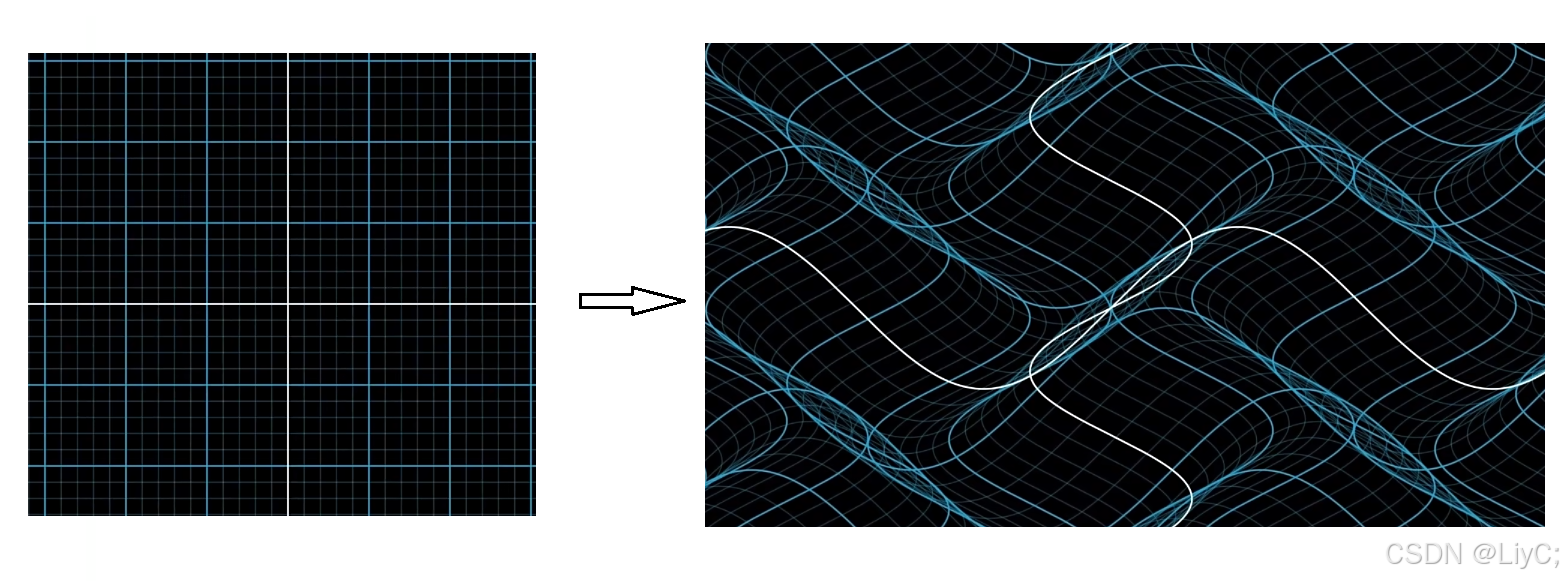
在常见的Vector Space(向量空间)坐标系上(y=0做x轴, x=0做y轴)进行改变,- 改成 sin(x) 做x轴,sin(2x) 做y轴。如下图:
![1000070296]()
- 在此基础上继续增加一个sin(3x)作为z轴,最后得到的三维空间如下图:
![1000070297]()
- 看起来很乱,先别担心,我们以\([1,1,1]\)为例,则它表达的向量是:
![1000070298]()
- 这和Fourier Series有点熟悉。当我们把它升到无穷维就会得到Fourier Series的正弦形式:
![1000070299]()
- 这代表几乎所有连续函数都可以这样分析,因为Fourier Series可以合成分解几乎所有其它函数。
以上 Inner Product Expression, 右边是一个f(x)函数,左边是一个 无限维空间的 向量
Hilbert提出, 把任意连续函数直接看成矢量,于是就可以把它拉成平直坐标系。
并且,这的所有的连续函数,就构成了一个完备的Euclidean Space。
任何一个函数,都可以对应成一个非常有规律的无限维空间的 一个向量。
![1000070300]()
- 改成 sin(x) 做x轴,sin(2x) 做y轴。如下图:
Hilbert Space就是完备化的Inner Product Space(内积空间),即其中任意柯西序列都收敛于该空间中的一个元素。
换一种表达,对于一个完备的内积空间,任何收敛序列都有极限存在于该空间。
这个性质在数学上非常重要,因为它保证了空间的序列不会收敛到“空间之外”,
进一步,使得我们可以更好地研究空间的性质和结构。
总结
- 欧式空间的应用场景很好理解,因为我们生活的就是一个三维的欧式空间,
我们常规理解的距离,长度,夹角的概念就是欧式空间的距离,范数,內积的定义。 - 希尔伯特空间的应用场景:
Hilbert Space的元素一般是函数,因为一个函数可以视为一个无穷维的向量。
如果大家熟悉 Fourier Transform或者Taylor Equation,便能自然推导空间的基底。
没错,也是非常有规律的一组无限多的函数。




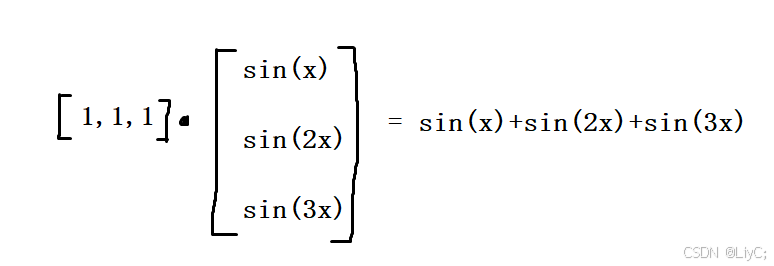
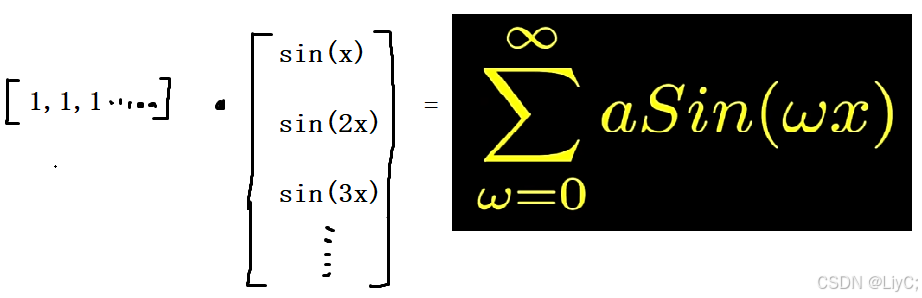

 浙公网安备 33010602011771号
浙公网安备 33010602011771号