SciTech-Mathmatics - Advanced Linear Algebra: 矩阵乘法 的 四种理解方式 + 向量 的空间&基、坐标&坐标变换 + Eigenvalue Decompression(特征值分解) + SVD(奇异值分解, Singular Value Decomposition)
SciTech-Mathmatics - Advanced Linear Algebra(高等线性代数):
矩阵乘法 的 四种理解方式
矩阵乘法有四种理解方式:
- 线性方程组视角:将矩阵看作行向量与向量的点积。
- 列向量观点视角:将矩阵分解成列向量的线性组合。
- 向量变换视角:将矩阵看作向量的变换函数。
- 坐标变换视角:将矩阵乘法理解为同一向量在不同坐标系下的表达方式。
背景: 线性方程组 + 消元法 + 初等行变换
矩阵诞生于线性方程组的求解,最基本的运算方法来自于高斯消元法,
所以矩阵整个运算规则都符合高斯消元法,矩阵源于 线性方程组,
但经过几十年的发展已不限于求解线性方程组,可用于很多应用场景。
线性方程组如下所示:
四种视角理解
-
线性方程组视角(向量点积视角)
将线性方程组直接写成向量形式,如下所示:
\(\large \begin{array}{lll} \begin{pmatrix} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n\\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n\\ \cdots \\ a_{m1}x_1+a_{m2}x_2+ \cdots +a_{mn}x_n \\ \end{pmatrix}= \begin{pmatrix} y_1\\ y_2\\ \cdots \\ y_m \end{pmatrix} \end{array}\)可认为是 "矩阵的行向量" 与 "向量x" 的 点积(矩阵的行乘以向量的列):
\(\large \begin{array}{lll} \begin{pmatrix} a_{11}&a_{12}& \cdots &a_{1n}\\ a_{21}&a_{22}& \cdots &a_{2n}\\ \cdots \\ a_{m1}&a_{m2}& \cdots &a_{mn} \\ \end{pmatrix} \begin{pmatrix} x_1\\x_2\\ \cdots \\x_n \end{pmatrix}= \begin{pmatrix} y_1\\ y_2\\ \cdots \\ y_m \end{pmatrix} \end{array}\) -
列向量观点视角
对于\(\large Ax=y\):
\(\large \begin{array}{lll} \begin{pmatrix} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n\\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n\\ \cdots \\ a_{m1}x_1+a_{m2}x_2+ \cdots +a_{mn}x_n \\ \end{pmatrix}= \begin{pmatrix} y_1\\ y_2\\ \cdots \\ y_m \end{pmatrix} \end{array}\)可以分解成:
\(\large \begin{array}{lll} \begin{pmatrix} a_{11}\\ a_{21}\\ \cdots \\ a_{m1}\\ \end{pmatrix}x_1+\begin{pmatrix} a_{12}\\ a_{22}\\ \cdots \\ a_{m2}\\ \end{pmatrix}x_2+\begin{pmatrix} \cdots \\ \cdots \\ \cdots \\ \cdots \\ \end{pmatrix}x_{ \cdots }+\begin{pmatrix} a_{1n}\\ a_{2n}\\ \cdots \\ a_{mn}\\ \end{pmatrix}x_n = \begin{pmatrix} y_1\\ y_2\\ \cdots \\ y_m \end{pmatrix} \end{array}\)上述就表示 向量\(\large y\) 是否能由 向量\(\large a\) 的 线性组合 得到,
只要向量\(\large y\)位于向量\(\large a\)张成的向量空间,那么向量\(\large y\)一定能由向量\(\large a\)线性组合得到,
即一定能找到一组\(\large x\)使得上式必然成立。 -
向量变换视角(矩阵函数)
对\(\large Ax=y\): 矩阵\(\large A\)使 向量\(\large x.\) 作 拉伸、旋转两种变换变成向量\(\large.y\),写成函数形式:\[\large f(x)=Ax \]矩阵乘法 𝐴𝑥 可理解为 矩阵\(\large A\) 作为一个 "线性变换函数", 将输入向量 𝑥
映射到一个新向量 𝐴𝑥。
对于一个 \(\large m×n\) 的矩阵 \(\large A\):- 定义域: 所有 n维向量的集合,即\(\large \bf{R}^n\);
- 值域: 可从 "矩阵乘法的列观点" 视角,值域\(\large \bf{R}^m\)。
通过矩阵函数(在矩阵的作用下),研究:
- 定义域 与 值域 的 映射关系,
如\(\large A\)是一个\(\large m \times n\)的矩阵,\(\large x\)是一个n维向量,
那么值域可认为是由\(\large A\)的n个列向量张成的空间,
张成的空间的维数等于列向量组的秩(小于等于n),即值域的维数一定是小于等于定义域的维数。
通过函数视角, 可研究在矩阵\(\large A\)有什么特征下, 定义域\(\large x\)与值域\(\large y\)的关系(满/单 射特性)。 - 矩阵函数(线性变换函数)的分解与合成:
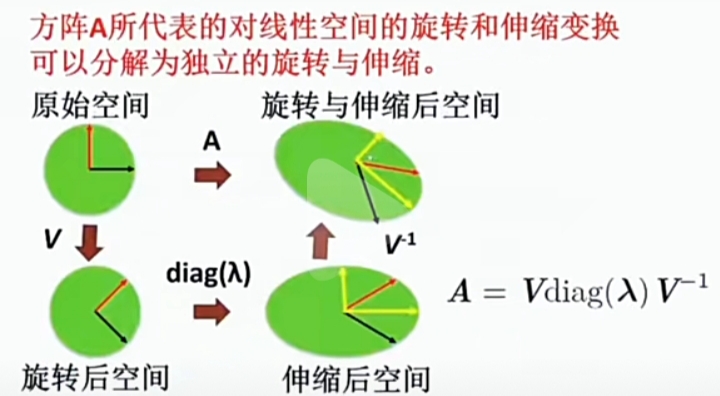
- 任何一个"矩阵(函数)"都可分解为“伸缩与旋转”两种基本的“矩阵函数(线性变换函数)”。
- 用“伸缩与旋转”两种基本的“矩阵函数(线性变换函数)”可合成任意目标矩阵(函数)。
- 伸缩(基本线性变换矩阵): 特征值,
- 旋转(基本线性变换矩阵): 等效于 “坐标系变换(换坐标系)”,
-
坐标变换视角
对于同一个向量在不同基(即为不同坐标系)下有不同的坐标值,
虽然 坐标值不同, 但都表达 同一向量,即它们的方向和长度完全一致,
对于 "矩阵向量的乘法", 可以认为是 "同一个向量" 在 不同的坐标系的表达,
当然就可以由 "正向变换" 与 "逆向变换" 两个角度去理解矩阵乘法。对于\(\large Ax=y\)可以有两个坐标变换的视角,
-
一个视角是向量\(\large x\) 自然基坐标,另外一个是非自然基坐标。
对于向量\(\large x\)为非自然基坐标,向量\(\large y\)为自然基坐标,
向量\(\large x\)可以理解为以矩阵\(\large A\)的列向量为基的非自然坐标系坐标,
那个\(\large Ax\)运算即为将 向量\(\large x.\)转换到自然系的向量\(\large y\)的坐标。
\(\large \begin{array}{lll} Ax=\begin{pmatrix} a_{11}\\ a_{21}\\ \cdots \\ a_{m1}\\ \end{pmatrix}x_1+\begin{pmatrix} a_{12}\\ a_{22}\\ \cdots \\ a_{m2}\\ \end{pmatrix}x_2+\begin{pmatrix} \cdots \\ \cdots \\ \cdots \\ \cdots \\ \end{pmatrix}x_{ \cdots }+\begin{pmatrix} a_{1n}\\ a_{2n}\\ \cdots \\ a_{mn}\\ \end{pmatrix}x_n \\ = y_{1} e_{1} + y_{2} e_{2} + \cdots + y_{n} e_{n} \end{array}\) -
坐标变换的另外一个角度,是认为\(\large x\)是自然基坐标系,即:
\(\large \begin{array}{lll} x=\begin{pmatrix}x_1 \\x2\\ \cdots \\x_n\end{pmatrix} = E*\begin{pmatrix}x_1 \\x2\\ \cdots \\x_n\end{pmatrix} \\ = x_1\begin{pmatrix}1\\0\\ \cdots \\0\end{pmatrix}+ x_2\begin{pmatrix}0\\1\\ \cdots \\0\end{pmatrix}+ \cdots + x_n\begin{pmatrix}0\\0\\ \cdots \\1\end{pmatrix}\\ \ \\=x_1e_1+x_2e_2+ \cdots +x_n e_n \\ = y_1 A^{-1}_{1} + y_2 A^{-1}_{2} + \cdots + y_n A^{-1}_{n} \\ A^{-1} = (A^{-1}_{1}, A^{-1}_{2}, \cdots , A^{-1}_{n}) \end{array}\)
用\(\large Ax\)视角观察, 并不能直观地观察到坐标变换规律,可将其做一个简单变形:
\(\large \begin{array}{lll} Ax=y\ \rightarrow \ x=A^{-1}y \end{array}\)
上式的\(\large x\)是自然基坐标系,\(\large y\)是非自然基坐标系,
\(\large Ax\)就将自然基坐标, 转换成以\(\large A^{-1}\)的列向量为基坐标系的坐标。
矩阵向量乘法\(\large Ax=y\),一定情况下可认为:
向量\(\large x\)与向量\(\large y\)为同一向量,仅仅是坐标系不同,
"一定情况下"指 "\(\large A\)为满秩矩阵",因为 \(\large A\)为 非满秩矩阵就可能出现 "降维" 情况。
-
向量 的空间&基、坐标&坐标变换
 |
 |
 |
|---|---|---|
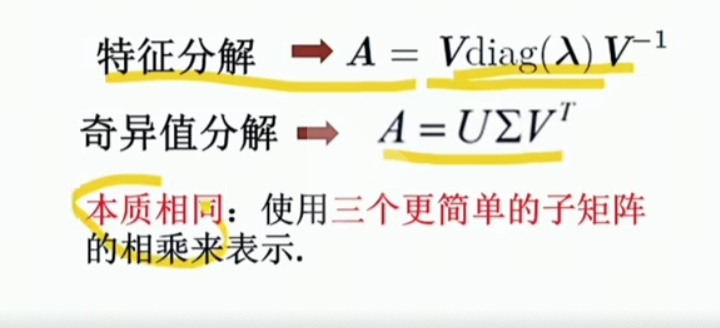
Eigenvalue Decompression(特征值分解)
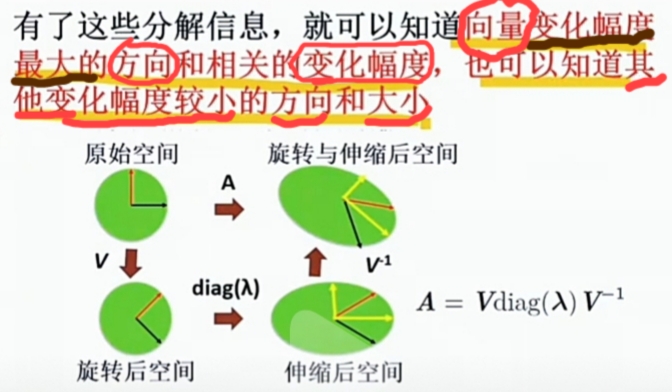
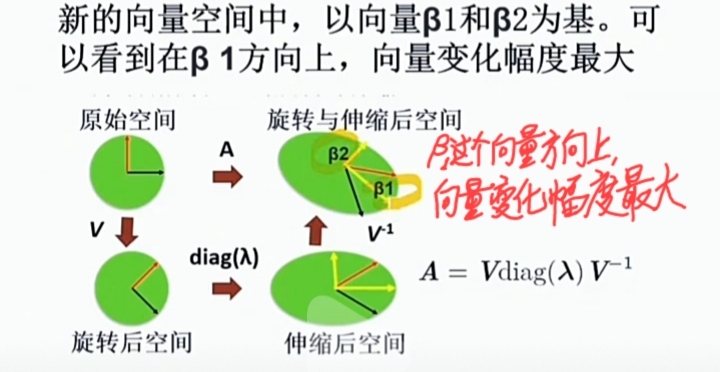
特征分解的本质之一: 利用分解结果生成新的向量空间
 |
 |
 |
|---|---|---|
 |
 |
 |
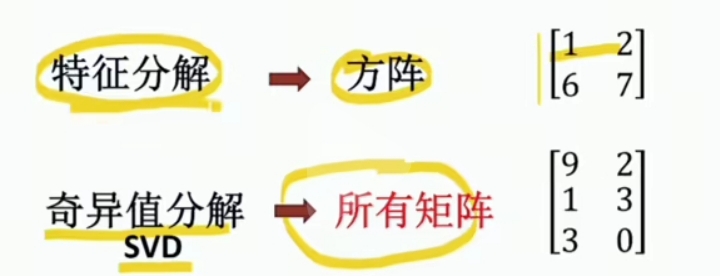
SVD(奇异值分解, Singular Value Decomposition)
 |
 |
 |
|---|---|---|



 浙公网安备 33010602011771号
浙公网安备 33010602011771号