SciTech-Logic:逻辑学-Introduction to Logic: Irvine - 5.2 Class and Statement 类与直言命题

类与直言命题
亚里士多德三段论逻辑，主要探讨的是关于不同对象类之间相互关系的论证。

Class:类

• Class类，指的是共有certain specific property:某种特定属性的objects:所有对象的collection:汇集。
  第3章在解释词项内涵的定义时，已经简单地介绍过"class:类"这个概念。

Relations of Classes(类之间的关系)

任何人都能立刻明白两个类至少可以有如下三种相互关系(这三种关系适用于任何类或范畴)。：

1. wholly included(or wholly contained):
   如果一个类的所有元素都是另一个类的元素，则称:
   第一个类wholly included(包含于)或wholly contained(包括在)第二个类；
   例如人的类与哺乳动物的类.
2. partially included:
   如果一个类的一部分元素但不是所有元素都是另一个类的元素，则称:
   第一个类partially included(部分地包含于)第二个类；
   例如运动员的类和女人的类.
   3.exclude:
   如果两个类没有共同的元素，则称: 这两个类之间是互斥(exclude)的。
   例如三角形的类和圆形的类.

直言命题

Definition of 直言命题 的 定义
在本章的演绎论证，我们给出的命题都是陈述某个类与另一个类的关系，这种命题被称为直言命题。

在演绎逻辑的传统解释，直言命题是演绎逻辑的基本要素和论证的组成部分。

论证（基于 直言命题 ）

考虑如下论证：

• 没有运动员是素食主义者，
• 所有足球队员都是运动员，

• 所以，没有足球队员是素食主义者。
  以上论证的三个命题都是直言命题。

当然我们可能怀疑其前提的真，但是：

• 上述例子的三个直言命题是关于所有运动员的类、所有素食主义者的类和所有足球队员的类。
• 这些命题所表达的类与类的关系产生一个肯定有效的论证：
  如果这些前提为真，则结论必定为真。
• 以上的两个前提都是直言命题，即它们都肯定或否定某个类S全部或部分地包含于另外一个类P。
• 其实，还有一个隐含的“World Knowledge(世界知识)”: “所有的足球队员 都是 运动员”，形式化的表达是“所有足球队员的类，都Wholly included(包含于), 所有运动员的类”.
  只是 “Axiom(公理, 举世公认的 或 不言而喻的)”为全世界的人们所熟知，而略去不表。

演绎论证(以class:类 为基础的)

因此，要建立一种以class:类为基础的演绎理论，关键性的第一步就是确认直言命题的种类，深一步揭示出这些直言命题的相互关系。

直言命题的Category(种类)

5.3　四种直言命题
有且只有四种标准直言命题，可分别由如下命题示例：

1. 所有政客是说谎者。
2. 没有政客是说谎者。
3. 有政客是说谎者。
4. 有政客不是说谎者。

下面我们依次对这四种直言命题加以解释。

1.全称肯定命题

断言****第一个类的所有元素 都是 第二个类的元素。
举例:“所有政客是说谎者”断言政客类的所有元素都是说谎者类的元素。
所有全称肯定命题都可以写成如下标准形式：

所有S是P (字母S和P分别代表主项和谓项)。

这样的命题不仅断言两个类之间的包含关系，而且断言这两个类之间的包含关系是完全的或普遍的。S的所有元素都被断定为P的元素。这种标准形式的命题被称为全称肯定命题，也叫A命题。

直言命题 的 图形表达

直言命题通常用图形表达，用两个交叉的圆代表涉及的两个类。这种图形称为文恩图(Venn diagram)，得名于发明者英国数学家、逻辑学家约翰·文恩(John Venn,1834—1923)。也将会看到其对评估演绎论证有效性的巨大作用。
稍后我们将详细介绍这种图示方法，目前我们只用文恩图来图示每一类直言命题的含义。我们：

• 用一个圆S表达主项所代表的类，
• 用另一个圆P表达谓项所代表的类。
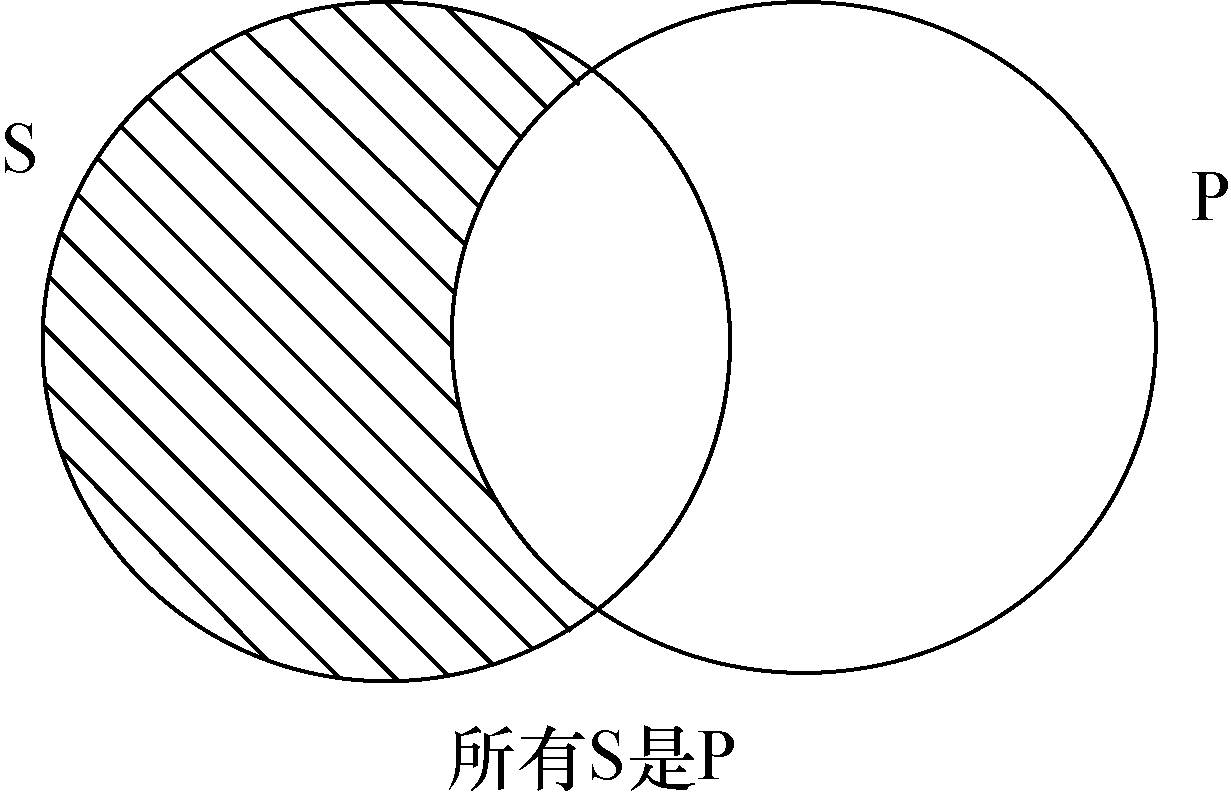
• A命题断言所有S是P。A命题的图示如下：
  注意: 圆P之外的S部分 要画上阴影，以表明S的元素没有不是P的元素。
  

2.全称否定命题

上面的第二个例子“没有政客是说谎者”无例外地否认了政客类的任何元素是说谎者类的元素。
它断言主项S类与谓项P类是完全相互排斥的。这种直言命题可以标准地写为：
没有S是P( S和P分别代表主项和谓项)。
这种命题完全否认两个词项之间的包含关系。它告诉我们，没有S的元素是P的元素。
这种标准形式的命题被称为全称否定命题，也称为E命题。

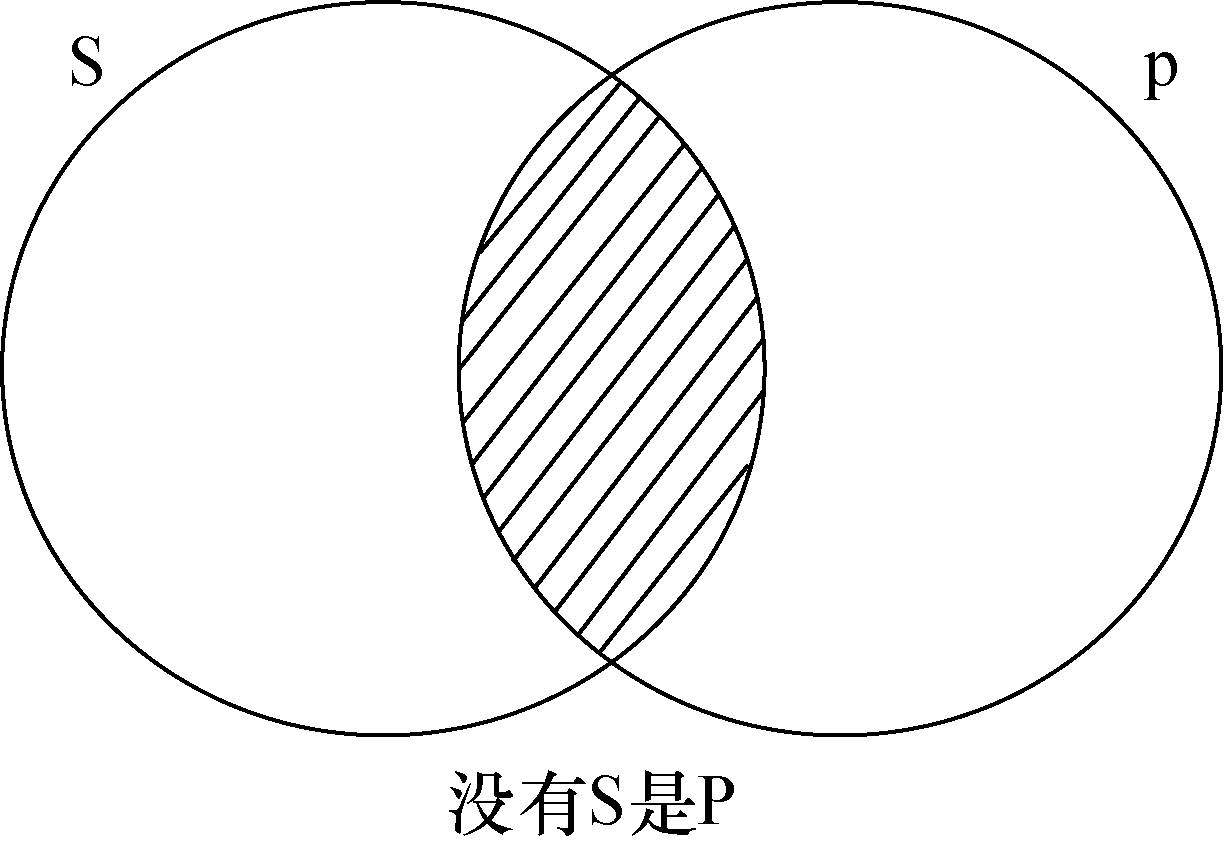
E命题的文恩图

E命题的文恩图是将代表S类和P类的两个圆的交叉部分画上阴影，以表示S类与P类相互排斥。
于是，E命题可以图示如下：

3.特称肯定命题

上述第三个例子“有政客是说谎者”断言所有政客类的某些元素是所有说谎者类的元素。
但是它并没有对所有政客进行断定，仅仅断言了某一政客或某些政客是说谎者。
该命题既没有对所有政客做任何全称的肯定或否定，没有做出对政客的全体元素的断言，也没有断言有些政客不是说谎者，尽管在某些语境下该命题被认为暗含这种含义。该命题字面的意思和准确的释义，就是断言政客类和说谎者类有某些相同的元素。这就是我们需要明确的这类标准命题的含义。

• “some(有些)”是一个不确定的术语。
  它的意思是“至少有一个”、“至少有两个”还是“至少有一些”？“有些”究竟意味多少？
  在日常谈话，语境可能会影响我们对该术语的理解。
• 但是逻辑学家出于对Certainty(确定性)的考虑，将"some(有些)"解释为"至少有一个,但不是全部", 以与A命题 和 E命题 作 严格区分。
• 特称肯定命题可以写为如下标准形式：

  有S是P。
  它断言至少有一个S（用以标示主项类）的元素也是谓项类P的元素。
  该命题断言类的包含关系部分地成立，即对第一个类中的某个或某些特殊元素做出断言。
  这种标准形式的命题被称为特称肯定命题，也叫I命题。

• 在两个圆的交叉部分标一个x，表明至少有一个个体既是S的元素又是P的元素，我们便得到I命题的图示：
  

4.特称否定命题

上述第四个例子“有政客不是说谎者”跟第三个例子一类，
并没有全称地指称政客类，只是指出了该类的某个或某些元素，所以它是特称的。
但是与第三个例子不同，它没有断定第一个类的某个或某些元素包含在第二个类，那正是它所否认的。
该类命题被写成如下标准形式：

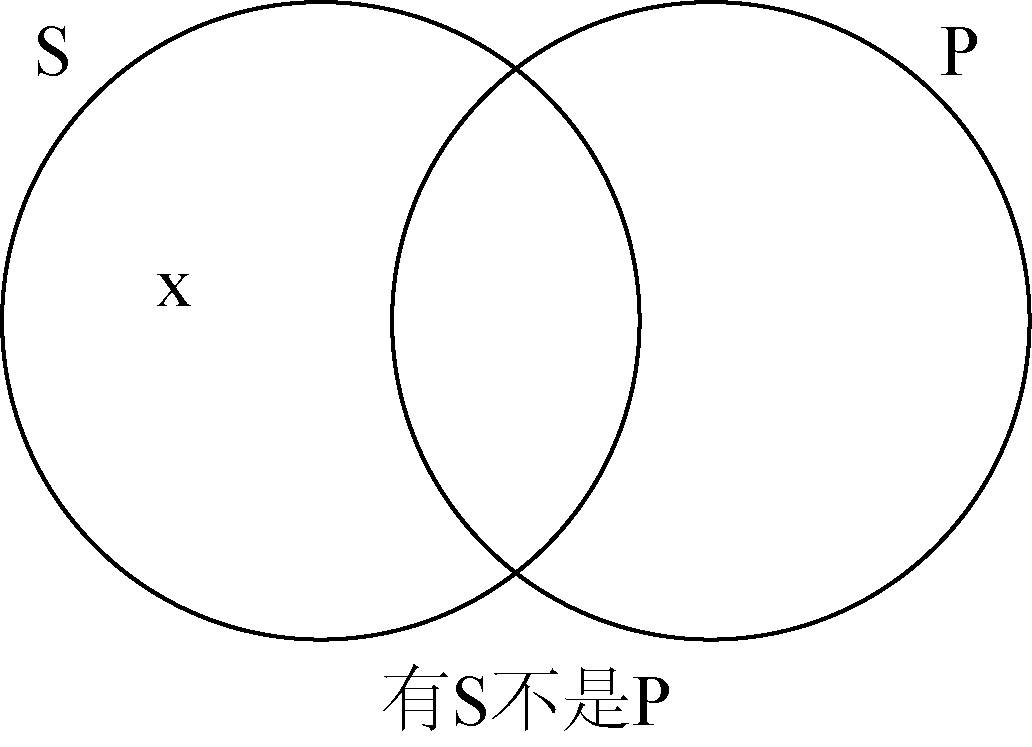
有S不是P。

它断言主项类S，至少有一个元素排除在谓项类P的全部元素之外。该否定不是全称的。
这种形式的命题被称为特称否定命题，也称O命题。
在P以外的S部分标一个x，表示至少有一个S的元素x不是P的元素，我们便得到O命题的图示：

上述例子中，所有的类都被简单地命名为：政客、说谎者、素食主义者、运动员等。
但是标准直言三段论的S主项和P谓项也许更为复杂。
举例来说，在命题“所有这个职位的候选人都是诚实而正直的人”，
主项是“这个职位的候选人”，谓项是“诚实而正直的人”。
主项和谓项还可以更为复杂，
但是所有标准直言命题所表达的都是S(主项)所代表的类与P(谓项)所代表的类之间的关系。
这四种命题——A、E、I、O——是演绎论证的组成部分。

上述对直言命题的分析看起来简单直接，但对这些命题的基础作用及其相互关系的挖掘却是逻辑体系发展史的一大步，也是亚里士多德对人类知识的巨大贡献之一，不要被表面的简单性迷惑。
正是在对象的类以及类的关系的基础之上，逻辑学家们通过几个世纪，建构出分析演绎论证的精致系统。该系统精细而透彻，是人类最伟大的智慧结晶之一。

我们将按照以下三个步骤对该系统进行研究：

• A.在本章余下部分我们将更加深入地考察标准直言命题的特点，解释它们之间的相互关系，探究从这些直言命题能够直接得出的推论是什么。我们将会看到，仅仅把握A、E、I、O命题及其相互关系，就能够掌握大量的演绎推理。
• B.在下一章，我们将要考察的是三段论，即通常由标准直言命题构成的论证。在那里，我们将揭示出三段论的实质，展示出每一种有效三段论形式的独特性质，并由此给予它们相应的名称，然后再介绍验证三段论有效性（或者无效性）的强有力方法。
• C.在第7章，我们结合日常论证的语言对三段论推理进行考察。这种结合会暴露出三段论推理的某些局限，但正是这种结合将显示出三段论的广泛应用。