SciTech-Mathmatics-Analysis: Bouncing Function(震荡函数, 导数±震荡)：L'Hospital + 点导数 + 导数 + 连续 + 极限 + 领域 +

SciTech-Mathmatics-Analysis:

考研易错概念:

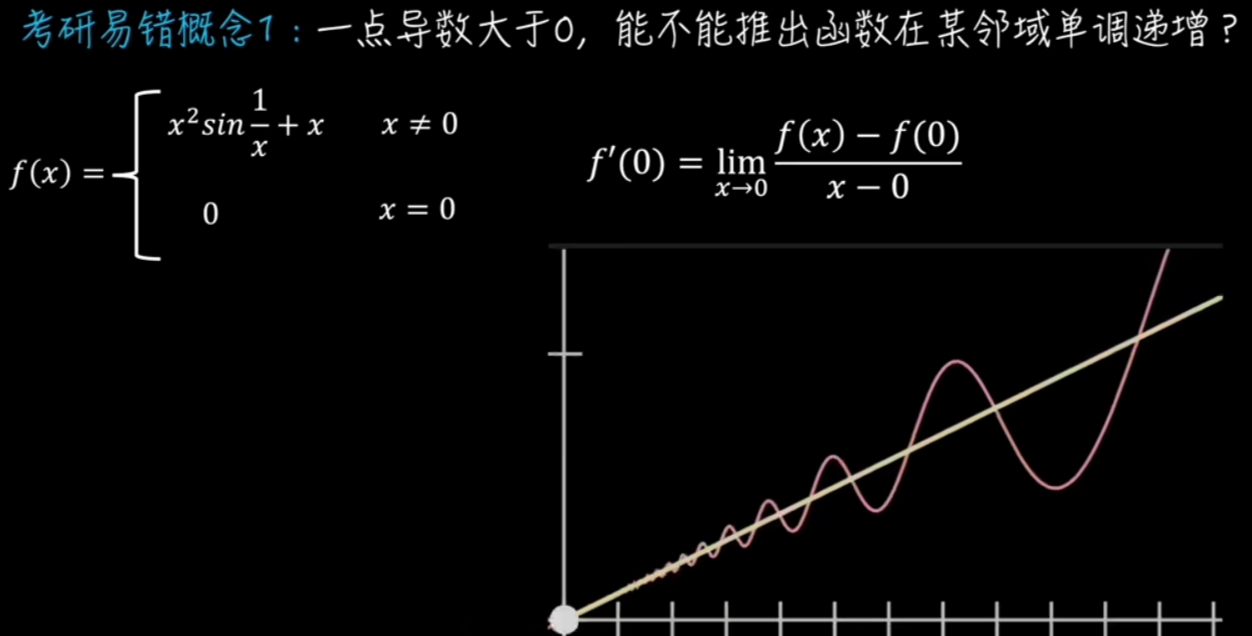
1. 一点的导数大于0, 能不能推出函数在某邻域单调递增? ✘
2. 无穷小的倒数,一定为无穷大? ✘
3. \(\large L'Hospital\) 的前提条件 及 何时为何失效? ✘
4. 不连续的函数,一定没有原函数? ✘
5. \(\large \underset{x \rightarrow x _0}{\lim} {f(x)=u_0}, \ \underset{u \rightarrow u_0}{\lim} {g(u)=A}\), 则 \(\large \underset{x \rightarrow x _0}{\lim} {g(f(x))=A}\) ? ✘
6. \(\large f(x)\) 连续, \(\large \underset{x \rightarrow x _0}{\lim} {f'(x)=A}\) => $\large f'(x_0)=A $ ? ✘

Instance of Bouncing Function

震荡函数(导数±震荡):
\(\large \begin{array}{lrl} \\ f(x) = x^2 \sin{(\frac{1}{x})} + x & x \neq 0 \\ \\ \end{array}\)

\(\large L'Hospital\) + 点导数 + 导数 + 连续 + 极限 + 领域 +