SciTech-Mathmatics-Analysis: important inequalities 重要的几个不等式: Trigonometry + Mean + Cauchy + Minkowski + Newton + Bernoulli + Chebyshev + Hölder

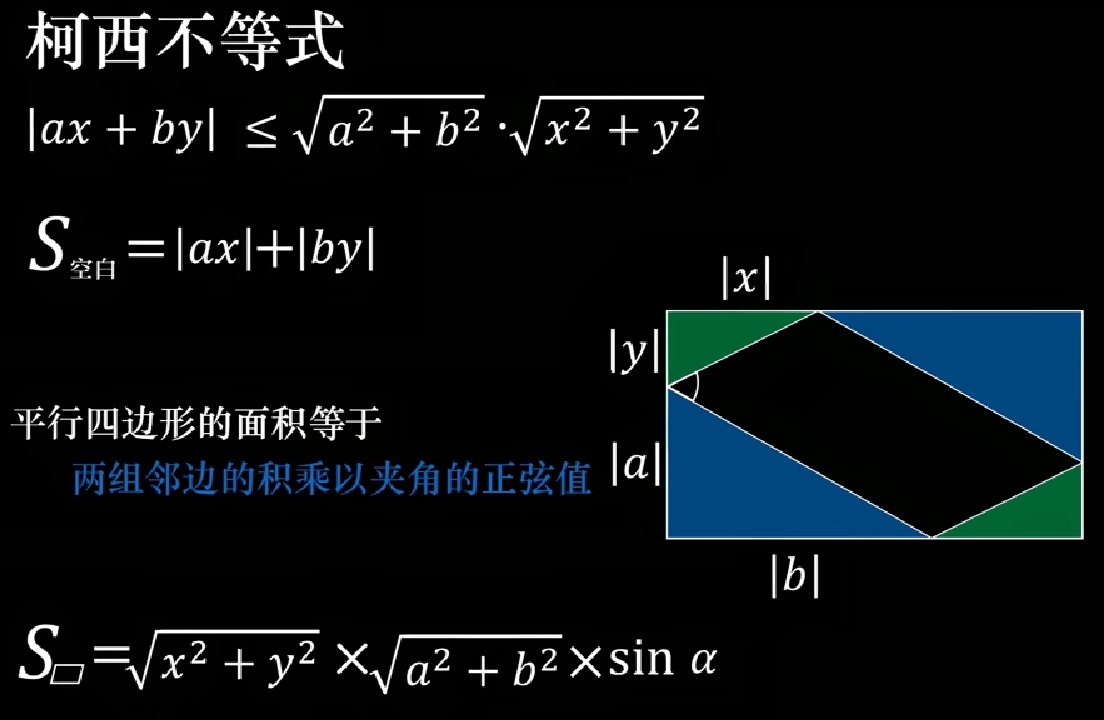
  • Cauchy Inequality(柯西不等式):

\(\large \begin{array}{rl} \\ | ax +by | &<= & \sqrt{a^2+b^2} \cdot \sqrt{x^2+y^2} \\ & \because & | ax +by | \leq |ax| + |by| = \sqrt{a^2+b^2} \cdot \sqrt{x^2+y^2} \cdot \sin{\alpha} \\ \end{array}\)




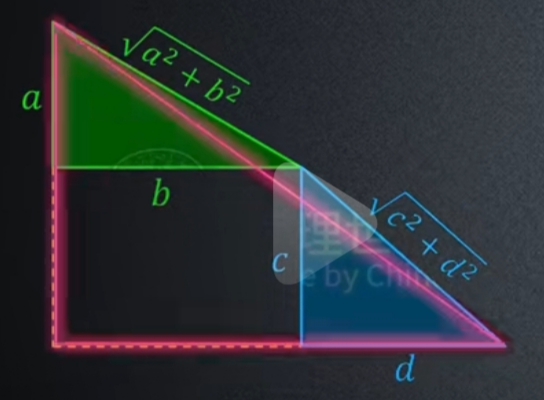
  • Minkowski inequality

$\large \sqrt{a^2 + b^2} + \sqrt{c^2 + d^2} \geq \sqrt{(a+c)^2+(b +d)^2} $



  • 权方和 inequality




  1. 均值不等式

\(\large Q_n = \dfrac{ a_1 + a_2 + \cdots + a_n } {n}, \text{ 算数平均数 }\)
\(\large Q_n = \sqrt{ \dfrac{ a_1^2 + a_2^2 + \cdots + a_n^2 } {n} }, \text{ 平方平均数 }\)



  1. 排序不等式




  1. Trigonometry inequality




  1. Newton inequality




  1. Bernoulli inequality




  1. Chebyshev inequality



  2. Hölder Inequality



posted @ 2024-08-23 18:16  abaelhe  阅读(23)  评论(0)    收藏  举报