Math-Derivative导数-夹逼定理:常用的不等式放大缩小 + log对数的妙用:将 嵌套的 指数运算 转换为 指数的乘法 与 将 幂函数 的 乘法 转换为 指数的加法运算
https://zhuanlan.zhihu.com/p/396423540
1. (A**b)**(c) = A**(b * c) # 将 指数运算的嵌套 转换 为 指数的 乘法运算
2.(A**b) * (A**c) = A**(b + c) # 将 幂函数的乘积 转换为 指数的 加法运算, 同底数型
3.(A**b) * (D**c) = (e**(blnA)) * (e**(clnD)) = e**(blnA + clnD) # 不同底数型,都换成自然常数 e 为底数的,进行上式转换
Q**n = (e**(lnQ))**n = e**(n*lnQ)
直观图解36个放缩常用不等式:
- 指数函数放缩:
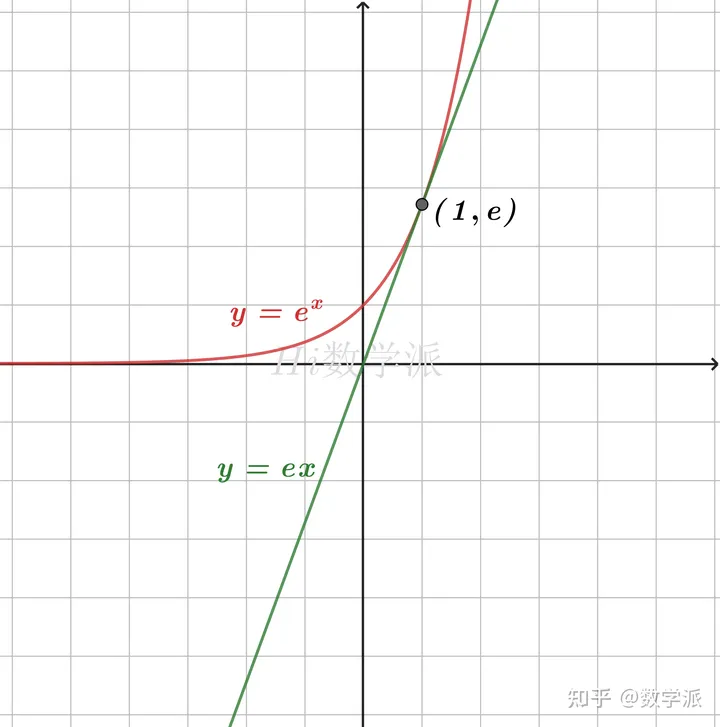
自然常数e作为底数时, 放缩成 一次函数,
自然常数e作为底数时, 单调递增,经过(0,1)点, 任何高阶导数 都为 e**x 并且也都经过(0, 1)点.
当x=0 时 E**x = x + 1, 而E**x的导数在x=0以外的 任何一点x 都大于 0
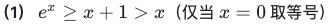 |
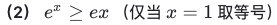 |
|---|---|
 |
 |



 浙公网安备 33010602011771号
浙公网安备 33010602011771号