条件概率:{乘法公式•全概率公式•Bayes公式}_Bayes: PosteriorP(A|B)=PriorP(A)•Likelihood:(P(B|A)/P(B))

条件概率的三种形式

This can also be stated as P (A | B) = P(A) • (P (B | A) / P(B) , where P(A|B) is the probability of A given B, also called posterior

  • Prior: Probability distribution representing knowledge or uncertainty of a data object prior or before observing it
  • Posterior: Conditional probability distribution representing what parameters are likely after observing the data object
  • Likelihood: The probability of falling under a specific category or class.

  1. P(Y|X) = P(YX) / P(X):
    条件概率P(Y|X) 是集合 X与Y的交集XY占条件集X的比例。

  2. P(X)P(Y|X) = P(Y)P(X|Y) = P(XY)
    Y、X 是两个事件，存在某种程度上的相互联系:
    则由 Whole总体-Part局部、History历史-Current现在 的客观规律性;

    • P(Y): Empirical Info.( History/Whole ):
      经验概率, 来自理论, 总体普遍规律, 既有经验, 大范围统计, 历史时序数据)

    • P(X|Y): Likelihood Probability:
      似然概率(经验概率为前提, 普遍总体->群/样本集，历史->当前, 甚至是主观预估)

    • P(X):Practical Sampling Info. 样本概率(标准化常量: 因样本概率可处理成标准化常量)
      来源于 practice真实实践, sampling抽样得到Part局部/Current当前批次/时刻的样本

    • P(Y|X):后验概率(practical info.为前提)
      在实践得到的样本之上，以 计数原理/统计采样, 得到 P(Y|X)后验概率。

条件概率应用之分类器：

要从概率的角度处理分类器的问题：
   把 Y, X 视为随机变量(随机事件的结果集合),
      features: X =(X1, X2,…,Xn)， 有 n 个特征的向量;
      label: Y 属于结果集合{y1, y2, …, yn}

    则有条件概率(X为给定集合时, Y = y 的概率)表示为: 
      P(Y=y | X=(x1, x2, …, xn))

    Hypothesis:
      for what value of y,
        P(Y=y|X=(x1,x2,…,xn)) is maximum.
    But …,  P(Y|X) is hard to find.

    To address it, here we introduce Bayes Theorem.
        P(Y|X) = P(Y)•P(X|Y)/P(X)

    where the right side is our dataset .

Application of Bayes' Theorem: Naive Bayes Classifiers and their implementation
https://www.geeksforgeeks.org/naive-bayes-classifiers/

Naive Bayes classifiers are a collection of classification algorithms,
based on Bayes’ Theorem. It is not a single algorithm but a family of algorithms where all of them share a common principle, i.e. every pair of features being classified is independent of each other.

To start with, let us consider a dataset.
Consider a fictional dataset that describes the weather conditions for playing a game of golf.
Given the weather conditions, each tuple classifies the conditions as fit(“Yes”) or unfit(“No”) for playing golf.

Here is a tabular representation of our dataset.

The dataset is divided into two parts, namely, feature matrix and the response vector:

  • Feature matrix contains all the vectors(rows) of dataset in which each vector consists of the value of dependent features. In above dataset, features are ‘Outlook’, ‘Temperature’, ‘Humidity’ and ‘Windy’.
  • Response vector contains the value of class variable(prediction or output) for each row of feature matrix. In above dataset, the class variable name is ‘Play golf’.

Assumption:
The fundamental Naive Bayes assumption is that each feature makes an:

  • independent
  • equal
    contribution to the outcome.

With relation to our dataset, this concept can be understood as:

  • We assume that no pair of features are dependent. For example, the temperature being 'Hot' has nothing to do with the 'Humidity' or the 'Outlook' being "Rainy" has no effect on the 'Windy'. Hence, the features are assumed to be independent.
  • Secondly, each feature is given the same weight(or importance). For example, knowing only temperature and humidity alone can’t predict the outcome accurately. None of the attributes is irrelevant and assumed to be contributing equally to the outcome.
    Note: The assumptions made by Naive Bayes are not generally correct in real-world situations. In-fact, the independence assumption is never correct but often works well in practice.

Now, before moving to the formula for Naive Bayes, it is important to know about Bayes’ theorem.

Bayes’ Theorem:
Bayes’ Theorem finds the probability of an event occurring given the probability of another event that has already occurred. Bayes’ theorem is stated mathematically as the following equation:

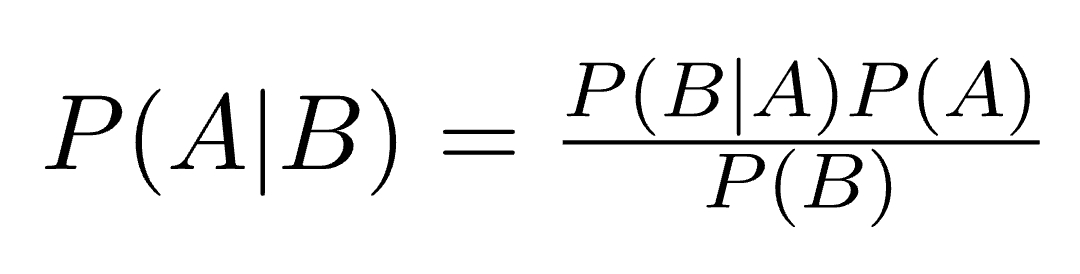
where A and B are events and P(B) ≠ 0.

Basically, we are trying to find probability of event A, given the event B is true.

  • P(A) is the priori of A (the prior probability, i.e. Probability of event before evidence is seen).
  • Event B is also termed as evidence. The evidence is an attribute value of an unknown instance(here, it is event B).
  • P(A|B) is a posteriori probability of B, i.e. probability of event after evidence is seen.

Now, with regards to our dataset, we can apply Bayes’ theorem in following way:

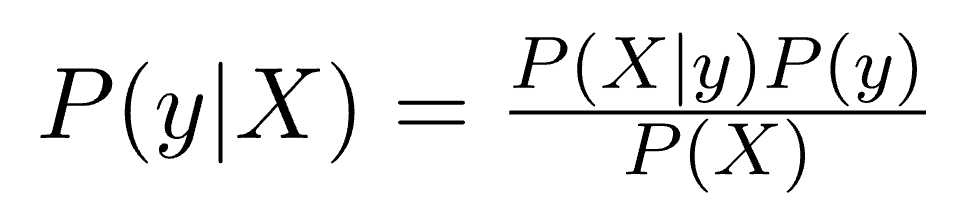
where, y is class variable and X is a dependent feature vector (of size n) where:

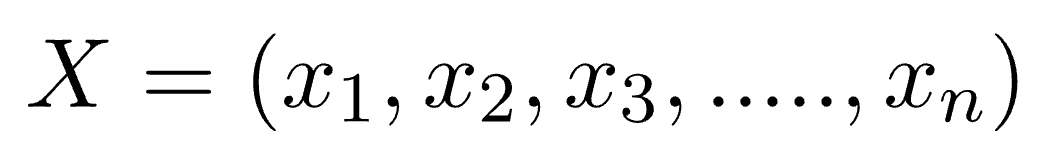
Just to clear, an example of a feature vector and corresponding class variable can be: (refer 1st row of dataset)

    X = (Rainy, Hot, High, False)
    y = No

So basically, P(y|X) here means, the probability of “Not playing golf” given that the weather conditions are “Rainy outlook”, “Temperature is hot”, “high humidity” and “no wind”.

Naive assumption
Now, its time to put a naive assumption to the Bayes’ theorem, which is, independence among the features. So now, we split evidence into the independent parts.

Now, if any two events A and B are independent, then,

P(A,B) = P(A)P(B)
Hence, we reach to the result:

which can be expressed as:

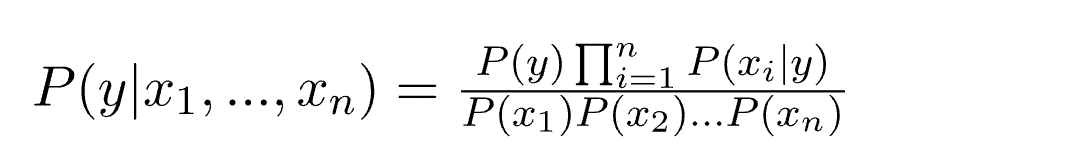
Now, as the denominator remains constant for a given input, we can remove that term:

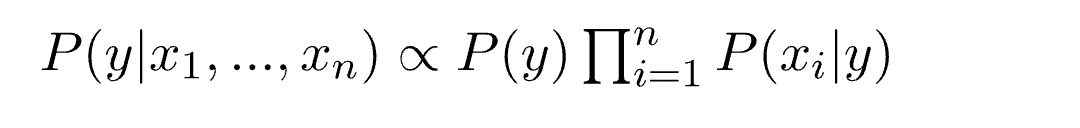
Now, we need to create a classifier model. For this, we find the probability of given set of inputs for all possible values of the class variable y and pick up the output with maximum probability. This can be expressed mathematically as:

So, finally, we are left with the task of calculating P(y) and P(xi | y).

Please note that P(y) is also called class probability and P(xi | y) is called conditional probability.

The different naive Bayes classifiers differ mainly by the assumptions they make regarding the distribution of P(xi | y).

Let us try to apply the above formula manually on our weather dataset. For this, we need to do some precomputations on our dataset.

We need to find P(xi | yj) for each xi in X and yj in y. All these calculations have been demonstrated in the tables below:

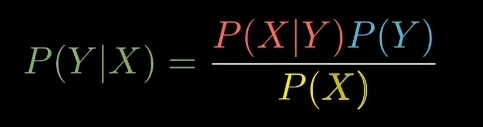
Bayes Theorem

posted @ 2023-07-07 10:25  abaelhe  阅读(231)  评论(0)    收藏  举报