数学邪修手册

数学邪修手册

前言

在中学数学，普遍存在这样一个问题：

你更擅长代数还是几何？

根据我们长时间的交流，男生大概率更喜欢代数，女生则偏向几何。不过，这种特征不是绝对的，也可能有同学两个差不多。

还有一个惊人的结论，就是如果一个人代数很好，那 ta 在做几何题时，很有可能想不出辅助线做法或者解题思路；如果一个人几何很好，那 ta 可能在理解代数概念和运算应用时遇到困难。

于是，有人说代数和几何之间是一条不可跨越的鸿沟。就如鱼和熊掌不可兼得一样，你几乎不可能同时完全精通代数和几何。

这个说法看上去没有任何问题。你难道会认为满屏的数字和满屏的点点线线之间有显然的联系吗？

显然的联系当然是没有的。不过，的确有一种在普通中学生眼中十分怪异的联系方法。并且，现在它已经被大大小小的中学生所接受，并运用这个怪异的方法解决了成千上万的问题。这种方法一开始只在高中用得较为频繁，而现在，许多初中生已经热衷于运用这种“超纲”的方法了。

这就是建系。全称是建立平面直角坐标系，你也可以叫它建系暴算或代数爆破。

如果你亲身体验过建系解决几何问题，你一定能够快速归纳出这个方法的优缺点。

• 优点：思路清晰简单，无脑算即可；数形结合，有时可以比几何方法更快。
• 缺点：计算量较大，计算基础不扎实的话，容易出错；需要提前了解一些代数知识。

为了让各位更好地掌握、驾驭数形结合的解题方法，我们撰写了这套《数学邪修手册》。如你所见，这套手册中的方法显然都不是正常方法，也就是所谓的“邪修”。

邪修方法可能不是最快的，但你必须承认，它一定是思维含量最低的，并且是最权威的。（意思是，在做题者的计算能力足够好的前提下，它可以保证答案正确。）并且，我们可以自信地说，建系可以解决几乎所有几何问题，并且可以秒杀大部分几何问题。

让我们开始吧！你可以选择在日常练习中不用建系，但它在中考中或许能保你几分呢。

第一章 坐标系中的圆

1.1 圆方程

经过老师的科普，我们已经大概了解，形如\((x-a)^2+(y-b)^2=c(c>0)\)的表达式可以表示一个圆。这个圆的圆心坐标就是\((a,b)\)，半径为\(\sqrt c\)。接下来，我们对这个方程变形，使你更容易理解为什么圆要用这个表达式。

两边同时开根号，有：

\[\sqrt {(x-a)^2+(y-b)^2}=\sqrt c \]

左边形式似曾相识，我们可以想到：

\[d_{AB}=\sqrt {(x_A-x_B)^2+(y_A-y_B)^2} \]

我们不妨将等式的意义看作：

\[A(x,y)到B(a,b)的距离=\sqrt c \]

根据圆的集合定义（平面内到一个定点距离为定长的点的集合是圆），所有满足这个等式的点\(P(x, y)\)都在以\((a,b)\)为圆心，\(\sqrt c\)为半径的圆上，这个表达式也就表示这个唯一的圆。

稍稍改变一下，我们得到了圆的方程：

在平面直角坐标系\(xOy\)中，以\(a,b\)为圆心，\(r\)为半径的圆的方程可以表示为：

\[\bold{(x-a)^2+(y-b)^2=r^2} \]

其中，\(a,b,r\)为常数，\(r>0\)。

在一个平面内，如果你知道了圆心的坐标和半径，在几何上，你可以通过一把圆规确定唯一圆；在代数上，你可以写出唯一的圆方程。例如，圆心为\((3,-4)\)，半径为\(5\)的圆方程为：

\[(x-3)^2+(y+4)^2=25 \]

由于将\(x=0, y=0\)代入，等式成立，因而\((0,0)\)在这个圆上。

材料阅读：点与圆的位置关系

已知平面内一点\(P(x,y)\)，和一个\(\odot O:(x-a)^2+(y-b)^2=r^2\)，则：

\(P\)在圆内 \(⇔\) \(OP<r\) \(⇔\) \((x-a)^2+(y-b)^2<r^2\)；

\(P\)在圆上 \(⇔\) \(OP=r\) \(⇔\) \((x-a)^2+(y-b)^2=r^2\)；

\(P\)在圆外 \(⇔\) \(OP<r\) \(⇔\) \((x-a)^2+(y-b)^2>r^2\)；

1.2 “圆元素”在坐标系中的表示

所谓“圆元素“，实际上是指和圆有一定关联，也就是本章所学的概念和模型，如 半径、直径、弦、弧、圆心角、圆周角、内接多边形、外切多边形、切线 等。在几何中你可以很直观地看出它们之间的关联，但是如果换到代数里，可能需要一些小小的计算了。

半径、直径和弦

按照正常的直线方程计算即可，其中对于半径和直径，应该把圆心\((a,b)\)代入方程求解。至于和圆的交点，将会在下一节详细讲解。

* 圆心角和圆周角

我们可以推广一下，实际上，我们需要计算坐标系中任意两条直线的夹角大小。

本部分需要一定三角函数的知识储备。

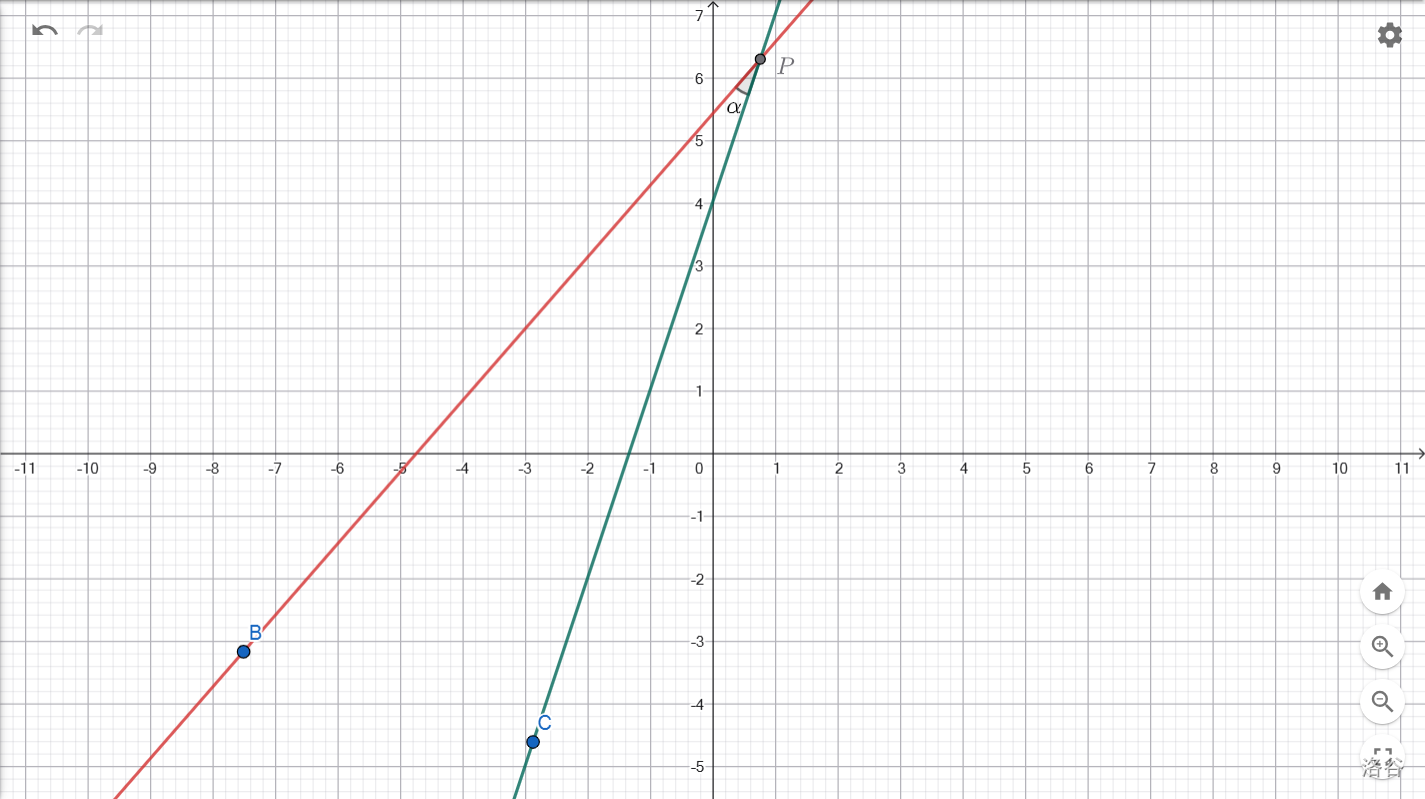
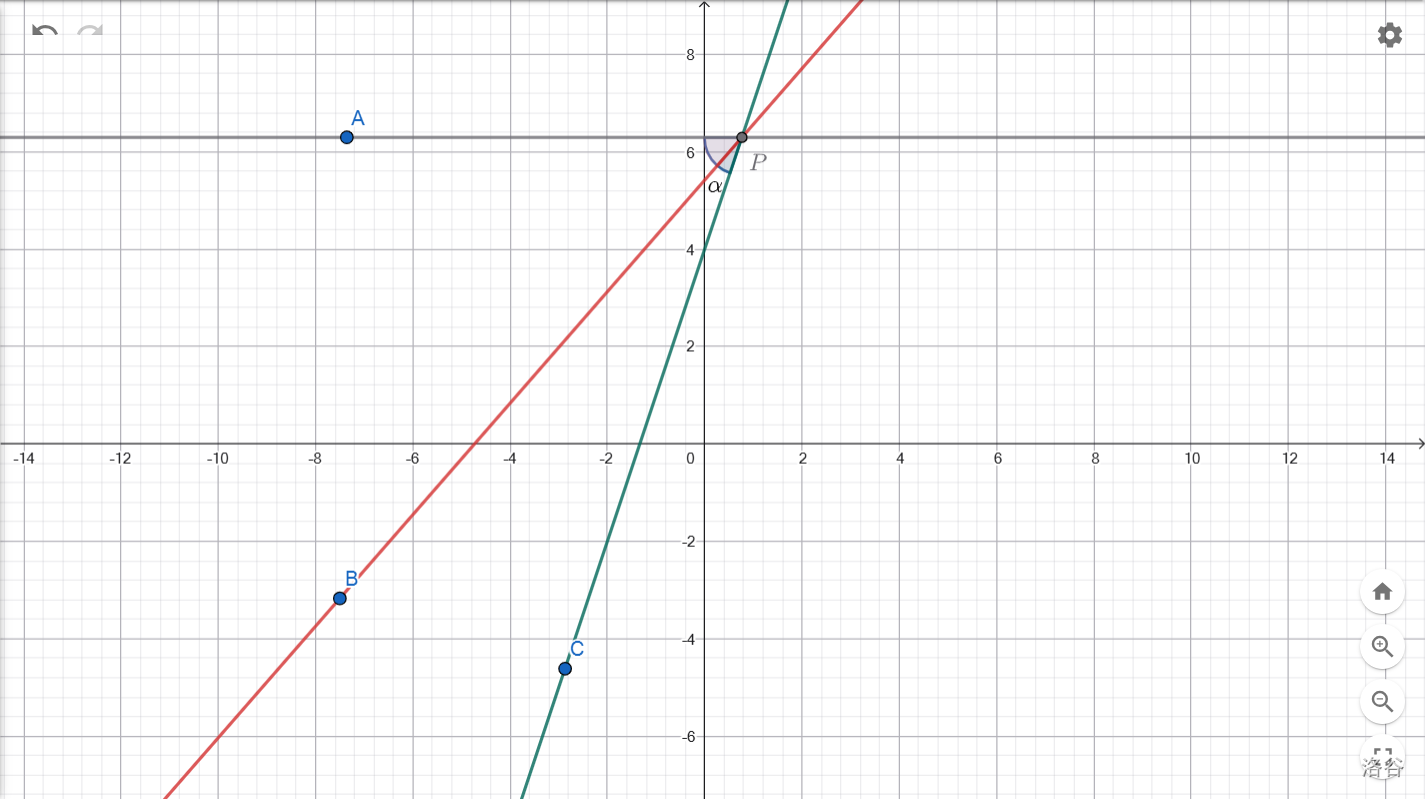
注意看，这里有两条直线，\(y=k_1x+b_1\)和\(y=k_2x+b_2\)。如何求它们的夹角\(\alpha\)的大小呢？

考虑到普遍性的要求，我们把夹角统一转化到水平方向上去。

从图上看，即要求\(\angle APC-\angle APB\)。幸好我们学过坡度和坡角的关系，即\(\tan \alpha=\frac h l\)；又由于直线的点斜式计算方法是\(k=\frac {\Delta y} {\Delta x}=\frac h l\)，所以，斜率\(k\)其实已经可以代替\(\frac h l\)存在。因此，坡角\(\alpha\)必定满足\(\tan \alpha=k\)；如果你还知道一点"反三角函数"，那就更好了，\(\alpha\)可以表示为\(\alpha=\arctan k\)。但\(k\)有正负，为了保证\(k\)的数值不超出初中数学的纲，我们步步取绝对值。得到如下计算公式：

\[\bold{\alpha=|\arctan |k_1|-\arctan |k_2||} \]

这就是夹角的计算公式。

切线

问题

在平面直角坐标系\(xOy\)中，存在一个圆\(x^2+y^2=r^2(r>0)\)。求过圆上一点\((m, n)\)的切线\(l_t\)的表达式。

观察发现，这个圆的圆心就是坐标原点，可谓是帮我们省去了许多麻烦。应该考虑如下思路：

要求切线，孤零零一个切线摆在那儿，显然是没法求的。目前只知道一个条件，切线过\((m,n)\)，其余尚且未知。

一个点当然无法确定一条直线，因此再观察，发现有切线的条件，联想切线的性质。做几何时，遇到切线通常都要连半径，那这边我也连个半径试试看。毕竟切线性质很少，最常用的就是垂直于半径了吧！

既然垂直于半径，首先要把半径表示出来。之前说半径按照正常的直线方程求解，现在已知半径过\((0,0)\)和\((m,n)\)，完全能算。算得：

\[r:y=\frac n mx \]

如何表示垂直？非常明了，运用推论\(k_1\cdot k_2=-1\)可解。\(l_t⊥r\)，因此有：

\[k_{l_t}\cdot k_r=-1 \]

代入\(k_r=\frac n m\)，有：

\[k_{l_t}=\frac {-1} {\frac n m}=-\frac m n \]

现在切线斜率已知，还知道过\((m,n)\)，就可以求出切线表达式。设切线表达式\(y=-\frac m nx+b\)，代入\((m,n)\)，有：

\[-\frac m n\cdot m+b=n \]

整理，得：

\[b=n+\frac {m^2} n=\frac {m^2+n^2} n \]

Link：第三章 快速计算与绘图——点斜式。

最终求得：

\[\bold{l_t:y=-\frac m nx+\frac {m^2+n^2} n} \]

到了高中学习直线方程时，不一定要把\(y\)单独写在等式的一边，那么这个式子可以写成更优美的形式：

\[\bold{l_t:mx+ny=m^2+n^2} \]

这就是圆上一点的切线方程，其中圆心和坐标原点重合。