二次函数的深层理解、题目技巧和应用
请在学习完初识二次函数后再来学习。
观前提示:本章会不定期增补修改。
对\(a,b,c\)的理解
前面已经说过,\(a\)决定的是开口方向和大小。
那\(b\)呢?
根据顶点\(V\)的横坐标\(-\frac b {2a}\)可知,如果\(a,b\)异号,则顶点横坐标为正;同号则为负。
你可能认为这没有什么用,但请务必记住。在后面的题目中,你会见识到这一点的重要性。
\(c\)就比较简单了,其表示的是抛物线与\(y\)轴交点的纵坐标(进阶一点来说就是在\(y\)轴上的截距)。
待定系数法确定二次函数
主播主播你怎么只知道抄你的反比例函数
别问,问就是懒得重想标题了
来看一道期末真题。
(\(2023\)·鼓楼)求下列二次函数的表达式:
\((1)\)已知二次函数图像经过点\((3,0)\),\((-2,0)\)和\((0,6)\)。
\((2)\)已知二次函数图像顶点为\((2,0)\)且经过\((-2, 4)\)。
第一题还是比较简单的,照着一次函数和反比例函数来:
解:设二次函数表达式为\(y=ax^2+bx+c(a\neq 0)\)。
由题意得:
\[\left\{ \begin{aligned} &9a+3b+c=0 \\ &4a-2b+c=0\\ &c=6\\ \end{aligned} \right. \]爆破一手,解得:
\[\left\{ \begin{aligned} &a=-1 \\ &b=1\\ &c=6\\ \end{aligned} \right. \]\[\therefore 二次函数表达式为y=-x^2+x+6 \]
第二题,我先把笨办法讲掉,然后再说简单的。
解:设二次函数表达式为\(y=ax^2+bx+c(a\neq 0)\)。
由题意得:
\[\left\{ \begin{aligned} &-\frac b {2a}=2 &①\\ &\frac {4ac-b^2} {4a}=0&②\\ &4a-2b+c=4&③\\ \end{aligned} \right. \]有些同学不知道怎么解的,我把简易过程放在这里。
\[②, 4a\ne 0\Rightarrow 4ac-b^2=0\Rightarrow b^2=4ac \]\[①\Rightarrow b=-4a \]\[把b=-4a代入②\Rightarrow 16a^2=4ac \]\[\because a\ne 0\therefore c=4a \]\[把b=-4a, c=4a代入③\Rightarrow a=\frac 1 4 \]经过代数爆破,非非非非非非常容易解得:
\[\left\{ \begin{aligned} &a=\frac 1 4 \\ &b=-1\\ &c=1\\ \end{aligned} \right. \]\[\textcolor{red} {经检验},二次函数表达式为y=\frac 1 4x^2-x+1 \]
想必各位已经想到第二种方法了,那就是用顶点式。
解:设二次函数表达式为\(y=a(x+h)^2+k(a\neq 0)\)。
\[\because 顶点坐标为(2, 0) \]\[\therefore h=-2, k=0\Rightarrow y=a(x-2)^2 \]由题意得:
\[a(-2-2)^2=4 \]解得:
\[a=\frac 1 4 \]\[\therefore 二次函数表达式为y=\frac 1 4(x-2)^2 \]
你必须承认这是本题最简单的方法了。只要一个一元一次方程,岂不美哉!
你又动起了脑筋。哎,顶点式这么好用,那\((1)\)能不能用啊。
当然可以。
解:设二次函数表达式为\(y=a(x+h)^2+k(a\neq 0)\)。
\[\because 函数图像过(3, 0), (-2,0) \]\[\therefore 根据对称性,顶点横坐标为\frac {3+(-2)} 2=\frac 1 2 \]\[\therefore h=-\frac 1 2\Rightarrow y=a(x-\frac 1 2)^2+k \]由题意得:
\[\left\{ \begin{aligned} &a(3-\frac 1 2)^2+k=0 \\ &a(-\frac 1 2)^2+k=6\\ \end{aligned} \right. \](要注意这边千万不能再用\((3,0)\)和\((-2, 0)\)了,不然算出来方程组无解的。)
解得:
\[\left\{ \begin {aligned} & a=-1\\ & k=\frac {25} 4\\ \end {aligned} \right. \]\[\therefore 二次函数表达式为y=-(x-\frac 1 2)^2+\frac {25} 4 \]
你必须承认这是本题最简单的方法了。只要一个二元一次方程组,岂不美哉!
不!这不是最简单的方法!
我 们 要 设 表 达 式 为 \(y=a(x-3)(x+2)(a\ne 0)\) 。
由 题 意 得
\[-3\cdot 2a=6 \]解 得
\[a=-1 \]\[\therefore y=-(x-3)(x+2)=-x^2+x+6 \]
为什么能这么设?这是我们要考虑的一个问题。以下内容仅做拓展。
都说三点确定一条抛物线(第\((1)\)题的法\(1\)已经告诉我们),那如果一条抛物线与\(x\)轴有两个交点,那就是已经确定了抛物线的零点位置。
根据十字相乘法,能够因式分解的二次三项式\(x^2+px+q\),总能分解为\((x+a)(x+b)\)的形式。那为何不直接将二次函数中的二次三项式写成十字相乘的形式呢?
需要说明一点,即我们这里的十字相乘不再局限于整数域(\(\N\)),而扩展到了有理数域。也就是说,分解后的结果可以是\((x-1145.4514)(x+5418.4188)\),而“能因式分解”的条件也变为了:二次三项式等于\(0\)所形成的方程有两个不等的实数根。
目的是因式分解;条件是与\(x\)轴有两个交点,或者说能够因式分解。步骤就很简单了。因式分解后,二次三项式变为一个多项式乘积的形式。只要任意一个因式为\(0\),最终值一定为\(0\)。
令二次三项式为\(S\)。根据试根法,因为当\(x=3\)时\(S=0\),因此\(S\)中必含因式\(x-3\);同理,\(S\)中必含因式\(x+2\)。由于它是二次三项式,不可能有其它含\(x\)的因式,故因式分解后的基本形式确定:\((x+2)(x-3)\)。
当你确定基本形式后,你会发现如果直接将该形式作为二次函数的运算部分,二次项系数就被固定下来是\(1\)了。况且,你这才两个点呢。要想控制二次项系数(或者,从下面的图中看来,控制开口大小和方向),就加上一个系数\(a\)。
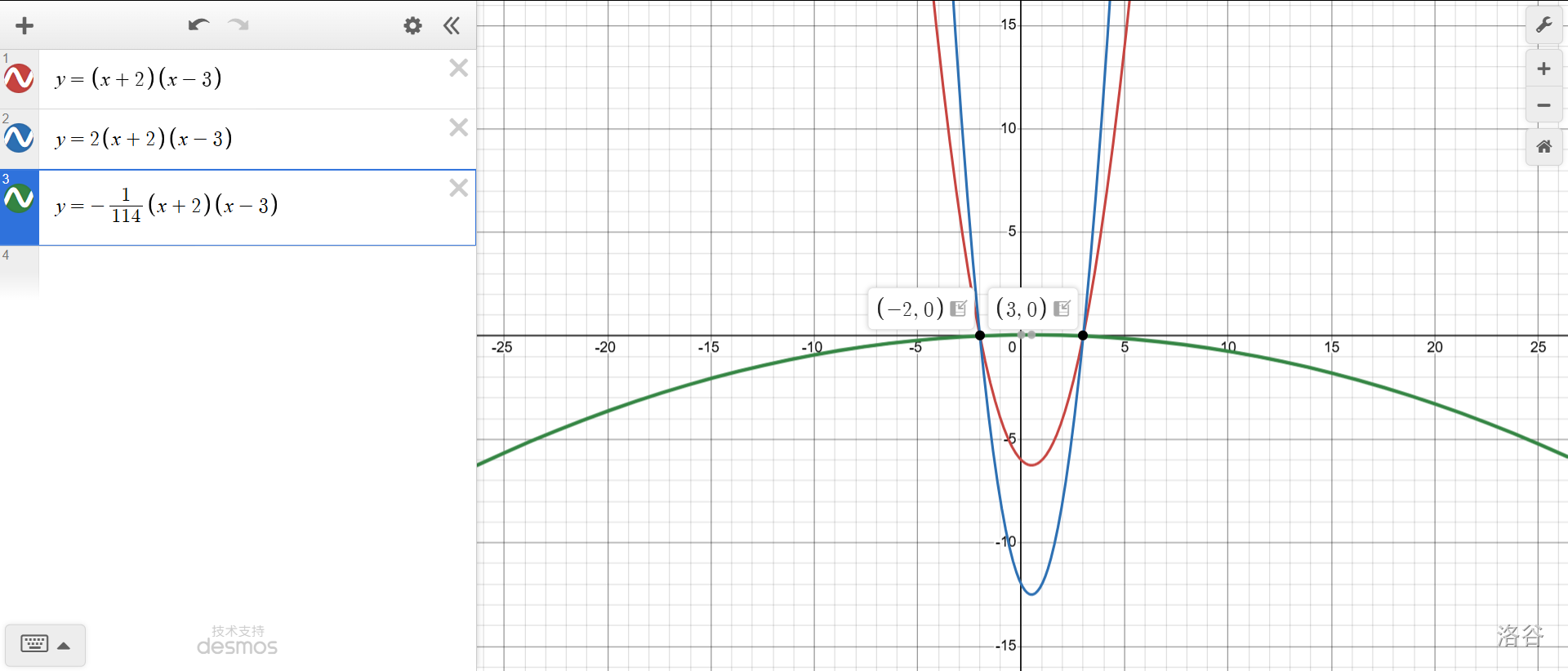
拓展部分到此结束。如果上面没听懂,你只需要记住:
如果已经给出一个二次函数和\(x\)轴有两个交点,最好是给出其中一个或两个交点的坐标(设它们分别为\((p, 0)\),\((q, 0)\)),就可以使用一种课本不承认的表示形式:\(y=a(x-p)(x-q)\)。这样通常可以简便计算。
这禁忌之术就被称为:
交点式(\(\text {intersection form}\))。
二次函数与取值范围(基础篇)
对于抛物线\(y=x^2\),当\(-2<x\le-1\)时,\(y\)的取值范围是多少?
简单!当\(x=-2\)时\(y=4\);当\(x=-1\)时\(y=1\)。取个中间,注意等号,搞定!
好!好啊。那改下题目,看阁下如何应对!
对于抛物线\(y=-2x^2\),当\(-3<x<1\)时,\(y\)的取值范围是多少?
当\(x=-3\)时\(y=-18\);当\(x=1\)时\(y=-2\)。取个中间,注意等号,搞定!
住口!你且看看图像,是如你所言么?
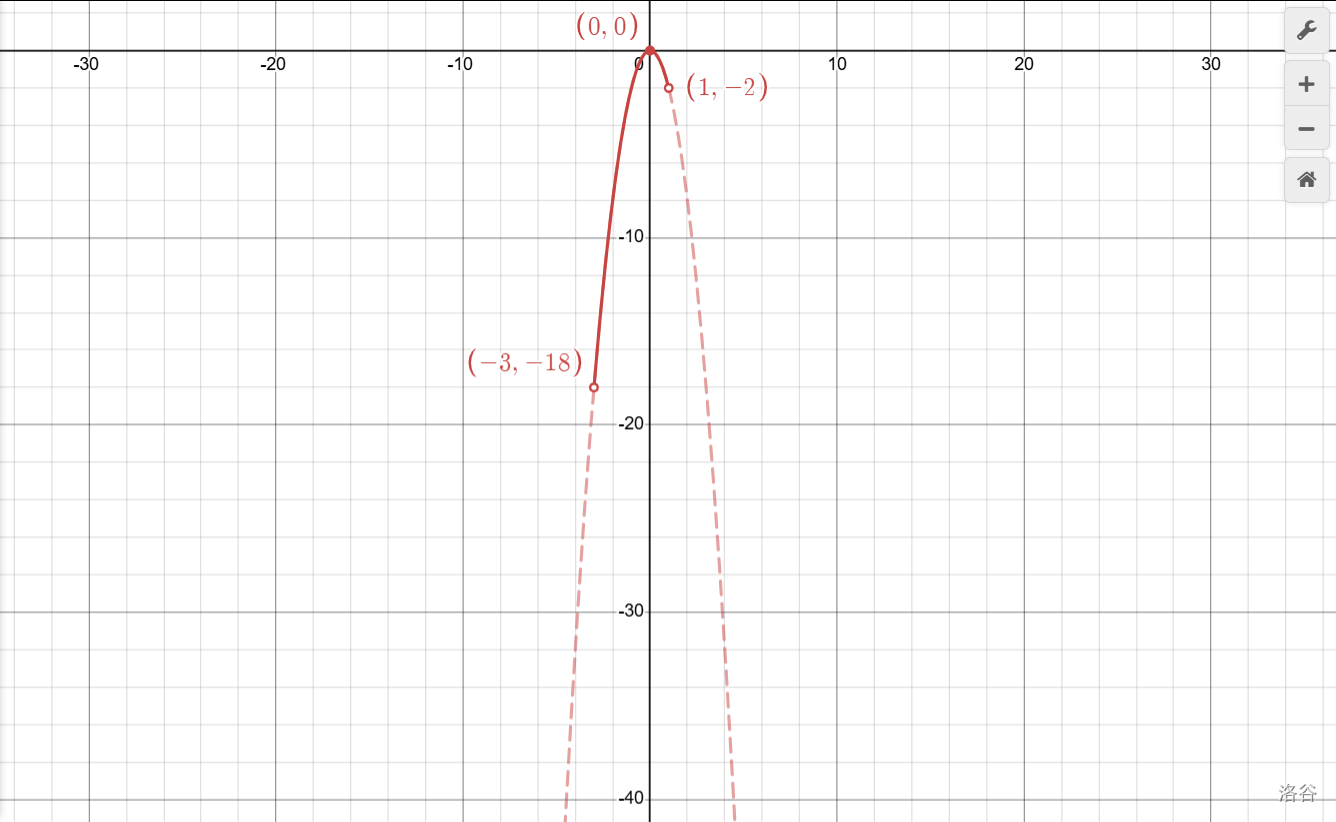
原来,因为二次函数有多个增减性,在顶点处会拐弯,因此要分段考察。做这类题时,应遵循如下步骤:
- 看到函数,先求顶点坐标。
\(y=-2x^2\),显然顶点坐标\((0,0)\)。
- 看取值范围是否跨越了顶点。
- 如果没跨越,按照许韦升的方法算即可。
- 如果跨越了,从顶点处劈两半分别计算,然后求他们整体覆盖的取值范围。
分成\(-3<x\le 0\)和\(0<x<1\)计算。
它们都没有跨越顶点,因此照常计算,一个算得\(-18<x\le 0\),一个算得\(-2<x< 0\)。
它们两个合并起来,就是\(-18<x\le 0\)。
当然,最保险的方法还是画图。主播当年错过这道题,原因就是没画图,然后\(0\)没取到。
对于下面这一类题目,那还是推荐保险一点的方法。
对于抛物线\(y=-2x^2\),当\(-3<y\le -1\)时,\(x\)的取值范围是多少?
放心吧,你脑子是转不过来的,老老实实画图!
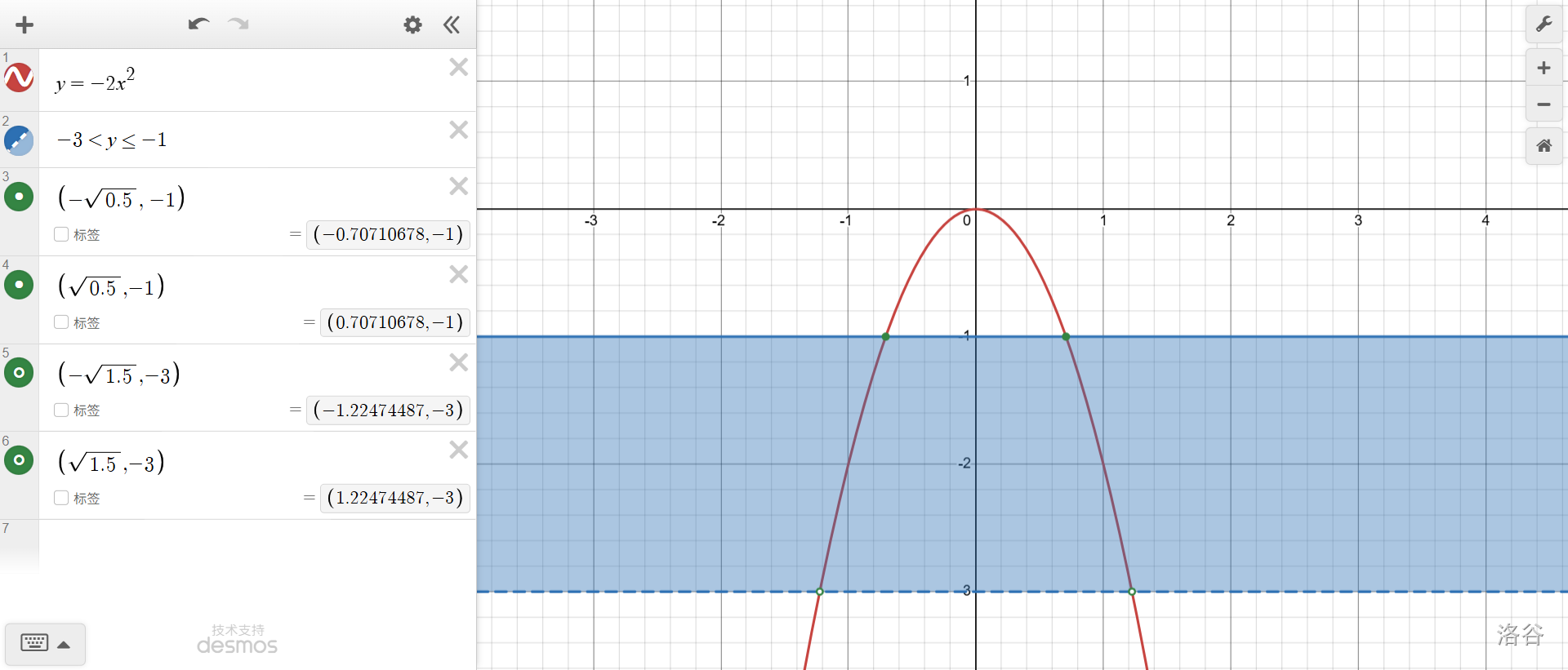
就看被蓝色区域覆盖的函数图像,竟然还是个分段函数。\(y=-3\)是虚线,\(y=-1\)是实线,这个一定要标好。四个交点简单算下:
立马得到答案\(-\frac {\sqrt 6} 2<x\le -\frac {\sqrt 2} 2\)或\(\frac {\sqrt 2} 2\le x<\frac {\sqrt 6} 2\)。
这类题目主要就是细心,不能少等号,或者没取到顶点。想验算?那就画图!这种分是不能失的。
画图技巧
为什么单独劈一块讲“画图技巧”呢?
画一次函数很简单,取两个点(一般是与\(x, y\)轴的交点),尺子一连。
画反比例函数也不难,取几个点(一般是\(k\)的因数为横纵坐标)大致一连,反正双曲线长得都差不多。
那抛物线呢?既有开口方向、开口大小的限制,还要确定位置,想画的相对准还是比较难的。
对策就是我们之前顺嘴提过的一点。

那么如何快速计算顶点呢?
我们都知道顶点坐标\((-\frac b {2a}, \frac {4ac-b^2} {4a})\),但是真的要把\(a,b,c\)代进去挨个算吗?我们体验一下,假设要计算\(y=-x^2+2x+3\)的顶点坐标。
嗯,先提\(a,b,c\)。
\[a=-1, b=2, c=3 \]算横坐标。
\[-\frac b {2a}=-\frac 2 {2\times (-1)}=-\frac 2 {-2}=1 \]算纵坐标。
\[\frac {4ac-b^2} {4a}=\frac {4\times (-1)\times 3-2^2} {4\times (-1)}=\frac {-16} {-4}=4 \]哦!顶点坐标是\((1, 4)\)。
不仅费草稿纸,又费脑子,还容易错。看到那么长一个分式,你还想算吗?因此接下来给一个快速算顶点的方法。
第一步还是先提\(a,b,c\)。
\[a=-1, b=2, c=3 \]观察到\(a,b\)异号,反过来横坐标为正。
符号不用管了,直接数值除以两倍数值,\(2\)除以\(2\)倍\(1\),顶点横坐标是\(+1\)。下一步算纵坐标。\(2B\)才把\(\frac {4ac-b^2} {4a}\)代入呢!我直接
\[当x=1时,y=-1^2+2+3=4 \]哦!顶点坐标是\((1,4)\)。
确定顶点后,先点出来,大致位置即确定。
然后看\(a=-1\),说明开口朝下,大小和\(y=x^2\)一样,就可以动笔了。
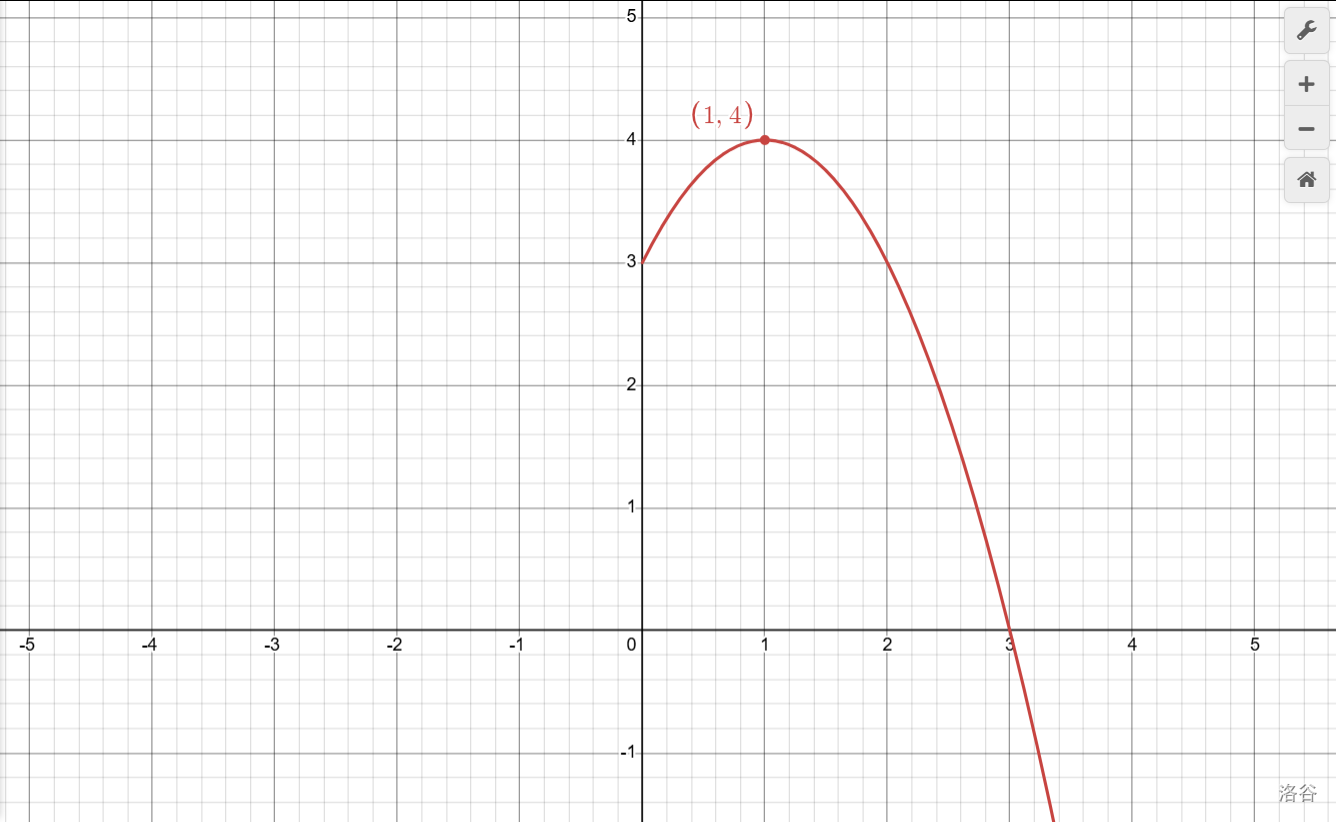
最后可以再看一点,就是和\(y\)轴的交点为\((0,3)\)。抛物线往上怼,然后一路降下去。
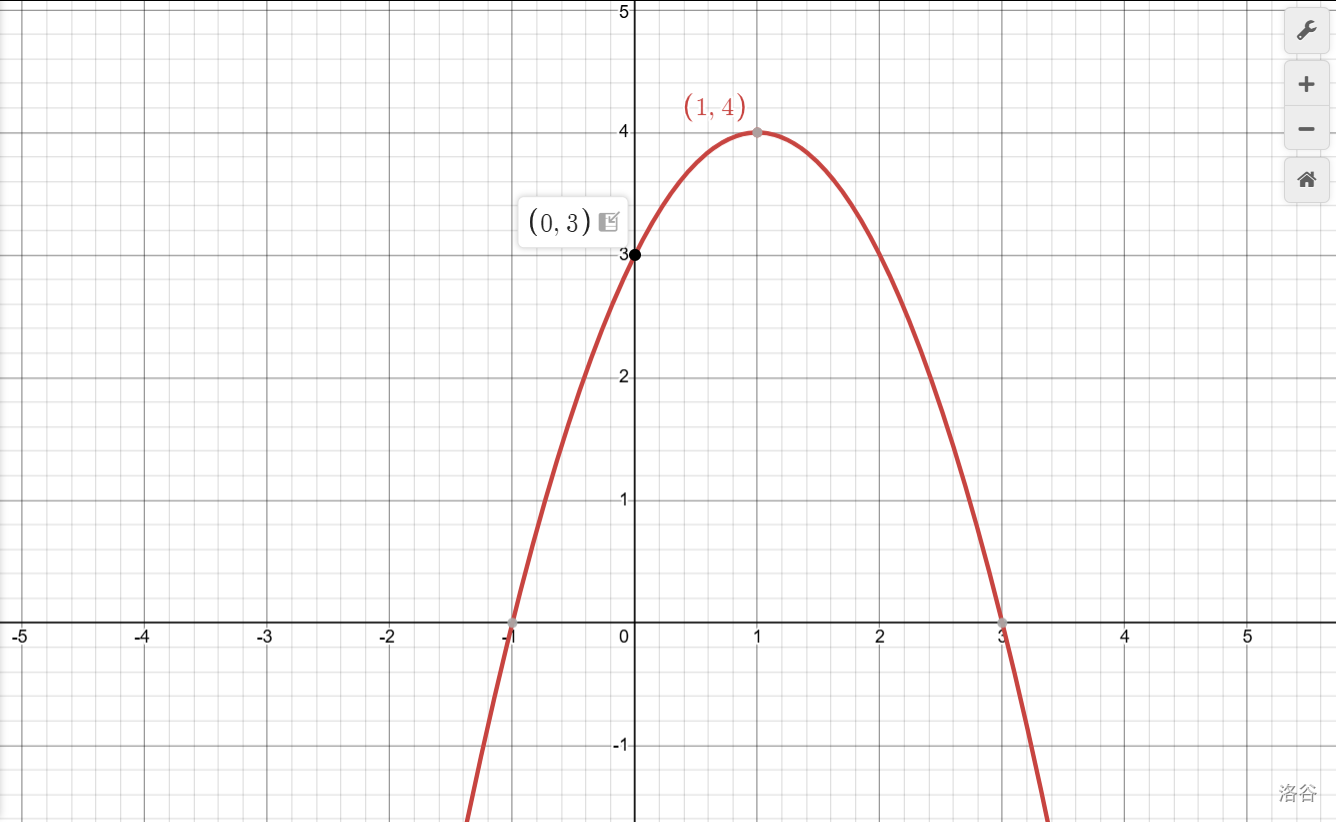
这样画出的图像大致准了,研究问题时就不会遇到精确度上的问题。
二次函数与取值范围(提高篇)
阅读下面的材料。
小明在学习中遇到这样一个问题:求二次函数\(y=x^2-6x+7(1\le x\le m)\)的最大值。他画图研究后发现,\(x=1\)和\(x=5\)时的函数值相等,于是他认为需要对\(m\)分类讨论。
他的解答过程如下:
\[\because y=x^2-6x+7的对称轴为直线x=3 \]\[\therefore x=1和x=5时的函数值相等 \]\[若1\le m< 5,则x=1时,y_{max}=2 \]\[若m\ge 5,则x=m时,y_{max}=m^2-6m+7 \]请你参考小明的思路,解答下列问题:
\((1)y=2x^2+4x+1(-2\le x\le 4)\)的最大值为\(\_\_\_\)。
\((2)\)求\(y=2x^2+4x+1(p\le x\le 2)\)的最大值。
\((3)\)若\(y=2x^2+4x+1(t\le x\le t+2)\)的最大值为\(31\),则\(t\)的值为\(\_\_\_\)。
在下面的文字中,我先从高中借一点符号,规定\(f(a)\)表示\(x=a\)时的函数值。其实就是因为不想写那么多字了。
第\((1)\)题很简单,代入基础篇的技巧即可。
\((2)\)题你一看,跟小明的例题没有区别。那我们就先仿它一手,接下来再慢慢讲原理。
解:$$\because y=2x^2+4x+1的对称轴为直线x=-1$$
\[\therefore x=2和x=-4时的函数值相等 \]\[若-4< p\le 2,则x=2时,y_{max}=17 \]\[若m\le -4,则x=p时,y_{max}=2p^2+4p+1 \]
看来光模仿还模仿不来,像这些\(p\)的取值范围,不搞懂是根本改不过来的。话不多说,先画图。
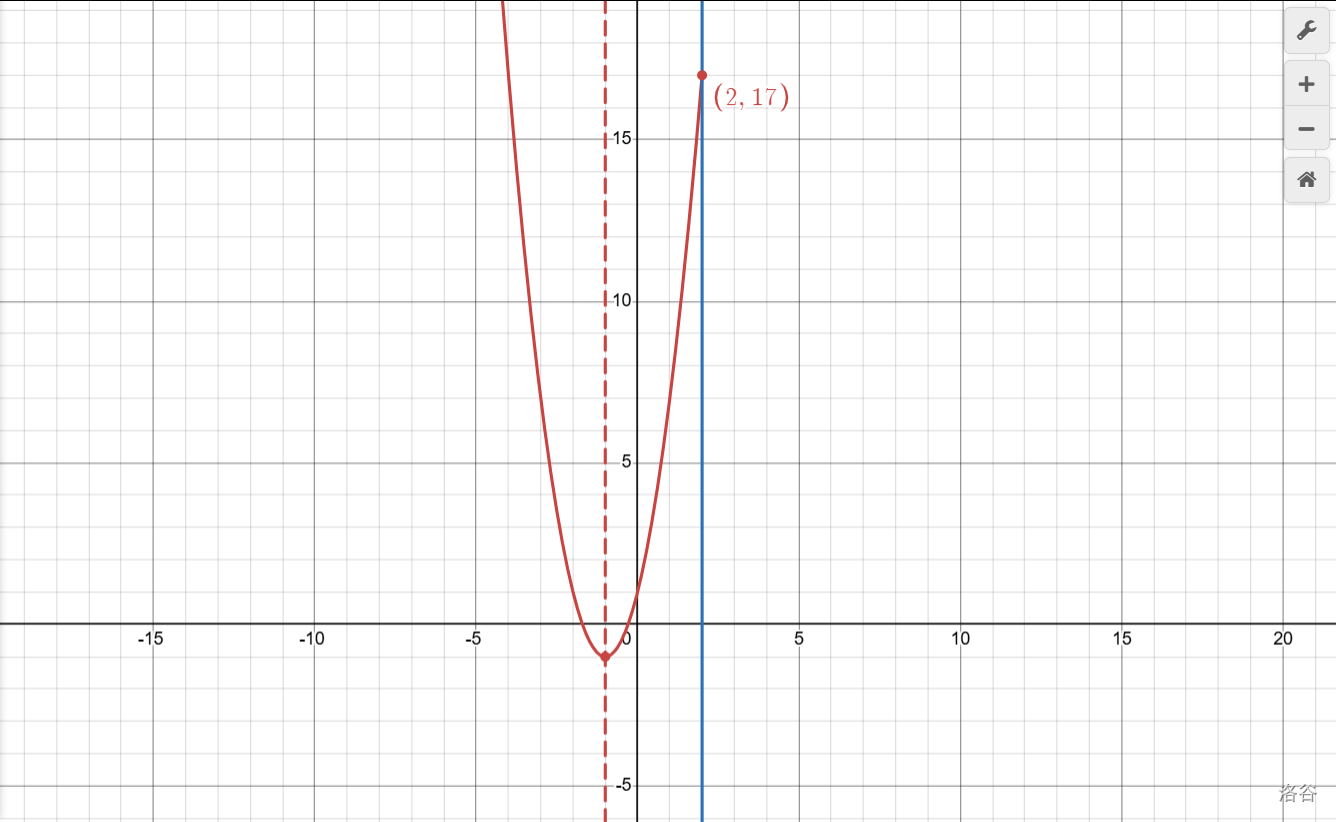
首先可以肯定的是,通过\(p\le x\le 2\)可以看出\(p\le 2\)。那我们就把\(p\)从\(2\)开始,往小的移动,看取值范围怎么变化。
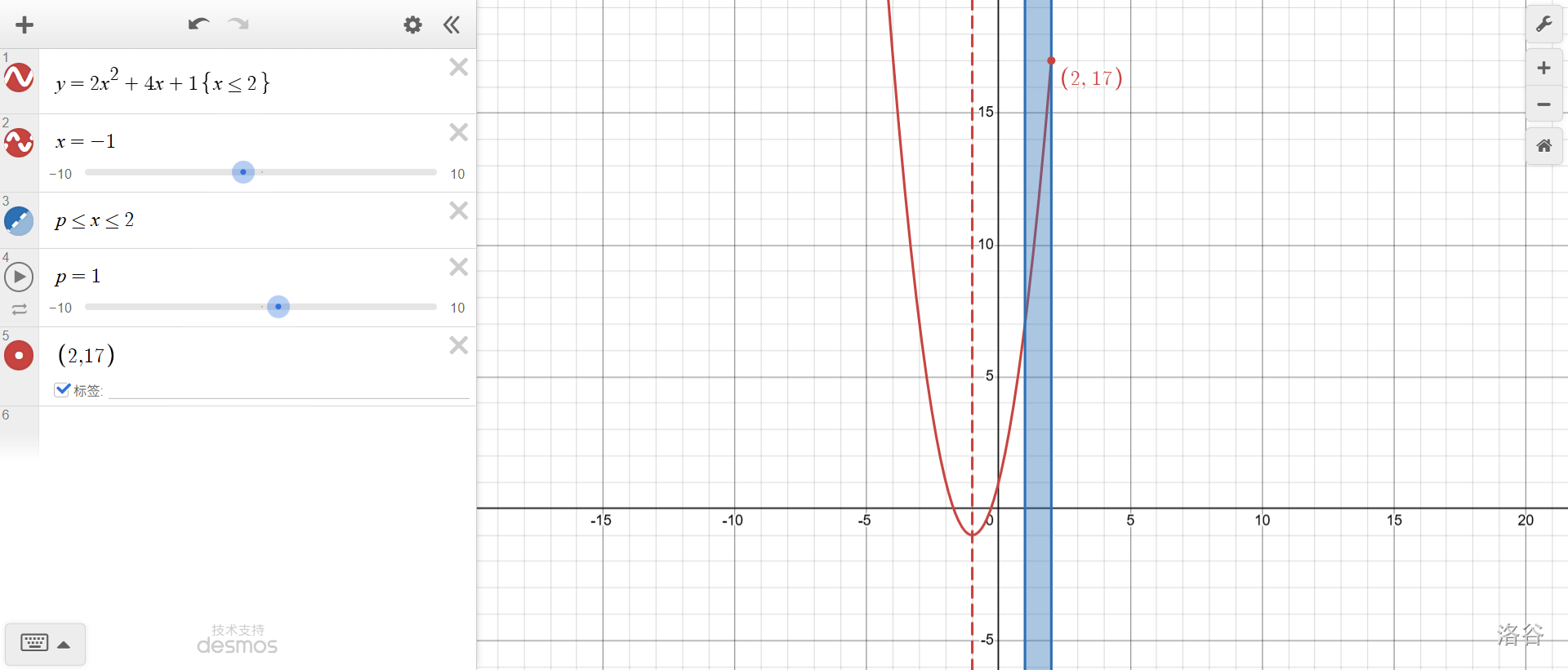
上面是\(p=1\)时。仔细看蓝色区域里的图像,单调递增,因此最大值是\(x=2\)时的函数值,即\(f(2)\)。
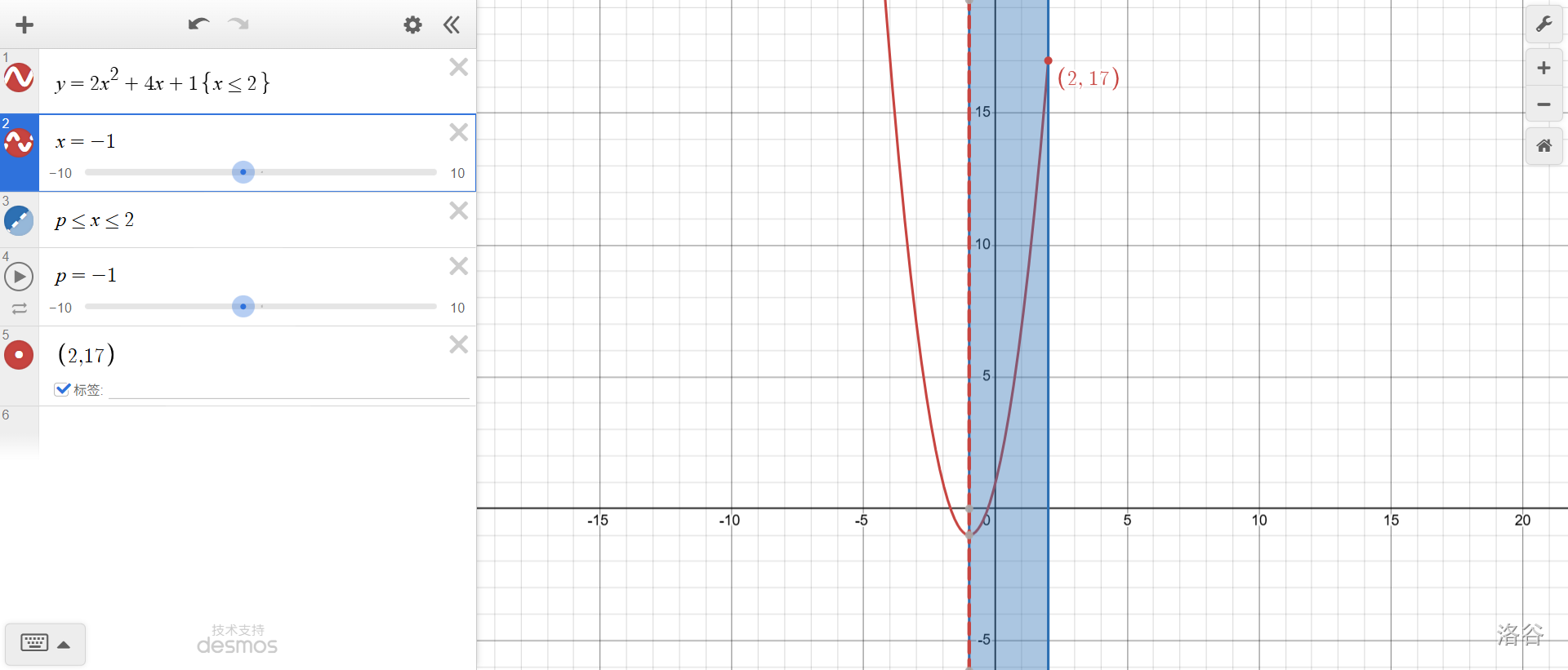
\(p=-1\)了,最大值还是\(f(2)\)。
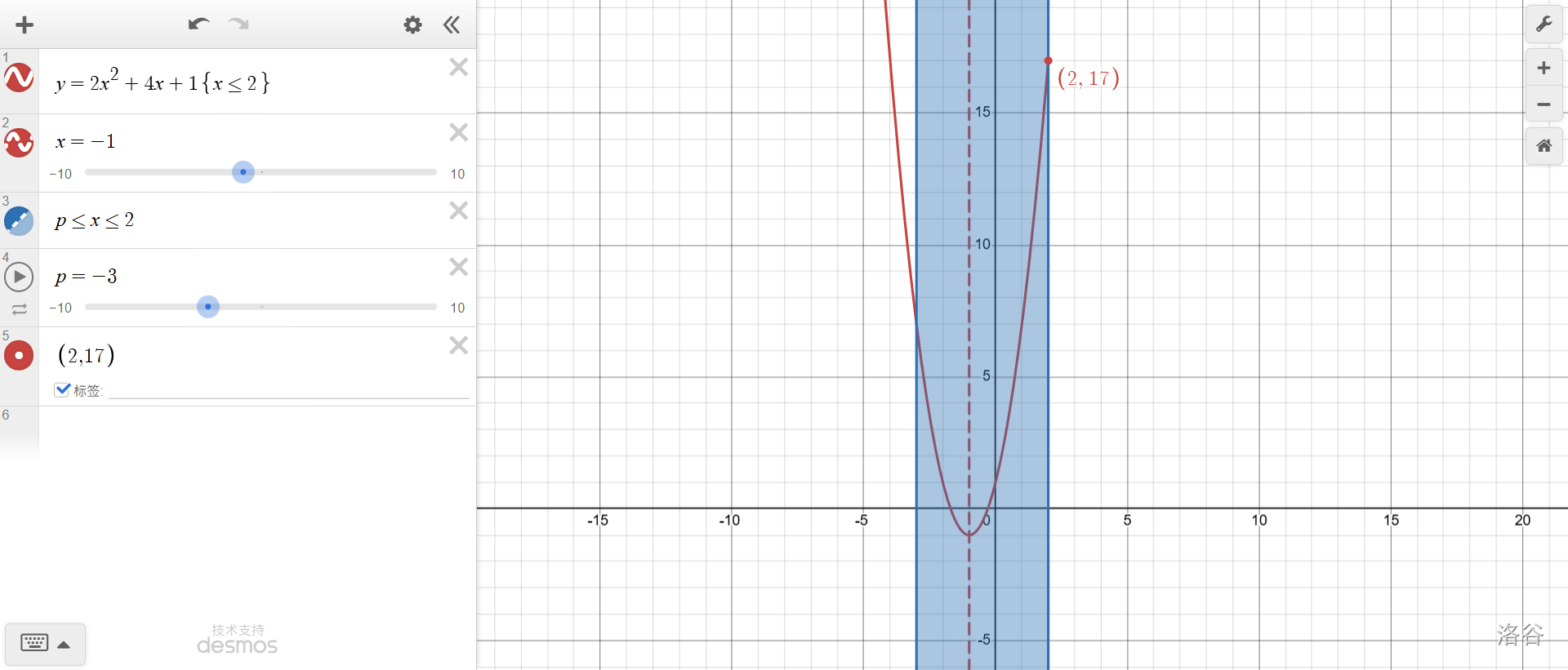
\(p=-3\),已经跨越了顶点,于是劈成两半。左半边最大值\(f(-3)\),右半边最大值\(f(2)\)。\(f(2)>f(-3)\),所以最大值依旧是\(f(2)\)。
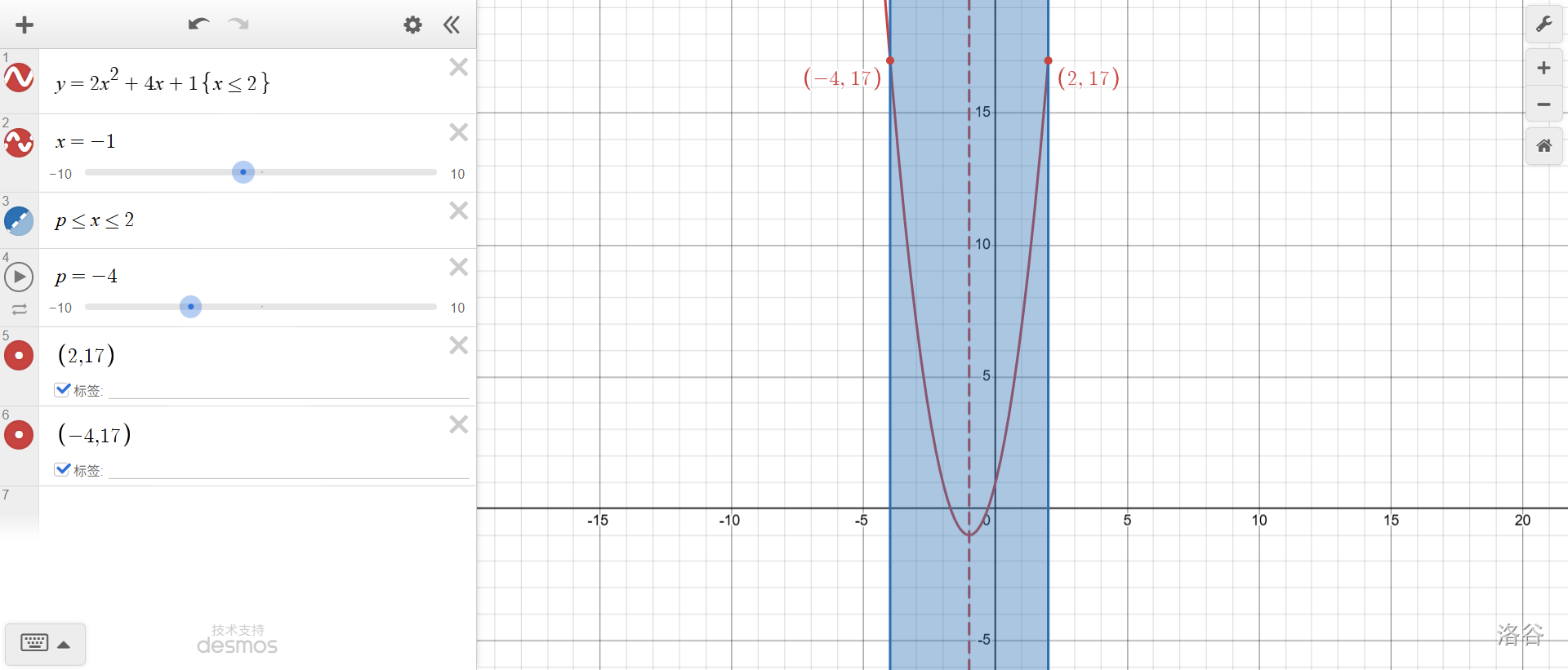
\(p=-4\)时,\(f(2)=f(-4)\),这也是题目中把该点作为转折点的原因。这一点以后,\(f(2)<f(p)\)了,因此最大值变成\(f(p)\),并且一直继续下去(这是由于\(x<-1\)时,\(y\)随\(x\)的减小而增大,对于\(p<-4\),\(f(p)>f(-4)=f(2)\))。
懂得这种“拖进度条式”的分析方法后,第\((3)\)题也可以秒解了。\(t\le x\le t+2\),翻译一下就是宽度为\(2\)的“进度条”在函数上来回拖动,在某个时候,条内函数的最大值是\(31\),求这个时候进度条拖到哪儿了。
那我们就拽拽看!
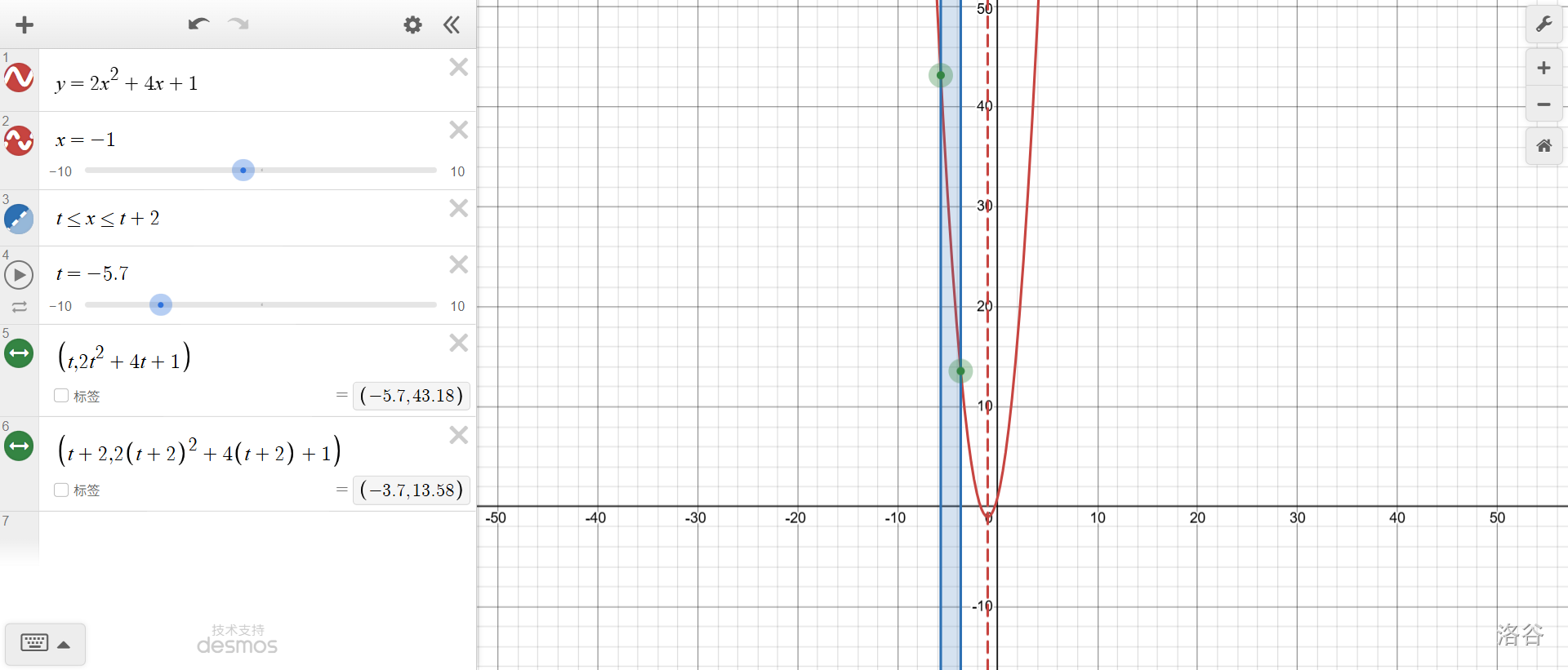
先从\(t+2\le-1\)(进度条全部在对称轴左侧)开始。此时,容易看出,最大值为\(f(t)\)。
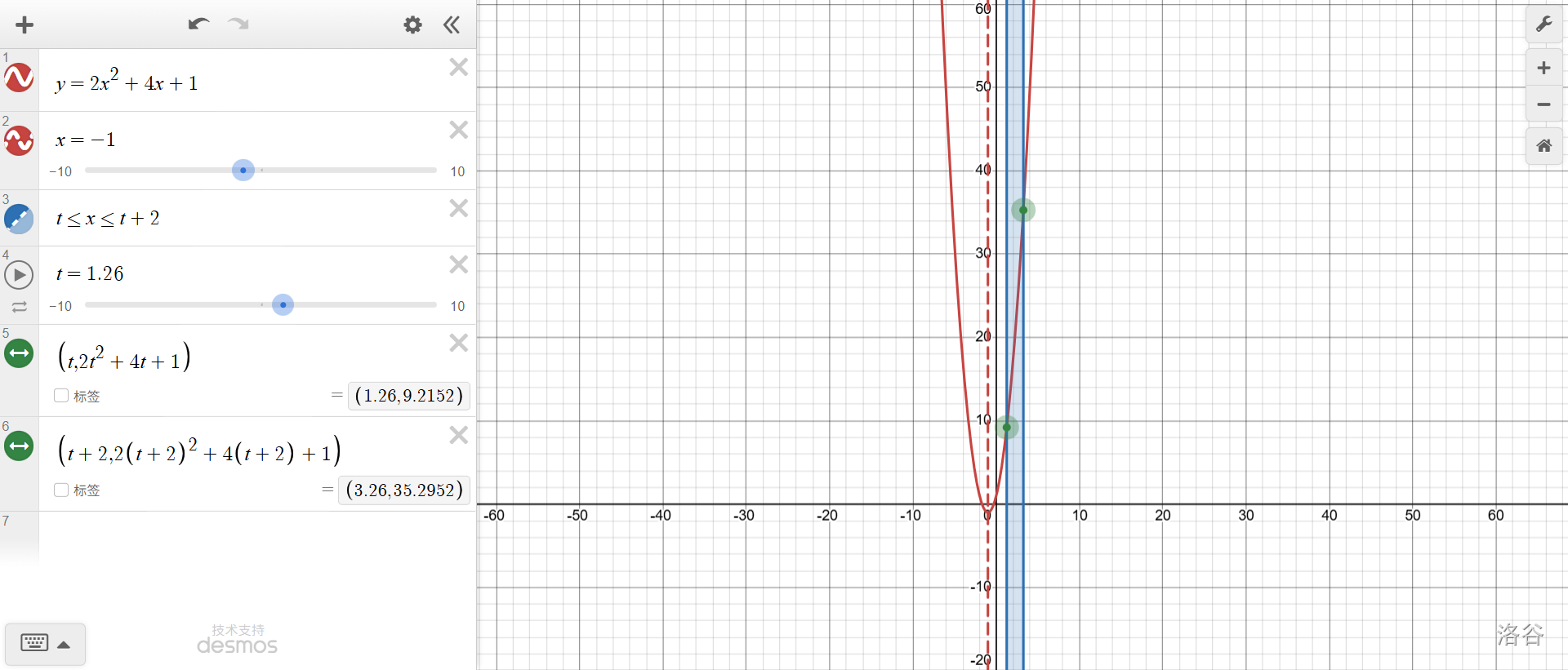
对称着说,当\(t\ge -1\)(全部在对称轴右侧)时,最大值为\(f(t+2)\)。
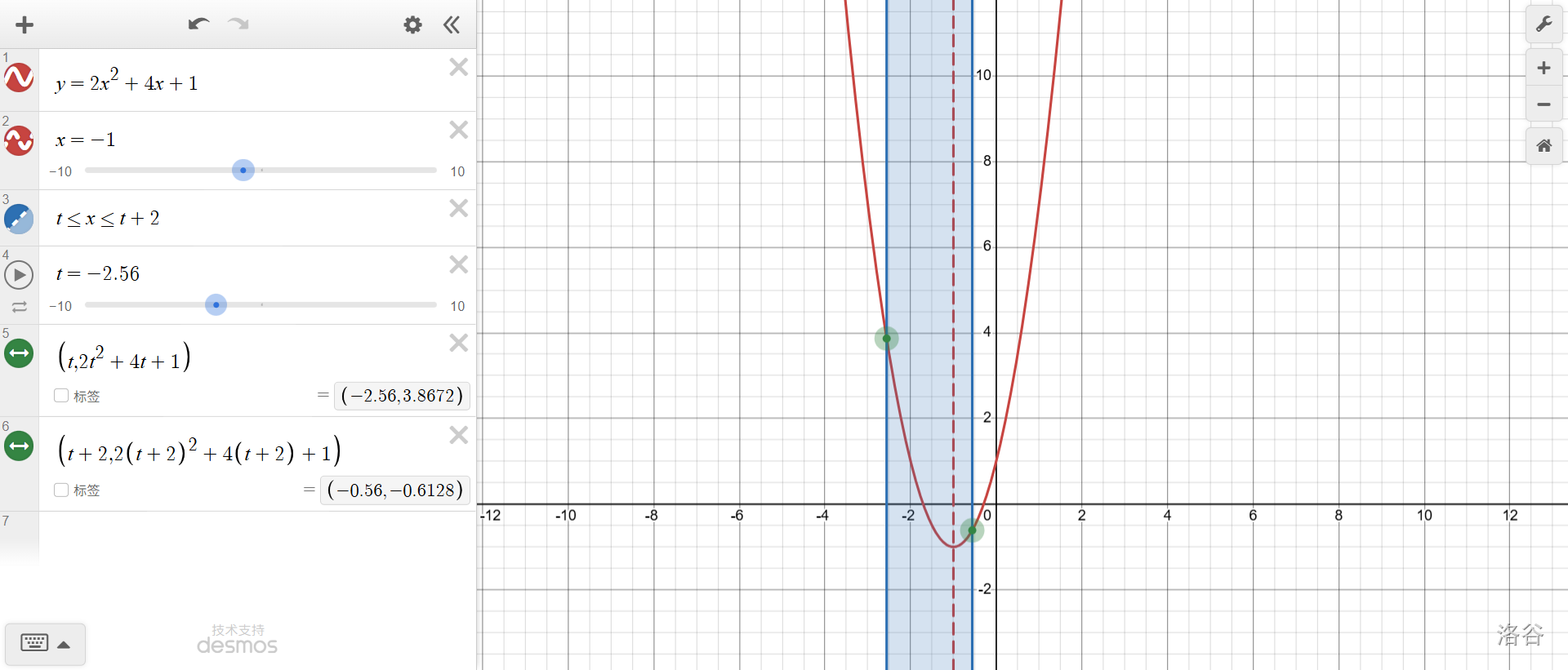
接下来是跨越对称轴的一部分。上面展示的情况下,\(y_{max}=f(t)\),但并非总是如此。对称轴两侧增减性不同,随着进度条向右拖动(\(x↑\)),一侧下降,一侧上升。由此推断必定有一个转折点,满足通过该点之后,\(f(t+2)>f(t)\),从而最大值变为\(f(t+2)\)。
再联系对称性,可以知道,转折点(即\(f(t)=f(t+2)\)时)肯定是对称轴处于\(t\)和\(t+2\)正中间,即\(t+1=-1, t=-2\)的时候。
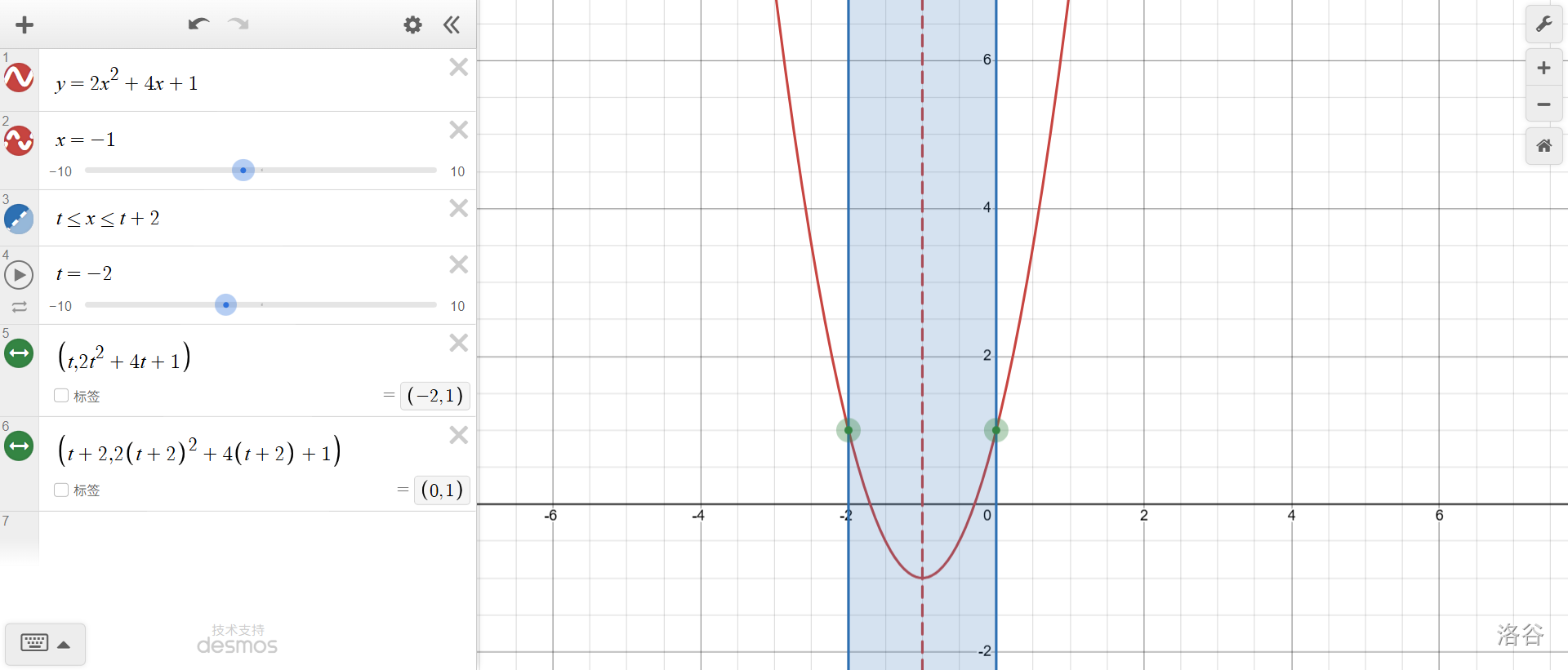
不知道你有没有发现,\(y_{max}\)和\(t\)之间,其实也是一种函数关系!根据我们发现的结论,表达式如下:
还是分段函数。整理得:
我们要求\(y_{max}=31\)时\(t\)的值。现在目标明确,接下来不用多说了吧。
当\(y_{max}=31\)时,
\(①t<-2\):
\[2t^2+4t+1=31 \]\[解得t_1=3, t_2=-5 \]其中,\(t_1=3\)不在范围内,舍去。
\(②t\ge-2\):
\[2(t+2)^2+4(t+2)+1=31 \]你猜我为什么不化完!
\[t_1+2=3, t_2+2=-5 \]\[解得t_1=1, t_2=-7 \]其中,\(t_2=-7\)不在范围内,舍去。
\[\therefore t的值为-5或1. \]
总结一下,取值范围类型的题目一般不太难,但前提是你画图分析!当技巧行不通时,永远记住画图是你最万能的法宝。
另外,如果是只有一个不等式的取值范围,如\(x<-2\)之类,也可以靠画图解决。事实上,它大概率只能靠画图解决。
二次函数中的函数思想(含参)
你发现这个标题看不懂,于是你继续往下读。
(\(2017\)南京中考改编)已知函数\(y=-x^2+(m-1)x+m\)(\(m\)为常数)。
\((1)\)求证:不论\(m\)为何值,该函数的顶点都在函数\(y=(x+1)^2\)的图像上。
\((2)\)当\(-2≤m≤3\)时,求该函数的图象的顶点纵坐标的取值范围。
你可能认为这个题目很简单,但无论如何还是先分析完。
\((1)\),证明嘛,按照他的思路,先把顶点表示出来。
提醒一下,之前的技巧在解答题里不能直接用!
接下来,题目转化为:
求证不论\(m\)为何值,点\((\frac {m-1} 2, \frac {(m+1)^2}4)\)都在函数\(y=(x+1)^2\)的图像上。
基本功了吧!判断一个点在不在图像上,就要把横坐标代入,看纵坐标一不一样。
你暗想这道题也没什么难度嘛,于是继续下一题。
\((2)\)有点绕吧,但是也没有难到那种程度。要顶点纵坐标的取值范围,无非就是把顶点纵坐标用\(m\)表示出来嘛。
到这里你应该知道了,\(y_V\)和\(m\)之间又套了一层函数关系,这就是这一节标题的意义。
题目转化为:
当\(-2≤m≤3\)时,求函数\(y_V=\frac {(m+1)^2}4\)取值范围。
取值技巧,启动!经过画图和计算,得到答案:
你又在暗想,这“函数思想”也没强到哪里去嘛!还不是轻轻松松就秒掉了。别急,好戏当然得在后面啊。
(\(2018\)南京改编)已知二次函数\(y=2(x-1)(x-m-3)\)(\(m\)为常数)。当\(m\)取什么值时,该函数的图像与\(y\)轴的交点在\(x\)轴上方?
太简单了吧!照他所说,就把二次函数和\(y\)轴的交点坐标表示出来呗!
在\(x\)轴上方,也就是
你还沉浸在秒杀题目的喜悦之中。下面再来一题。
\((1)\)若实数\(a,b\)满足\(a+b^2=2b+1\),则代数式\(a^2-4a+2b^2-4b-4\)的最小值为\(\_\_\_\)。
\((2)\)已知实数\(a,b\)满足\(a-b^2=4\),则代数式\(a^2-3b^2+a-14\)的最小值为\(\_\_\_\)。
嗯……两题都是两个未知数,让求最小值,不太现实。于是你立刻定下目标:消元!
先看第\((1)\)题,不知道用谁表示谁,就先看后面要求的代数式。不难发现,\(2b^2-4b\)和\(b^2-2b\)有联系,那就用\(a\)表示\(b^2-2b\),得:
代入原式,得:
就是求它最小值!干它!配方结束战斗!
还是那句话,趁热打铁,来看第\((2)\)题。一眼就是用\(a\)表示\(b^2\)。
代入原式,得:
全错。怎么样?惊不惊喜?意不意外?
别急,马上告诉你错哪儿了。
你是不是把代入完的代数式看成了一个函数?
看嘛,自变量是\(a\),函数值就是这个代数式的值!
那既然是函数,自变量的取值范围呢?
先说第\((2)\)题,\(b^2\ge 0\),那\(a\ge 4\)是必须的吧?
既然\(-3\)取不到,就应该另做考虑。简单验一下增减性,发现\(f(4)\)(即\(6\))才是最小值。
第\((1)\)题虽然没有明显的范围提示,但是看见化出的\(b^2-2b=1-a\)就应该警惕。\(b^2-2b\)没有取值范围吗?有的。
那么,刚刚配方得到的结果\((a-3)^2-11\)中,\(a=3\)就是取不到的,函数的取值范围限定在\(a\le 2\)。
题目于是转化为:
求\(y=(a-3)^2-11(a\le 2)\)的最小值。
用取值范围的技巧求得\(y\ge -10\)即可。
这样看来,函数思想还不容小觑,尤其是对于套了一层函数的,尤其要注意自变量的取值范围。这类范围一般隐蔽在条件中,如上两题换元时遇到的平方,难以发现。如果不把换完的代数式看成函数的话,就更想不到取值范围一回事了。
二次函数与方程(基础篇)
结论其实和你们预料的一样,先奉上。
一般地,二次函数\(y=ax^2+bx+c\)的图像与一元二次方程\(ax^2+bx+c=0\)的根有如下关系:
- 如果二次函数的图像与\(x\)轴有两个交点\((m,0)\)和\((n,0)\),那么方程有两个不相等的实数根\(x_1=m, x_2=n\)。
- 如果二次函数的图像与\(x\)轴只有一个交点\((m, 0)\),那么方程有两个相等的实数根\(x_1=x_2=m\)。
- 如果二次函数的图像与\(x\)轴没有交点,那么方程无实数根。
反之,根据一元二次方程根的情况,可以判断对应二次函数的图像与\(x\)轴的位置关系。
其实这一段话的本质是“交点\(↔\)联立方程组”。不信的话,可以梳理一下我们学过的坐标系交点问题,看一看本质是不是都是联立。
求直线和坐标轴的交点:
\[\left\{ \begin{aligned} &y=kx+b\\ &x(\text {or } y)=0\\ \end {aligned} \right. \]求直线和直线的交点:
\[\left\{ \begin{aligned} &y=k_1x+b_1\\ &y=k_2x+b_2\\ \end {aligned} \right. \]求直线和反比例函数图像的交点:
\[\left\{ \begin{aligned} &y=k_1x+b\\ &y=\frac {k_2}x\\ \end {aligned} \right. \](任意两个反比例函数图像之间都没有交点,且它们和坐标轴也没有交点。)
求抛物线和坐标轴的交点:
\[\left\{ \begin{aligned} &y=ax^2+bx+c\\ &x(\text {or } y)=0\\ \end {aligned} \right. \]
甚至还可以有:
求坐标轴和坐标轴的交点:(疑似瞎搞)
\[\left\{ \begin{aligned} &x=0\\ &y=0\\ \end {aligned} \right. \]解得:\(\left\{\begin{aligned}&x=0\\&y=0\\\end {aligned}\right.\),交点坐标为\((0,0)\)。(并非瞎搞)
求抛物线和直线的交点:
\[\left\{ \begin{aligned} &y=ax^2+bx+c\\ &y=kx+d\\ \end {aligned} \right. \]求抛物线和抛物线的交点:
\[\left\{ \begin{aligned} &y=a_1x^2+b_1x+c_1\\ &y=a_2x^2+b_2x+c_2\\ \end {aligned} \right. \]
然后解方程组,把两个方程右边连等,出几个解就有几个交点(在没有特殊取值范围的前提下),代入求\(y\),每一个点坐标就出来了。
课本规定,如果是函数图像和坐标轴交点,要写成如下形式:
本质还是联立,不是吗。但如果写成方程组应该也不会算错。
同样的,如果是解方程(组)的问题,有时也可以从“形”的角度看成函数图像的交点。这一块不再细讲,题目走起。
已知二次函数\(y=kx^2-7x-7\)的图像与\(x\)轴有两个交点,求\(k\)的取值范围。
哎呀太简单了吧!有两个交点说明\(b^2-4ac>0\),代入:
你要真这么答,遇到某些严格的老师,一整题的分就没喽。
怎么错的?那我问你,题目里的二次函数,加粗了还看不见?\(k\)要满足什么要求?
你感到不服,心里暗暗叫苦,\(****\)玩意儿,非得阴我,就是不讲武德!于是接着看下一题。
已知函数\(y=mx^2+3mx+m-1\)的图像与坐标轴恰有两个公共点,则实数\(m\)的值为\(\_\_\_\)。
假设你在考场上,你的思路大概会是这样的。
嗯,看上去不是难题,一分半秒杀,坐标轴恰有两个交点,说明是\(x,y\)两轴加起来两个,\(y\)轴自己肯定有且只有一个,原因很简单,当\(x=0\)时\(y\)肯定有值,那废话不多说,就是说和\(x\)轴只有\(1\)个交点,Wow这不是我刚背过的方程与函数关系吗,既然是二次函数,等等,这是二次函数吗,这不是,只说了函数,二次项还有系数,系数还没说不等于\(0\),哈哈哈发现坑了,分情况讨论,第一种\(m=0\),变成常函数\(y=-1\),和\(x\)轴没有公共点,排除,第二种\(m\ne 0\),也就是\(b^2-4ac=0\),恰好和\(x\)轴只有一个交点,列方程\((3m)^2-4m(m-1)=0\),赶紧解,说好的一分半马上要过了,化简得\(5m^2+4m=0\),秒得\(m_1=0\),哎呀不是说\(m\ne 0\)吗,划掉,第二个解\(m_2=-\frac 4 5\),正合我意,填上去,哎呀好险好险。
这就是考场上的头脑,一逗到底中间不带停顿的。说实话能想到函数分类讨论的已经很不错了,可惜后来要排除掉。
不过,这道题还有坑,非常深,我当时也是到最后才发现。
请问,\(y\)轴上的那个交点一定是\(y\)轴的吗?为什么不能是\(x,y\)轴的公共点呢?
哦,布豪,过原点的没算上,也就是当\(x=0\)时\(y=0\),得到条件\(m-1=0\Rightarrow m=1\),验算一手,\(y=x^2+3x\),过原点,而且交点分别是\((0,0)\)和\((-3,0)\),完全符合条件,答案是\(-\frac 4 5\)或\(1\),Perfect!
没想到吧,如果真的那么骂,不管什么题都是出题老师在背后阴你了。所以说,还是得多考虑一手,说不定\(3\)分就回来了呢。
再下面一题就没有坑了,我保证!
二次函数\(y=ax^2+bx+c(a\ne 0)\)的图像如图所示。
若方程\(ax^2+bx+c=k\)有两个不相等的实数根,求\(k\)的取值范围。
我跟你说,遇到这种函数和方程长得像,但又不是完全一样的这种情况,就把函数往方程上凑,或者方程往函数上凑。对于这道题,转化的方法有两种。
- 注意到\(ax^2+bx+c=k\Rightarrow ax^2+bx+c-k=0\)。由此理解为:函数\(y=ax^2+bx+c\)向下平移\(k\)个单位所得的图像和\(x\)轴的交点。有两个不相等的实数根,就是说交点有两个。容易发现,只要\(k<2\)即可。\(k=2\)的情况你可以看一下,正好只有一个交点,不满足要求。
- 注意到\(ax^2+bx+c=k\)可以理解为:函数\(y=ax^2+bx+c\)和\(y=k\)的交点。有两个不相等的实数根,就是说交点有两个。容易发现,只要\(k<2\)即可。\(k=2\)的情况你可以看一下,正好只有一个交点,不满足要求。
(怎么有一股淡淡的人机感)你看,本质是一样的。
常见坑汇总
由二次函数两半增减性不同引申出如下坑:
- 给出\(x\)的取值范围时故意跨过顶点。
- 不给你\(x\)的取值范围,给\(y\)的,这种有时双答案。
- 不定取值范围(提高篇例题)时,顶点左右最值可能需要分类讨论。
以上坑的共同对策是画图。
由换元类题目或函数思想引申出如下坑:
- 自变量的取值范围隐藏在另一个自变量里。
对策是把式子看成函数,仔细寻找自变量的取值范围。
由题目文字游戏引申出以下坑:
-
“双圈问题”。
仿照一元二次方程,这类题目通常在二次函数和函数的说法之间切换,把实数根的说法换成与\(x\)轴的交点即可。以下是它们的例题对比:已知方程\(y=kx^2-7x-7\)有两个不等的实数根,求\(k\)的取值范围。
已知二次函数\(y=kx^2-7x-7\)的图像与\(x\)轴有两个交点,求\(k\)的取值范围。
对策如下:
如果二次项系数不含参,那放心做,必须是二次函数。
如果二次项系数含参,再看第一个圈里的内容。
- 第一个圈是二次函数的话,先写下二次项系数不等于\(0\),以防后面忘掉,然后正常做题,最后带上这个条件即可。
- 第一个圈是函数的话,分类讨论二次项系数是不是\(0\),务必记住后面要把两种情况合起来。
二次函数与方程(提高篇)
——交点、联立在大题和压轴题中的运用
先上个有难度的。仅做拓展!
思考:方程\(|x^2-2x-3|=2x+b\)解的个数。
管它什么方程,来个硬碰硬看看!
\(①x^2-2x-3> 0\),即\(x<-1\)或\(x>3\)时:
原方程可化为:
\[x^2-2x-3=2x+b \]整理,得:
\[x^2-4x-(b+3)=0 \]这里容我偷个懒,把\(\Delta\)借过来用。
\[\Delta=(-4)^2-4\cdot (-b-3)=4b+28 \]讨论\(\Delta\)和\(0\)的大小关系。
\(1\degree \Delta>0\),即\(x>-7\)时,求出两个实数根:
\[x=\frac {-b±\sqrt {\Delta}} {2a}=\frac {4±\sqrt{4b+28}} 2=2±\sqrt {b+7} \]\[\therefore x_1=2+\sqrt {b+7}, x_2=2-\sqrt {b+7} \]\[\dots \]
好吧,看到后面还有\(\Delta\)两种情况,绝对值内一种情况,\(x\)和\(b\)的关系还理不清,是时候换种思路了。
哦?之前好像讲过,解方程可以用“形”的方法考虑的来着。把等式左右看成函数!
画出图像。\(y_1\)的图像有点难画,不过没关系!绝对值得特性我们已经探究过了,这里复习一下。
对于绝对值函数\(y=|f(x)|\)(这里的\(f(x)\)指任意的函数运算,因为我们并不知道绝对值里面是什么,所以统一用\(f(x)\)代替,意思是自变量\(x\)进行一次规定的函数运算。它可以是\(kx+b\)、\(\frac k x\)、\(ax^2+bx+c\)等),可以拆分成一个分段函数:
\[\left\{ \begin{aligned} &y=f(x)&f(x)\ge 0\\ &y=-f(x)&f(x)<0\\ \end{aligned} \right.\]容易发现,其图像在\(x\)轴上半部分(\(y\ge 0\))是\(y=f(x)\)的图像,而剩余部分是\(y=-f(x)\)的图像。
不难得到,\(y=-f(x)\)的图像和\(y=f(x)\)关于\(x\)轴对称。简易证明如下:
设\(y=-f(x)(x<0)\)上有一点\((t, -f(t))\)。
其对称点\((t, f(t))\)显然在\(y=f(x)\)图像上。得证。
代到现在,\(y_1\)的函数图像在\(x\)轴上半部分是\(y=x^2-2x-3\)的图像,而剩余部分则把\(y=x^2-2x-3\)沿\(x\)轴翻折即可,也就是\(y=-x^2+2x+3\)的图像。(记住!后面要考)
轻松画出来。\(y_2\)就更简单了,“移一移”即可。



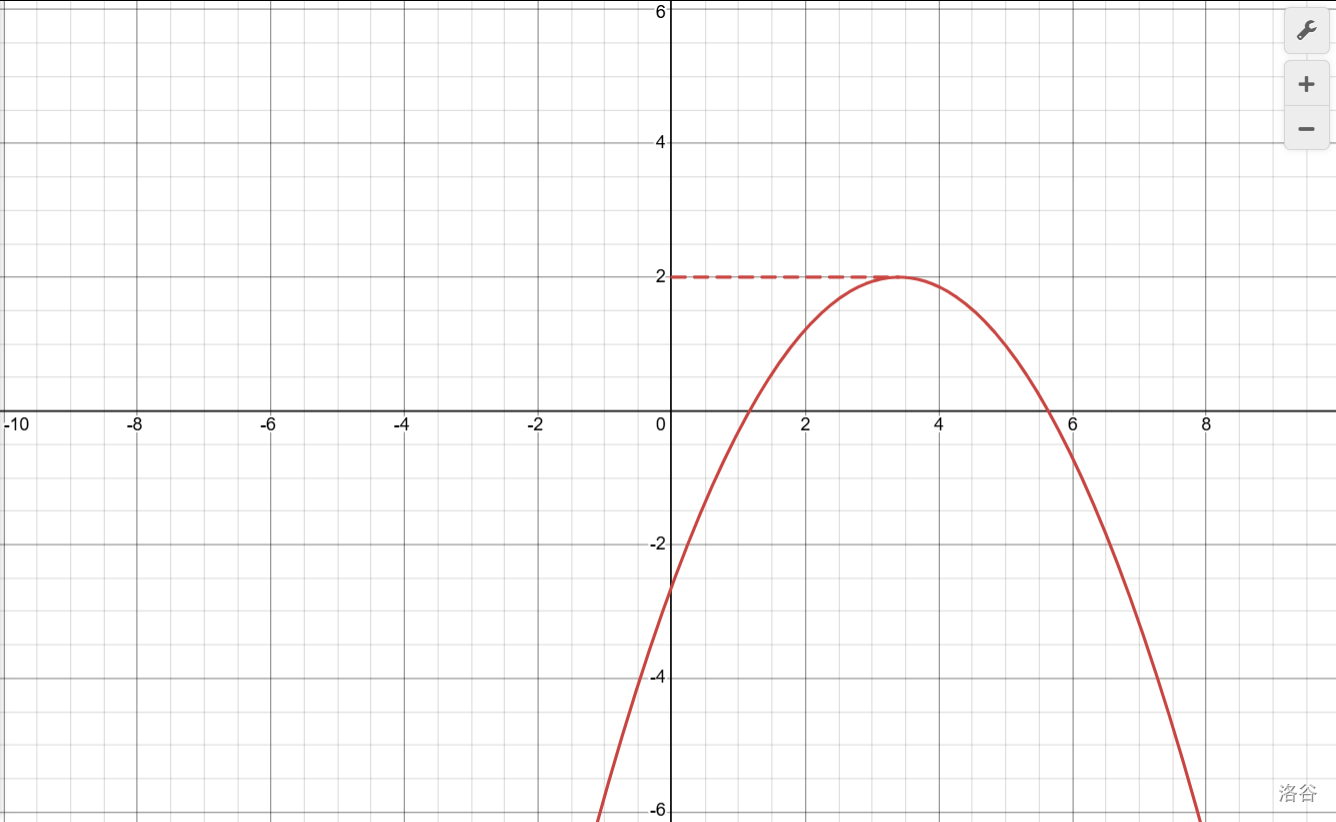

 浙公网安备 33010602011771号
浙公网安备 33010602011771号