初识二次函数

仅需通晓初二及其前置知识，和一元二次方程即可学习。

引入：从方程到函数

回顾我们学习一次函数的时候，探讨了一次函数和一元一次方程的关系，例如一次函数\(y=kx+b(k\neq 0)\)和\(x\)轴交点横坐标就是方程\(kx+b=0\)的解等等。

那么，我们已经学习了一元二次方程，从一次代数的学习正式跨入了二次。那么，你能否想到一种函数，使其与一元二次方程的关系和一次函数与一元一次方程的关系类似呢？

定义：你猜这块考什么

形如\(y=ax^2+bx+c(a,b,c为常数, a\neq 0)\)的函数叫作二次函数（\(\text {quadratic function}\)）。

相信同学们一眼就能看出这句话里哪些词最重要。

• \(y=ax^2+bx+c\)是二次函数的定义式，肯定重要。
• 但是考试经常考的，和一次函数一样容易错的，必定是\(a\neq 0\)。

备注：如果函数可以化成二次函数的定义式而且定义域（怎么又说错了）取值范围不变的话，其也是二次函数。

这块有一次函数的一元二次方程的经验，就不赘述了。

性质探究：从反比例到二次

都知道下一步要做什么吧😉

不过，为了降低难度，我决定把定义式\(y=ax^2+bx+c\)先换成特殊情况（\(a=1,b=c=0\)）：\(y=x^2\)。

现在，探究以下问题：

1. 画出\(y=x^2\)的图像。
2. 其图像是一条直线吗？请说明理由。
3. 增减性如何？请证明。
4. 对称性如何？请证明。
5. 有最大 / 最小值吗？是多少？
6. 你觉得图像里有某个特殊点吗？

每一个都奇长无比，不过我们还是得证，证完就更容易记住，并且可以由证明过程引申很多。

直线还是曲线？

通过描几个点，我们很容易发现它们都不在一条直线上。

\(x\)	\(1\)	\(-1\)	\(2\)
\(y\)	\(1\)	\(1\)	\(4\)

但是我们不能以偏概全，要想证明它整体的图像是个曲线，就要仿照反比例函数。

有三个二次函数上的点前来\(\_\_\)。我们设为\(A(a, a^2)\)，\(B(b, b^2)\)，\(C(c, c^2)\)。不妨设\(a<b<c\)，其实这一步是要排除\(a=b=c\)的情况。

法\(1\)：距离公式爆肝\(AB+BC>AC\)

这种方法我是试过的，你也可以试试。到最后一堆根号化不完，在目前看来这种情况必须舍去。可谓是“试试就逝世”。

法\(2\)：\(k_{AB}\neq k_{BC}\)

这种方法还是和以前一样好用啊。

\[k_{AB}=\frac {\Delta y}{\Delta x}=\frac {b^2-a^2}{b-a}=\frac {(b+a)(b-a)} {b-a}=b+a \]

（这句要讲清因为\(a<b\)才可以把\(b-a\)约掉的。）

\[k_{BC}=\frac {\Delta y}{\Delta x}=\frac {c^2-b^2}{c-b}=\frac {(c+b)(c-b)} {c-b}=c+b \]

（同理。）

\[\because a<c\therefore b+a<c+b \]

\[k_{AB}\neq k_{BC} \]

\[\therefore 图像上任意三点都不在一条直线上 \]

\[\text {Q.E.D.} \]

注中注：\(\text {Q.E.D.}\)是证明完毕的意思。考试不要用啊！被老师骂了别找我。

接下来给各位引入一种新方法。它比法\(2\)更快，并且可以直接解决一般定义式（\(y=ax^2+bx+c\)）的证明！

法\(3\)：一元二次方程，启动！

假设有一条直线\(y=kx+d(k\neq 0)\)，满足二次函数\(y=ax^2+bx+c(a\neq 0)\)上至少三个点在直线上。如果我们找不出这样的一条直线，则二次函数图像必定非直线。

联立。

\[\left\{ \begin{aligned} &y=kx+d \\ &y=ax^2+bx+c\\ \end{aligned} \right. \]

右侧连等，我们的目的是找到连等后方程解的个数，根据我们探究出的方程与函数关系，就可以看出直线与二次函数交点的个数。

\[ax^2+bx+c=kx+d \]

注意到是一元二次方程，因此整理：

\[ax^2+(b-k)x+(c-d)=0\ \ \ \ (a\neq 0) \]

这个一元二次方程全是参数，我们无法确定\(b^2-4ac\)的大小，但是我们可以肯定，

这个方程最多只有两个解。

\[\text {耶！反证法得了MVP！} \]

因此我们只能用平滑的曲线去连接我们描出的点。画出来以后像物理中的抛物线（参见物理必修二：抛体运动），那就把二次函数的图像叫作：

抛物线（\(\text {parabola}\)）。

增减性

画出图像以后我们就很轻松地看出来了。

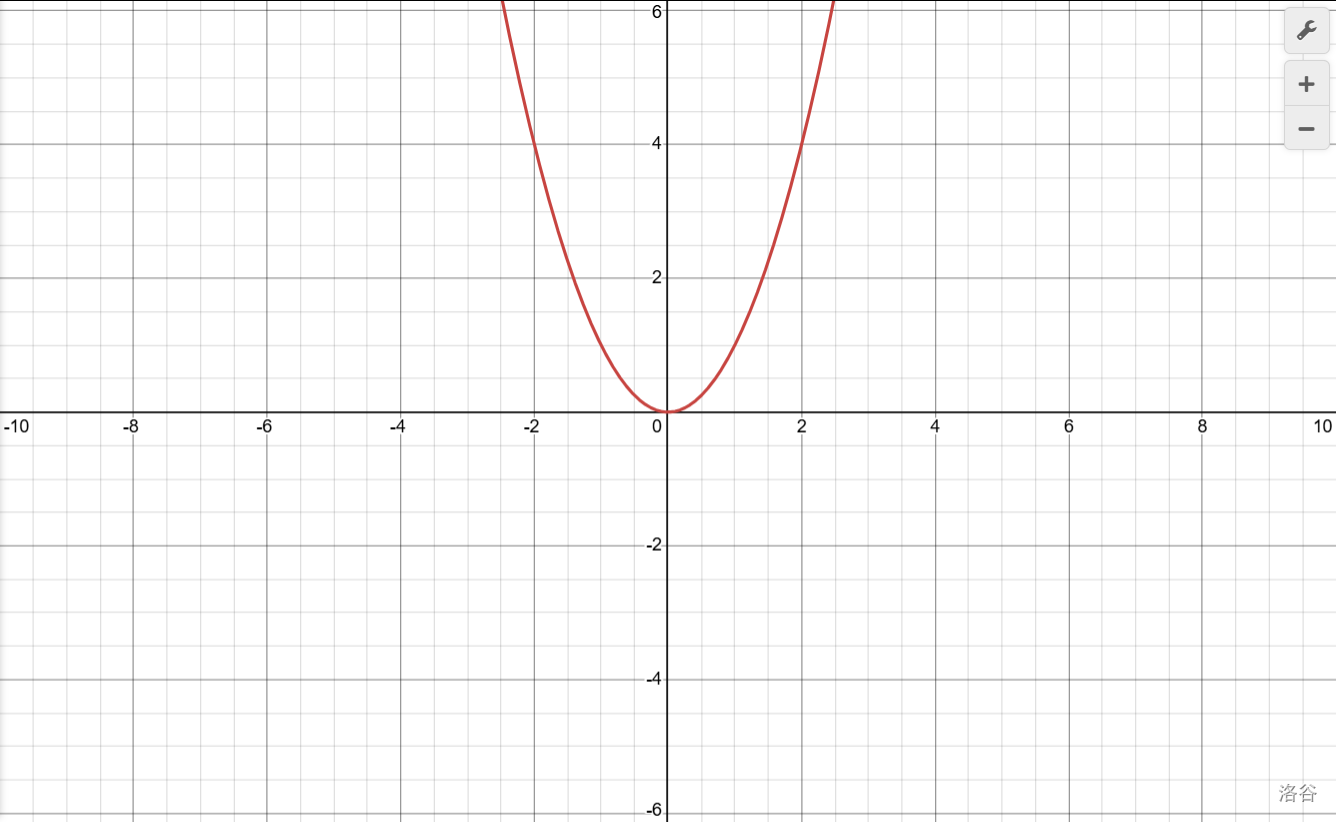
哎呀这不就是当\(x<0\)时\(y\)随\(x\)增大而减小\(x>0\)时候\(y\)随\(x\)增大而增大嘛！

上面这句话里有两个问题。

• 只讨论了\(x<0\)和\(x>0\)两种情况，那\(x=0\)呢？归谁？
• 证明呢？你说的谁信啊（也就改卷老师不信）。

那我们改一下，把等于\(0\)归到大于\(0\)里面，顺便证明一手。

设抛物线上两点\(A(a, a^2)\)，\(B(b, b^2)\)，且\(a<b\)。

\(①x<0\)，即\(a<b<0\)：

根据我们之前的思路，我们只要证明\(a^2>b^2\)就行了。

\[\because a^2-b^2=(a+b)(a-b); \]

\[a<0, b<0\Rightarrow a+b<0; \]

\[a<b\Rightarrow a-b<0; \]

\[\therefore (a+b)(a-b)>0 \]

\[\therefore a^2>b^2 \]

\[\text {Q.E.D.} \]

\(②x\geq 0\)，即\(0\leq a<b\)：

同理，只需证\(a^2<b^2\)即可。

\[\because a^2-b^2=(a+b)(a-b); \]

\[a>0, b\geq 0\Rightarrow a+b>0; \]

\[a<b\Rightarrow a-b<0; \]

\[\therefore (a+b)(a-b)<0 \]

\[\therefore a^2<b^2 \]

\[\text {Q.E.D.} \]

对于抛物线\(y=x^2\)：

• 当\(x<0\)时，\(y\)随\(x\)增大而减小；
• 当\(x\geq 0\)时，\(y\)随\(x\)增大而增大。

对称性

借一手之前的图。

容易看出，抛物线关于\(y\)轴对称。证明：

设抛物线上一点\(A(a, a^2)\)。

其关于\(y\)轴的对称点为\(A'(-a, a^2)\)。

\[\because (-a)^2=a^2 \]

\[\therefore 点A'在抛物线上 \]

\[\therefore y=x^2图像关于y轴对称 \]

没有其它对称轴了。那么，思考所有抛物线都关于\(y\)轴对称吗？如果不是，它们的对称轴分别是哪条直线？

最值（取值范围）

\[\because x^2\ge 0 \]

\[\therefore 当x=0时，y=x^2有最小值为0 \]

或者可以写成：

\[对于函数y=x^2，当x=0时，y_{min}=0 \]

这里我们利用平方的非负性解决（记住了！后面要考）。

另外，

• 自变量\(x\)的取值范围是全体实数；
• 函数\(y\)的取值范围是\(y\geq 0\)。

特殊点

如果你现在仍然判断不出来哪个点是特殊点，请按照以下思路思考：

• 一次函数中\(y\)有最值吗？
• 反比例函数中\(y\)有最值吗？
• 二次函数中\(y\)有最值吗？有，那最值点是哪一点？

我们刚刚说当\(x=0\)时\(y_{min}=0\)，因此该最小值对应图像上的一个点，即\((0, 0)\)。

我们看看该点包含了哪些信息。

• 有了这个点你可以大致确定抛物线的位置。
• 该点左侧\(y\)随\(x\)增大而减小，右侧相反。
• 该点通过的垂直于\(x\)轴的直线是抛物线的对称轴。
• 该点是最值点，在\(y=x^2\)中是最小值。
• ……

可以看出这个点很重要。我们把它称为顶点（\(\text {vertex}\)）。

从图像来看，这个名字是很形象的。

推广：从特殊到一般

直线还是曲线？（一般定义式）

这一段没有什么思维含量，所以直接给过程。

设抛物线\(y=ax^2+bx+c(a\neq 0)\)上有三点\(A(x_1, ax_1^2+bx_1+c), B(x_2, ax_2^2+bx_2+c), C(x_3, ax_3^2+bx_3+c)\)，且\(x_1<x_2<x_3\)。

考虑法\(2\)，证明\(k_{AB}\neq k_{BC}\)。

\[k_{AB}=\frac {(ax_2^2+bx_2+c)-(ax_1^2+bx_1+c)} {x_2-x_1} \]

\[=\frac {a(x_2+x_1)(x_2-x_1)+b(x_2-x_1)} {x_2-x_1} \]

\[\because x_2>x_1\Rightarrow x_2-x_1>0 \]

\[\therefore k_{AB}=a(x_2+x_1)+b \]

\[k_{BC}=\frac {(ax_3^2+bx_3+c)-(ax_2^2+bx_2+c)} {x_3-x_2} \]

\[=\frac {a(x_3+x_2)(x_3-x_2)+b(x_3-x_2)} {x_3-x_2} \]

\[同理，k_{BC}=a(x_3+x_2)+b \]

\[x_1<x_3\Rightarrow x_1+x_2<x_3+x_2 \]

\[\Rightarrow x_1+x_2\neq x_3+x_2 \]

\[\because a\neq 0 \]

\[\therefore a(x_2+x_1)+b\neq a(x_3+x_2)+b \]

\[k_{AB}\neq k_{BC} \]

\[\text {Q.E.D.} \]

接下来让我们换个顺序，先把最值研究掉。

最值（一般定义式）

当时说后面要考的东西，你还记得吗？

利用平方的非负性，可以快速求出最大值或最小值。

我们先举个特例，\(y=2x^2+4x-4\)，它有平方吗？
类似的话你可能在哪里看过。没错，就是这里。

配方法：耶！我的用武之地！

\[y=2x^2+4x-4 \]

\[=2(x^2+2x-2) \]

\[=2(x^2+2x+1-3) \]

\[=2(x+1)^2-6 \]

容易看出，当\(x=-1\)时，\(y_{min}=-6\)。

这种是简单的配方，全程不出现分数的那种。如果出现分数，这种过程很明显会耗时间（因为常数项先并进括号再乘出去，运算了两次）。因此，遵循大道至简的原则，我们把单纯的配方法压成两步：

\[y=2(x^2+2x+1^2)-4-2\times 1 \]

\[y=2(x+1)^2-6 \]

几个问题明确一下。

• 内心\(\text {OS}\)步骤描述：

思考	写到的步骤
把\(2\)提取出来	\(=2(x^2+2x\)
配完全平方式（一次项一半平方）	\(=2(x^2+2x+1^2)\)
常数项照抄	\(=2(x^2+2x+1^2)-4\)
后面减掉多配的常数项，分配律乘出来	\(=2(x^2+2x+1^2)-4-2\times 1\)
整理，一步得结果	\(=2(x+1)^2-6\)

• 注意！括号内\(1^2\)是为了后面变成平方时方便。如果我们配出的常数项是\((\frac {25} {16})^2=\frac {625}{256}\)，再把\(\frac {625}{256}\)填进括号，第二步又要开方，非常麻烦。
• 括号外\(1\)是为了后面计算方便。事先在配完全平方式时就把常数项算好，整理时就可以直接乘，减少出错的可能性。
• 脑子必须跟上你的手。相信你亲手做一题就明白了。

练习：配方法求函数\(y=x^2-3x+4\)的最值。

参考答案：\(\textcolor{grey}{当x=\frac 3 2时，y_{min}=\frac 7 4。}\)

顶点和顶点式

在上面的特例中，显然该抛物线的顶点就是\((\frac 3 2, \frac 7 4)\)。现在，让我们从特殊到一般，探究一下\(y=ax^2+bx+c(a\neq 0)\)的顶点坐标和最值。

很简单，就是把配方的过程换成纯字母嘛。照样两步！

\[y=a[x^2+\frac b ax+(\frac b {2a})^2]+c-a\times \frac {b^2} {4a^2} \]

\[y=a(x+\frac b {2a})^2+\frac {4ac-b^2} {4a} \]

抛物线\(y=ax^2+bx+c(a\neq 0)\)的顶点坐标为\((-\frac b {2a}, \frac {4ac-b^2} {4a})\)。

再讨论一下最值。为什么用“讨论”，应该是很清楚的。

\(①a>0\)：当\(x=-\frac b {2a}\)时，\(y_{min}=\frac {4ac-b^2} {4a}\)；

\(②a<0\)：当\(x=-\frac b {2a}\)时，\(y_{max}=\frac {4ac-b^2} {4a}\)。

最后，隆重介绍一下，我们刚刚化出来的形式

\[y=a(x+\frac b {2a})^2+\frac {4ac-b^2} {4a} \]

就是苏科版课本第二种，也是最后一种承认的二次函数形式：

顶点式（\(\text {vertex form}\)）。

由于某些原因（做题你就明白了），它在实际运用中一般写成

\[y=a(x+h)^2+k \]

增减性（一般定义式）

根据假设，抛物线顶点左侧（即\(x<-\frac b {2a}\)时），\(y\)随\(x\)的增大而减小；右侧（即\(x\ge -\frac b {2a}\)时）相反。

设抛物线\(y=ax^2+bx+c(a\neq 0)\)上有两点\(A(m, am^2+bm+c), B(n, an^2+bn+c)\)，且\(m<n\)。

\[(am^2+bm+c)-(an^2+bn+c) \]

\[=a(m^2-n^2)+b(m-n) \]

\[=a(m+n)(m-n)+b(m-n) \]

\[=(m-n)[a(m+n)+b] \]

\(①m<n<-\frac b {2a}\)：

\[\because m<-\frac b {2a}, n<-\frac b {2a}\Rightarrow m+n<-\frac b a; \]

\[\Rightarrow a(m+n)+b\dots \]

等等！\(a\)的正负决定了这个多项式的正负！还要讨论。

\(1\degree a>0\)：

\[\Rightarrow a(m+n)+b<a\cdot (-\frac b a)+b=0 \]

\[m<n\Rightarrow m-n<0; \]

\[\therefore (m-n)[a(m+n)+b]>0 \]

\[\therefore am^2+bm+c>an^2+bn+c \]

\[y随x的增大而减小 \]

\(2\degree a<0\)：

\[\Rightarrow a(m+n)+b>a\cdot (-\frac b a)+b=0 \]

\[m<n\Rightarrow m-n<0; \]

\[\therefore (m-n)[a(m+n)+b]<0 \]

\[\therefore am^2+bm+c<an^2+bn+c \]

\[y随x的增大而增大 \]

\(②-\frac b {2a}\leq m<n\)：

\[\because m\ge -\frac b {2a}, n>-\frac b {2a}\Rightarrow m+n>-\frac b a; \]

\(1\degree a>0\)：

\[\Rightarrow a(m+n)+b>a\cdot (-\frac b a)+b=0 \]

\[m<n\Rightarrow m-n<0; \]

\[\therefore (m-n)[a(m+n)+b]<0 \]

\[\therefore am^2+bm+c<an^2+bn+c \]

\[y随x的增大而增大 \]

\(2\degree a<0\)：

\[\Rightarrow a(m+n)+b<a\cdot (-\frac b a)+b=0 \]

\[m<n\Rightarrow m-n<0; \]

\[\therefore (m-n)[a(m+n)+b]>0 \]

\[\therefore am^2+bm+c>an^2+bn+c \]

\[y随x的增大而减小 \]

是的，证明过程就是巨长无比。

结论：对于抛物线\(y=ax^2+bx+c(a\neq 0)\)：

• 当\(a>0\)时：
  • 当\(x<-\frac b {2a}\)时，\(y\)随\(x\)增大而减小；
  • 当\(x\ge -\frac b {2a}\)时，\(y\)随\(x\)增大而增大；
• 当\(a>0\)时：
  • 当\(x<-\frac b {2a}\)时，\(y\)随\(x\)增大而增大；
  • 当\(x\ge -\frac b {2a}\)时，\(y\)随\(x\)增大而减小；

看来有的时候，我们的假设也会出现错误，这是不可避免的。验证或推翻假设的方法除了证明，还有画图。通过图像我们可以直观看出函数\(y=-2x^2+3x+4\)的增减性与我们最初的猜想不符。

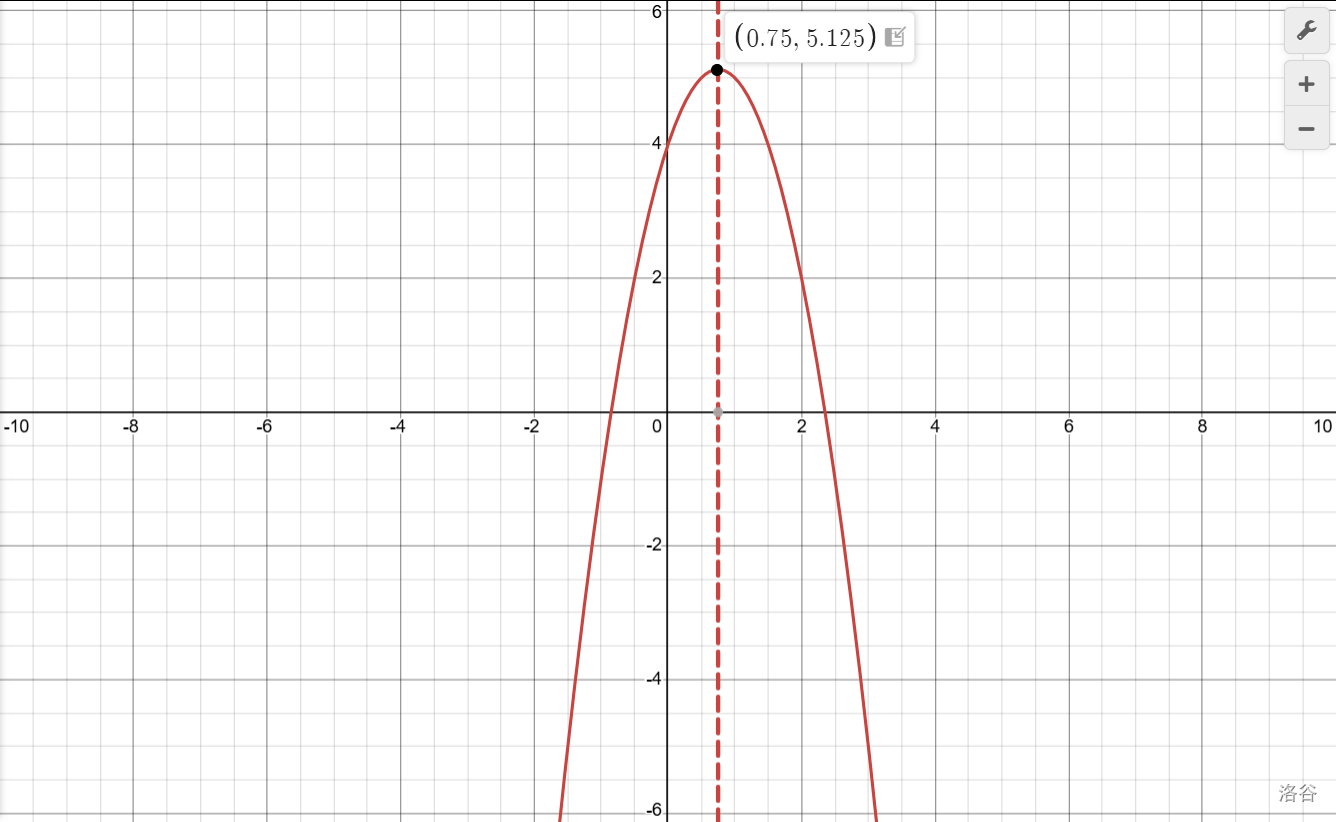
对称性（一般定义式）

根据假设，我们认为抛物线的对称轴为通过其顶点的垂直于\(x\)轴的直线，即直线\(x=-\frac b {2a}\)。

设抛物线\(y=ax^2+bx+c(a\ne 0)\)上有一点\(A(m, am^2+bm+c)\)。

点\(A\)关于直线\(x=-\frac b {2a}\)的对称点是……

算了，如果你没学过口诀（中间两倍减头）的话，那还是老老实实设成\(A'(x, am^2+bm+c)\)。根据中点公式，有：

\[\frac {m+x} 2=-\frac b {2a} \]

\[x=-\frac b a-m=-\frac {am+b} a \]

\[\therefore A'(-\frac {am+b} a, am^2+bm+c) \]

\[\because a(-\frac {am+b} a)^2+b(-\frac {am+b} a)+c \]

\[=\frac {(am+b)^2} a-\frac {b(am+b)} a+c \]

\[=\frac {a^2m^2+2abm+b^2-abm-b^2} a+c \]

\[=\frac {a(am^2+bm)} a+c \]

\[a\neq 0\Rightarrow 原式=am^2+bm+c \]

\[\therefore 点A'在直线x=-\frac b {2a}上 \]

\[\text {Q.E.D.} \]

开口大小和方向

拿书上的探究举例子吧，我们研究\(y=ax^2(a\ne 0)\)的图像随\(a\)取值变化的变化情况。

准备好我们的实验器材方格纸，打好坐标系。

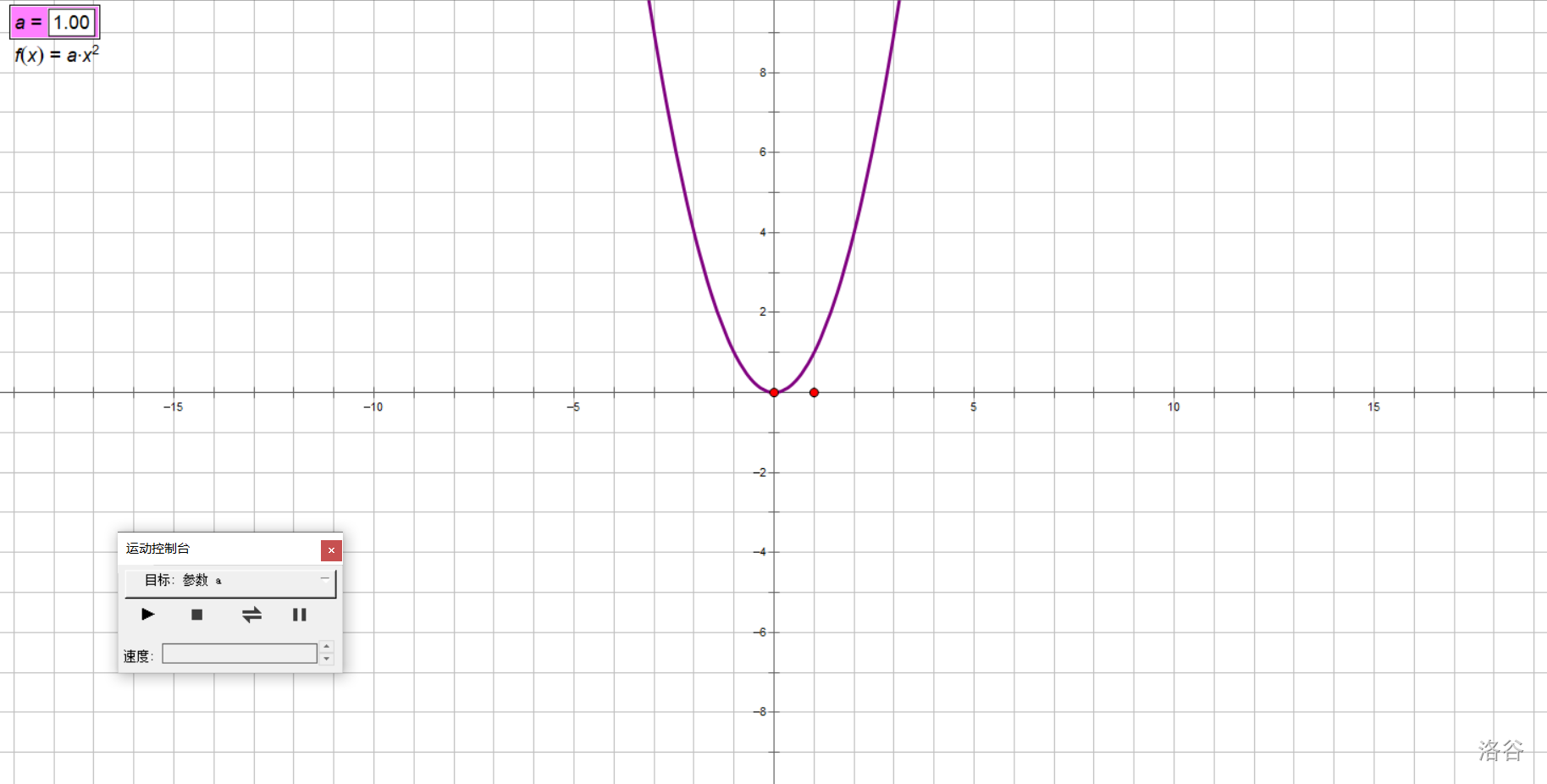
让\(a\)动起来！

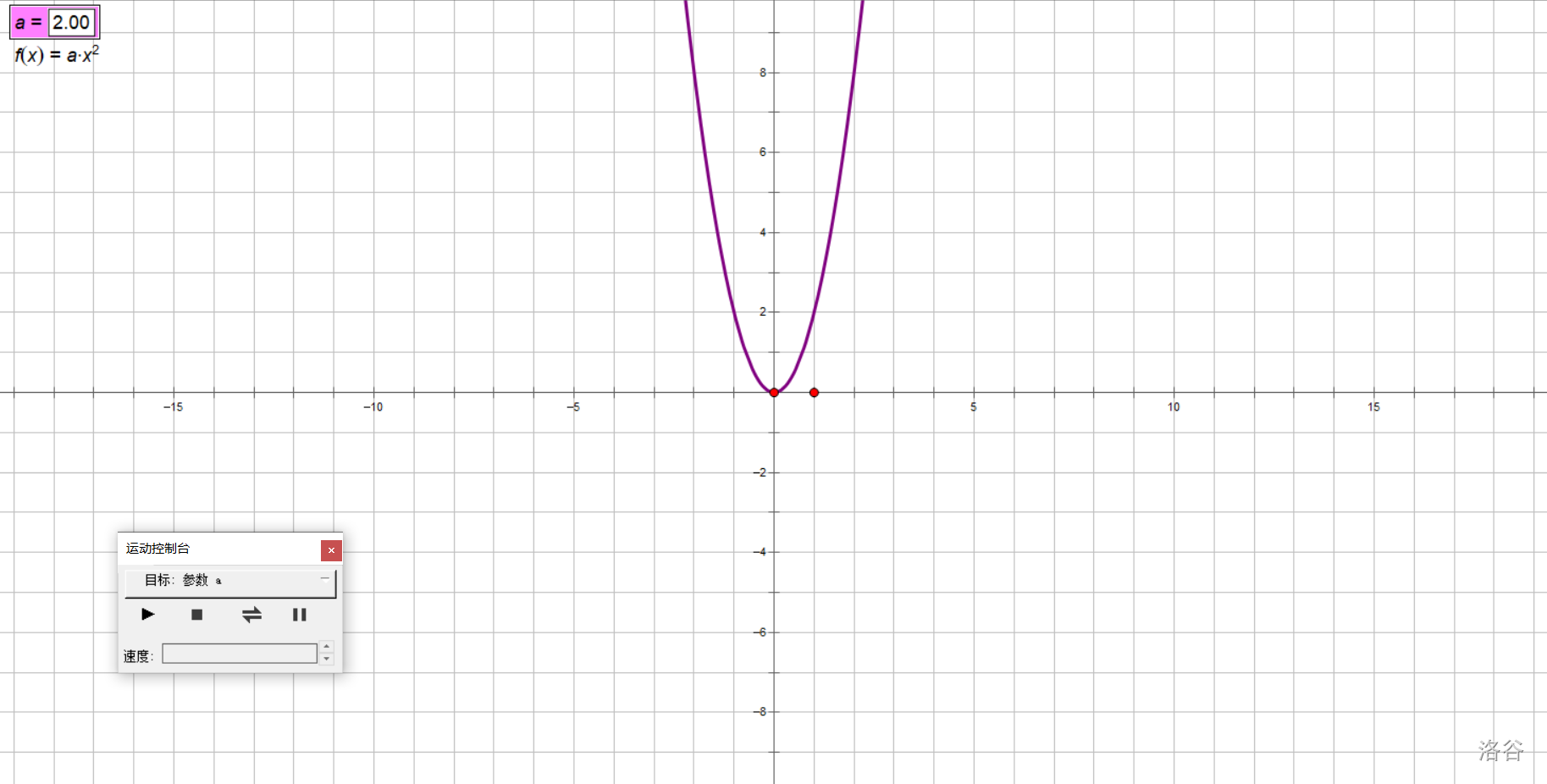
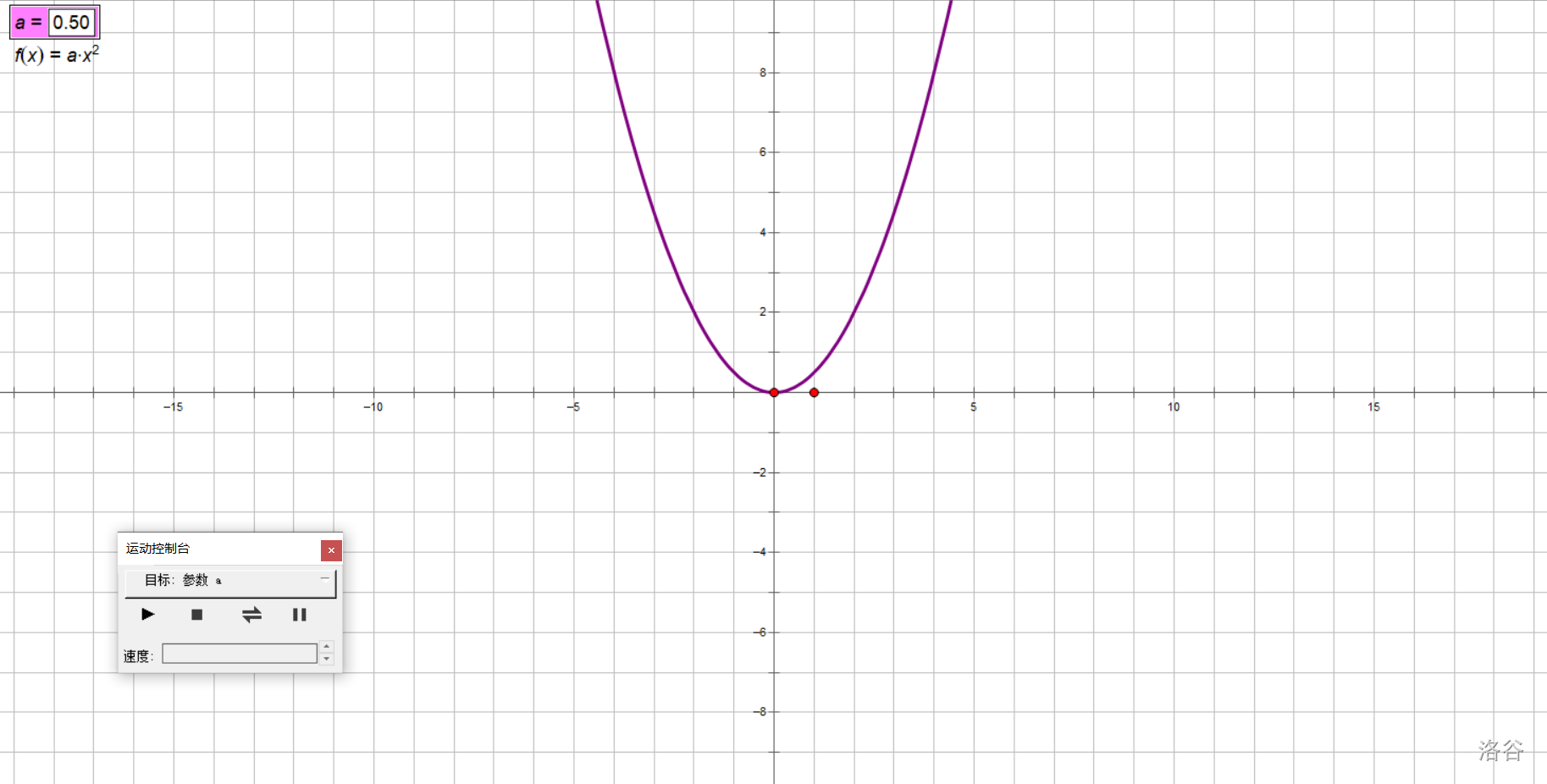
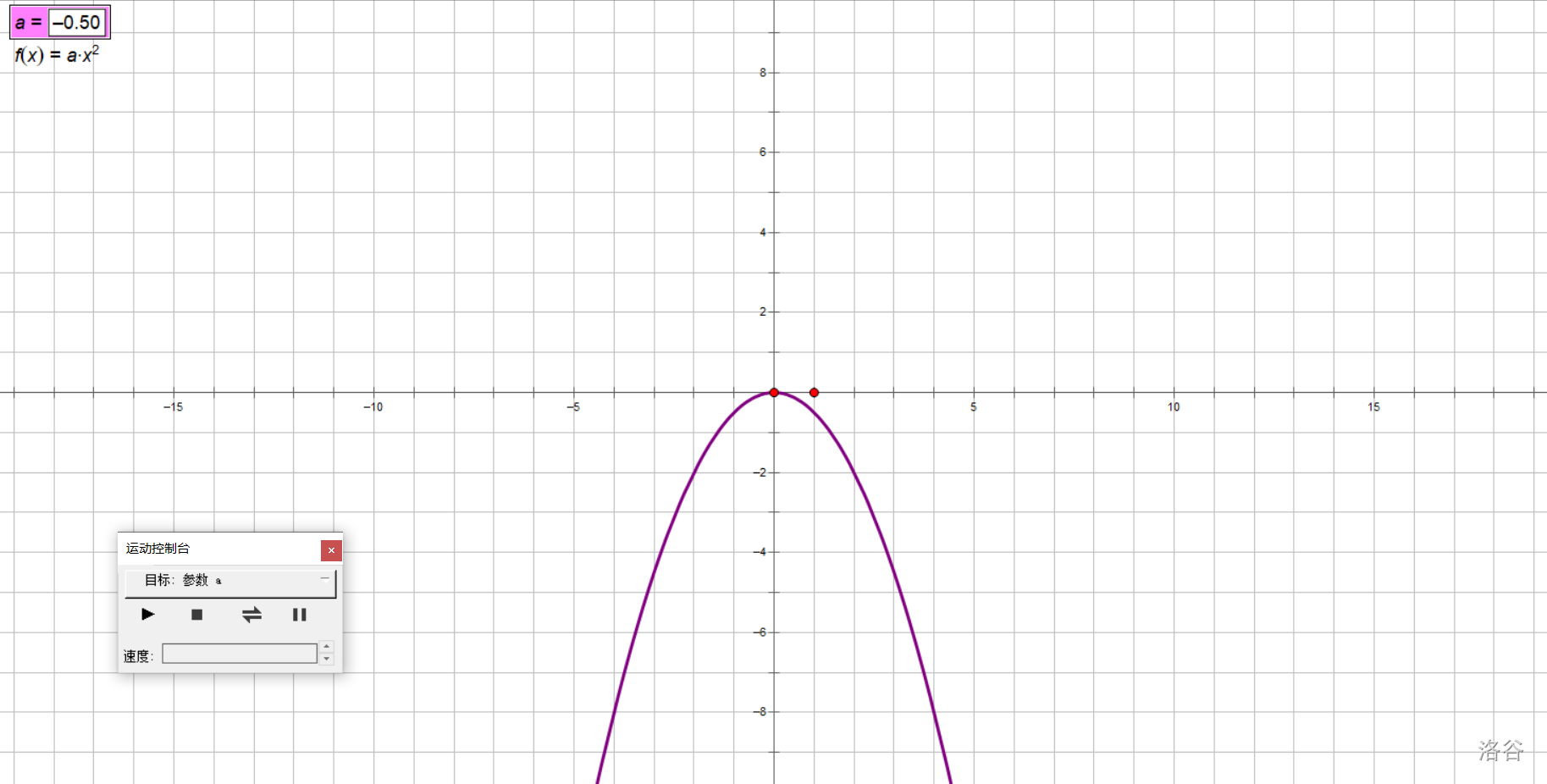
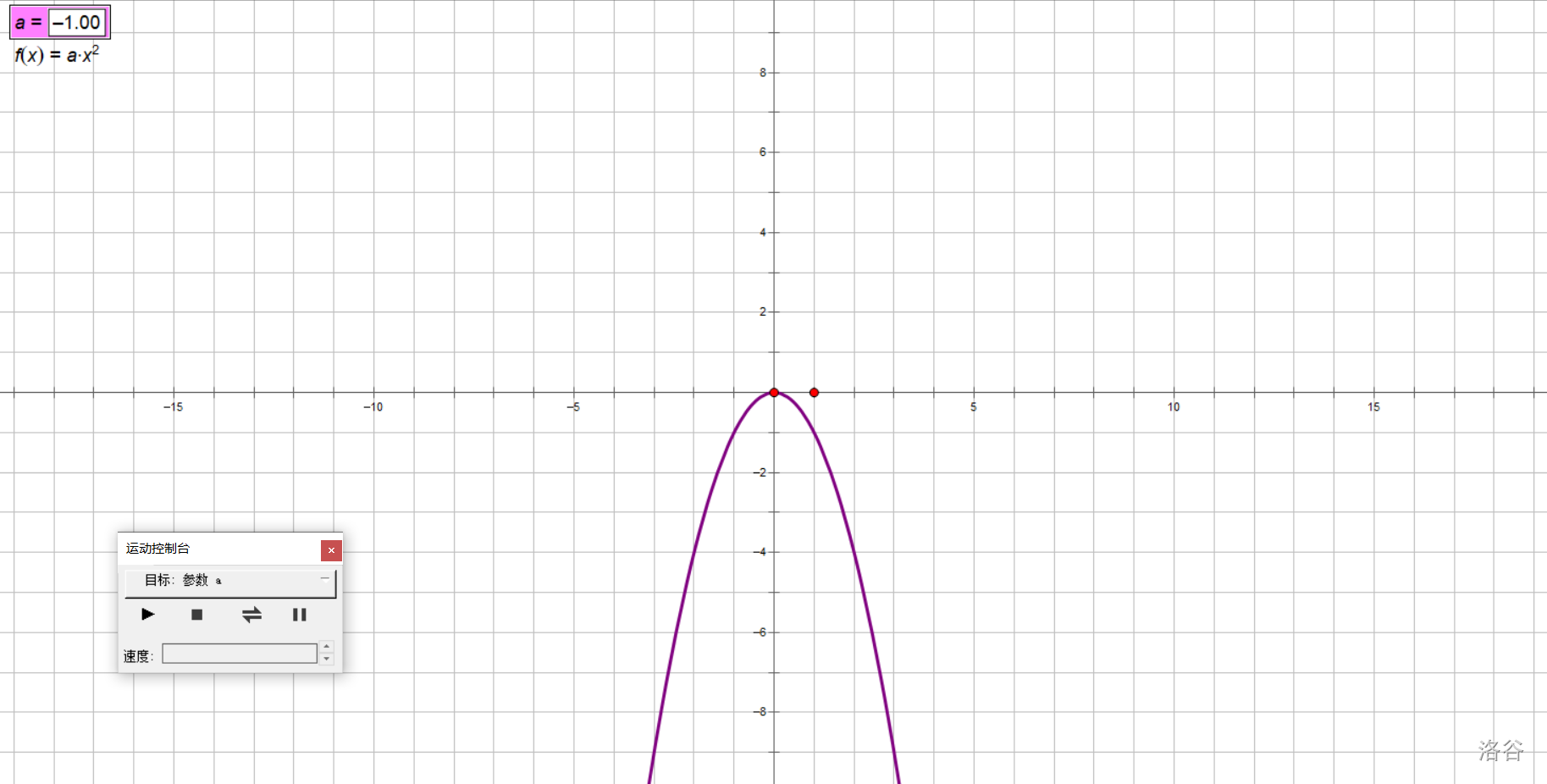
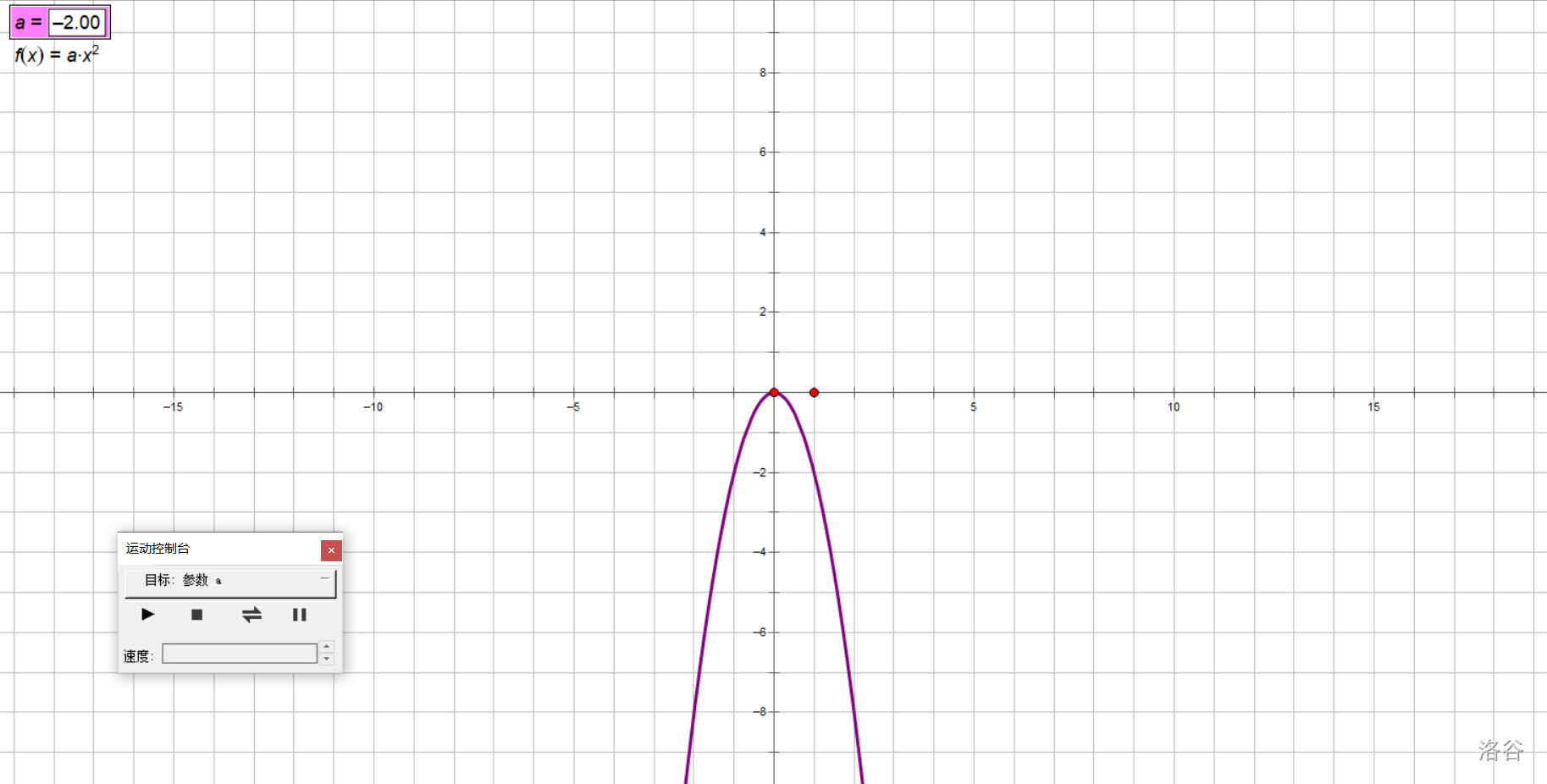
在实验中，我们让\(a\)从大到小，从正到负变化，得出以下结论：

对于抛物线\(y=ax^2(a\neq 0)\)：

• 当\(a>0\)时，开口朝上，\(a\)越小，开口越大；
• 当\(a<0\)时，开口朝下，\(a\)越大，开口越大。

两句话的后半部分可以合并为：

• （无论\(a\)正负）\(|a|\)越小，开口越大；\(|a|\)越大，开口越小。

至于这个结论能否应用于所有的抛物线中，请听下回分解。

变换：“移一移”

左加右减，上加下减，大道也。

函数\(y=(x+3)^2\)的图像和函数\(y=x^2\)的图像有什么关系？
聪明的你一定能想到，向左平移了\(3\)格。

那函数\(y=2(x+3)^2\)的图像和\(y=2x^2\)的有什么关系？
那当然还是向左平移了\(3\)格。

上难度！函数\(y=2(x+3)^2+114514\)和\(y=2x^2\)呢？
根据“大道”，显然是向左平移\(3\)格，向上平移\(114514\)格。

最后一问！函数\(y=a(x+h)^2+k\)和\(y=ax^2\)呢……

哦！原来顶点式的本质就是平移！原来的\(y=ax^2\)顶点是\((0,0)\)，向左平移\(h\)格，向上平移\(k\)格就是顶点式！而且，由于顶点也按照这种方式平移，因而我们很快得出，其顶点为\((-h, k)\)。

再由于顶点式都可以被化为定义式：

\[y=a(x+h)^2+k=ax^2+2ahx+k \]

\[(a'=a, b'=2ah, c'=k) \]

因此得到一个惊人结论：

任意抛物线\(y=ax^2+bx+c(a\ne 0)\)，都可以由\(y=ax^2\)平移而来。平移方法我就不赘述了，先化成顶点式即可。

这也解答了上面的疑问，关于开口大小和开口方向的结论适用于任意抛物线。