时间复杂度大讲堂
引入
观察以下两段代码。
int cnt = 0;
for(int i = 1; i <= n; ++i)
if(i % 2 == 0)
++cnt;
cout << cnt << endl;
cout << n / 2 << endl;
它们实现的功能其实相同,就是找出区间\([1, n]\)内偶数的个数。哪一个更简单呢?
显然是第二个。
理由是,第一段程序需要把\(1\)到\(n\)的所有整数遍历一遍,需要一定的时间,而第二段程序只要执行一个算术运算即可。这种差距在\(n\)增长到很大时更加明显。
为了表示一种算法的运行效率,即算法运行时间随算法中输入量的增大而增长的速率,我们定义了时间复杂度(\(Time\ Complexity\))。
必须要明确的是,时间复杂度描述的是算法随输入量增长的速度,与硬件的性能无关。有的同学可能会有这样的误解,就是只要我配个最新版\(5090Ti\)显卡加强劲的\(GPU\)(图形处理器)和英特尔\(i9\)的十代\(CPU\)(中央处理器),就可以把\(10^{10}\)次循环压在\(1s\)内完成,时间复杂度肯定低到爆炸吧!
这种理解有一个根本性问题,就是没有搞懂时间复杂度的定义。时间复杂度和硬件处理算法的时间,半毛钱关系都没有。我们可以把硬件处理算法的时间和输入量看成函数关系,那么这个函数的增长速率(导数?严格上不算是)就可以看成时间复杂度。这样定义的好处在于,好的硬件,即使是超级计算机,只能把运行时间缩短,随着输入量不断增大,增长速率最终会趋向于一个特定的值,这个值是该算法的属性,即时间复杂度。可以结合下图加以理解。
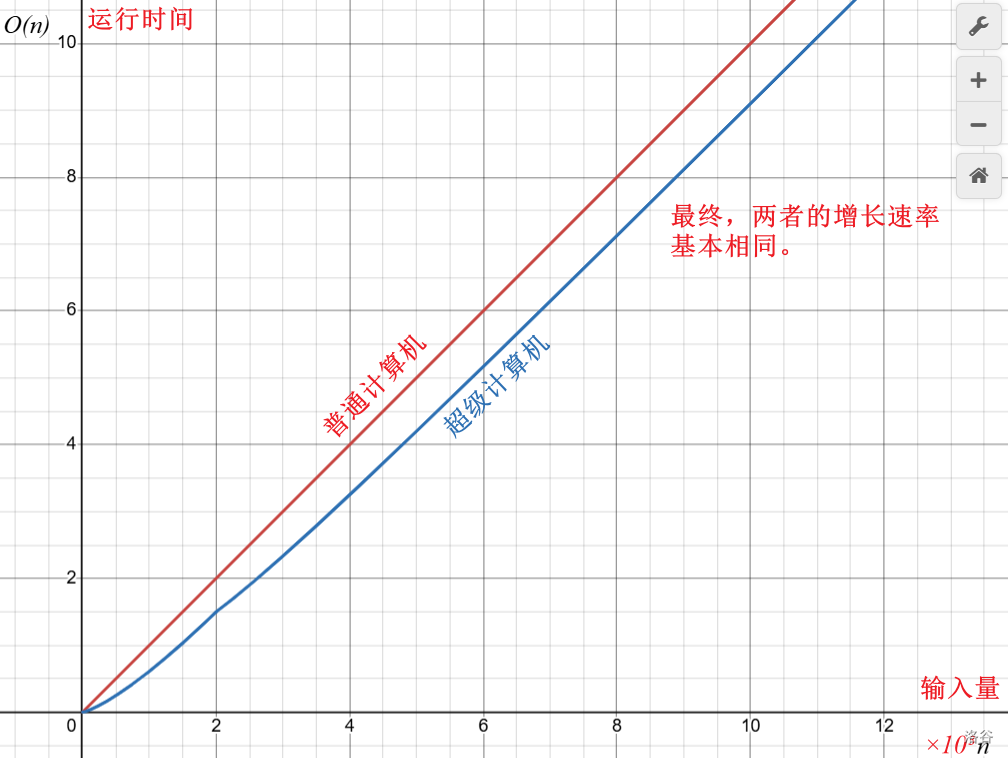
大\(O\)表示法
声明:初学时,时间复杂度可以简化为算法的运算次数随输入量的增长速率。
既然我们已经定义了时间复杂度,就需要把复杂度量化。那么,如何量化呢?我们定义了大\(O\)表示法。
再次观察下面的代码。
cout << n / 2 << endl;
对于这段代码,是不是对于任何的输入\(n\),都不需要执行任何循环?我们可以说,不论\(n\)取何值,它只需要执行一次运算,因此它的复杂度可以定为\(1\)。为了标识它是一个时间复杂度,我们把它用括号括起来,并在前面加上一个大\(O\),变成:
这就是大\(O\)表示法。
那我们看下优化之前的代码,时间复杂度是多少呢?
int cnt = 0;
for(int i = 1; i <= n; ++i)
if(i % 2 == 0)
++cnt;
cout << cnt << endl;
可以发现,该算法每次运行,需要执行\(\frac n 2\)次自增操作,那它的时间复杂度就是……\(O(\frac n 2)\)?
我们规定,在时间复杂度的大\(O\)括号中,对于每个未知输入量,只保留最高次项。最高次项的系数一律舍去。
这样做的初衷其实是为了让时间复杂度的表达更加简洁。毕竟,没有人希望自己算法的复杂度是\(O(\frac {243\sqrt 3} 3n^2+\sum_{i=1}^{n} \frac {\sqrt i} {114514}n)\)吧!因此,上述算法的时间复杂度写成:
舍系数的规定虽然在绝大多数情况下没有对时间复杂度造成多大影响,但是某些情况下,如果未知输入量前的常数系数太大,舍去可能会适得其反。最著名的是链式哈希算法\(unordered\ map\),由于常数系数是天文大数,因此有些时候还不如时间复杂度略逊一筹的红黑树算法\(map\)。
常见的算法时间复杂度
观察以下代码。
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= i; ++j)
++cnt;
代码的时间复杂度是多少?
外层循环走一遍,内层循环跑断腿。
容易发现,\(i=1\)时,\(j∈[1, 1]\);\(i=2\)时,\(j∈[1, 2]\);\(i=3\)时,\(j∈[1, 3]\)……\(i=n\)时,\(j∈[1, n]\)。也就是说,对于\(i\)从\(1\)遍历到\(n\),内层的\(j\)都需要对应执行\(i\)遍自增操作,即分别执行\(1,2,3,\dots ,n\)次自增操作。
因此,其时间复杂度为:
运用高斯同学的求和公式,有:
展开:
保留最高次项:
舍去系数:
直至目前,我们已经集齐了三种复杂度,即\(O(1),O(n)\)和\(O(n^2)\)。当然,复杂度肯定不止三种,基本上可以分为以下几个:
| 时间复杂度 | 别称 | 常见算法 |
|---|---|---|
| \(O(1)\) | 常数时间复杂度 | 简单数学 |
| \(O(\log n)\) | 对数时间复杂度 | 二分查找、求最大公因数 |
| \(O(\sqrt n)\) | 根号时间复杂度 | 分解质因数 |
| \(O(n)\) | 线性时间复杂度 | 欧拉筛、斐波那契数列(递推或记忆化递归) |
| \(O(n\log n)\) | — | 基于分治思想的排序算法 |
| \(O(n\sqrt n)\) | — | 对\([1, n]\)内整数分解质因数 |
| \(O(n^2)\) | 二次时间复杂度 | 背包问题、二维动态规划递推 |
| \(O(n^2\log n)\) | — | 每次输入都对现有的数进行归并排序 |
| \(O(n^3)\) | 三(高)次时间复杂度 | \(Floyd\)最短路算法 |
| \(O(2^n)\) | 指数时间复杂度 | 斐波那契数列(非记忆化的粗略估算) |
| \(O(\phi^n), \phi=\frac {\sqrt 5-1} 2\) | 黄金指数时间复杂度 | 斐波那契数列(非记忆化) |
| \(O(n!)\) | 阶乘时间复杂度 | 全排列 |
实际生活中,一个算法的时间复杂度越高,对硬件处理能力的要求也就越高。如果不选择提升性能,那就只能提升用户的耐心了。
现在很多题目都要求各位在\(1000ms\)内结束执行程序,可能有些人会说,\(1s\)的限制是不是显得太短了?毕竟我平时上的网站或者应用,也没有在\(1s\)内就结束加载啊?
曾经看到过一本书,是讲解\(Python\)的,为什么在这里提到呢?
书中有一段话,是这么讲的:\(Python\)是解释型语言,也就是说,在运行时需要一句一句翻译成机器语言,然后给计算机直接读取。编译型语言先通过编译器将源代码转换为可执行文件(\(Executable\ File\),缩写\(exe\)由此而来),这样运行时直接把“母语”喂给计算机,执行起来自然比解释型语言更快。最典型的例子就是\(C/C++\)。
但是,各位想想,假如一个算法,给\(C++\)运行,只需要\(1ms\);给\(Python\)边解释边运行,需要\(100ms\)。这里差距确实拉开了\(100\)倍,但是网速更慢,拖了用户\(3s\)……
我们发现,影响用户等待时间的,\(99\%\)都是网速。为什么?
我学过一些有关服务器的知识,因此可以知道,用最简单的获取版本信息举例,简化来讲,需要以下几个步骤:
- 客户端(\(Client\))给服务端(\(Server\))发送一个\(get\)请求(\(request\)),上面写好,需要获取游戏版本信息,客户\(IP\)地址,用户名等等。
- 快递员(互联网)收到请求,开始配送。找到服务端\(IP\)以后,把快递精准投送到服务器。
- 服务器发现了请求,首先验证身份。谁知道你这个\(IP\)是不是真的?包括但不限于,用户哈希,公密钥非对称加密等等。经过一番流程,确定你不是人机,开始提供服务。把版本信息打包好,传回一个响应(\(response\))。
- 快递员收到响应,递回客户端。在递回的过程中,快递员一不小心搞丢了一位(\(bit\))的数值,但它自己也没发现。但是,客户端这里如果直接拿损坏的数据作运算,是会出问题的。所以,这里加入了条件判断,判断这是不是一个损坏了的数据。数据损坏,也就是俗称的丢包,“包”是“数据包”的意思。数据损坏了怎么办呢?就需要重新向云端发送请求校验数据。这个过程需要继续,直到传输来的是一个正确的数据。
每一个请求的时间小于\(0.1s\),这还是在网速快、延迟低的情况下。加载一个游戏开始界面,可能需要发送成百上千的请求,虽然是异步处理的(就是说,一个请求若没有结束或发生异常,不会影响其它请求的收发与处理),但是加起来也需要\(5\)到\(10s\)的时间。有名的《蔚蓝档案》游戏开始界面加载,在模拟器端甚至要近\(1\)分钟。
既然网速已经很慢了,算法这块就不能再拖后腿了。对于一个游戏在一秒内扑面涌来的几千多万数据,必须在一秒内处理完,否则只能越积越多,就会造成卡顿,十分影响体验。因此,人们在算法优化的道路上越走越远,才取得了如今的辉煌成就。
以下是一些常见算法的时间复杂度,需要记忆:
| 算法 | 时间复杂度 |
|---|---|
| 冒泡排序 | 最好, 最坏, 平均:\(O(n),O(n^2),O(n^2)\) |
| 插入排序 | 最好, 最坏, 平均:\(O(n),O(n^2),O(n^2)\) |
| 选择排序 | 最好, 最坏, 平均:\(O(n^2)\) |
| 快速排序 | 最好, 最坏, 平均:\(O(n\log n),O(n^2),O(n\log n)\) |
| 归并排序 | 最好, 最坏, 平均:\(O(n\log n)\) |
| 堆排序 | 最好, 最坏, 平均:\(O(n\log n)\) |
| 桶排序 | 最好, 最坏, 平均:\(O(n+k),O(n^2),O(n+k)\) |
| 计数排序 | 最好, 最坏, 平均:\(O(n+k)\) |
| 基数排序 | 最好, 最坏, 平均:\(O(nk)\) |
| 希尔排序 | 最好, 最坏, 平均:\(O(n\log n),O(n^2),O(n\log n)\) |
| 二分查找 | \(O(\log n)\), 最坏情况\(O(n)\) |
| 插值查找 | 最好, 最坏, 平均:\(O(1),O(n),O(\log \log n)\) |
| 二叉搜索树 | \(O(\log n)\), 最坏情况\(O(n)\) |
| 分块 | \(O(\sqrt n)\) |
| 深度优先搜索(\(DFS\))和广度优先搜索(\(BFS\)) | \(O(V+E)\) |
| 迪杰斯特拉(\(Dijkstra\)) | 稠密图, 稀疏图:\(O(V^2), O((V+E)\log V)\) |
| \(A*\) | 取决于启发函数的选择,但一般低于\(Dijkstra\)。 |
| 贝尔曼·福特(\(Bellman-Ford\)) | \(O(VE)\) |
| 弗洛伊德(\(Floyd\)) | \(O(V^3)\) |
| 它死了(\(SPFA\)) | \(O(kE), k≈2\), 最坏情况\(O(VE)\) |
| \(Prim\)(朴素) | \(O(V^2)\) |
| \(Prim\)(堆优化) | \(O(E\log V)\) |
| \(Kruskal\)(并查集优化) | \(O(E\log E)\) |
| 试除法筛质数(朴素) | \(O(n^2)\) |
| 试除法筛质数(简单数学优化) | \(O(n\sqrt n)\) |
| 埃拉托斯特尼筛法(埃筛) | \(O(n\ln \ln n)\) |
| 线性筛法(欧(拉)筛) | \(O(n)\) |
| 快速幂 | \(O(\log n)\) |
| 最大公约数算法\(\gcd\)或扩展欧几里得算法\(Ex-\gcd\) | \(O(\log(\min(a, b)))\) |
| 分解质因数 | \(O(\sqrt n)\) |
| 欧拉函数\(\phi(n)\) | \(O(\sqrt n)\) |
| 求\([1,n]\)所有整数的欧拉函数(朴素) | \(O(n\sqrt n)\) |
| 求\([1,n]\)所有整数的欧拉函数(欧筛优化) | \(O(n)\) |
| 莫比乌斯函数\(\mu(n)\) | \(O(\sqrt n)\) |
| 中国剩余定理(\(CRT\)) | \(O(k\log M)\) |
| 全排列 | \(O(n!)\) |
| 斐波那契数列(非记忆化) | \(O(\phi^n)\), 粗略估计\(O(2^n)\) |
| 斐波那契数列(记忆化递归或递推) | \(O(n)\) |
| 一维动态规划问题(如爬楼梯) | \(O(n)\) |
| 最长上升子序列(或最长不降子序列, 朴素) | \(O(n^2)\) |
| 最长上升子序列(或最长不降子序列, 二分优化) | \(O(n\log n)\) |
| 背包 | 通常是\(O(nW)\) |
| 最长公共子序列 | \(O(mn)\) |
| 线段树 | 创建\(O(\log n)\), 操作\(O(\log n)\) |
| 树状数组 | \(O(\log n)\) |
| 简单前缀和 | 创建\(O(n)\),询问\(O(1)\) |
| 简单差分 | 创建\(O(n)\),区间修改\(O(1)\) |
| \(k\)维前缀和(\(k∈N^+且k\geq 1\)) | 创建\(O(n^k)\),询问\(O(1)\) |
| \(k\)维差分(\(k∈N^+且k\geq 1\)) | 创建\(O(n^k)\),区间修改\(O(1)\) |
| \(ST\)表 | \(O(\log n)\) |
求解递推方程
求递推式的时间复杂度。
\[T(n)=T(n-1)+n, 其中T(1)=1 \]
之前都是通过代码和特定算法判断时间复杂度,这次,终于是理论计算的时候了!
观察该方程。
这似乎是一个递推关系式(递归函数),每一项的值与且仅与前一项有关联,且前一项是一个未知数。因此,我们必须消去前一项,而这样就必须代入消元。
未知数还没消完:
重复以上过程,直到:
这样才算是真正消除了未知数。运用求和公式,有:
写成时间复杂度,即可得:
这就是通过递推式求时间复杂度,也就是行业黑话“求解递推方程”。不过,对于第一步,我们整理一下格式,可以写成:
这样看起来可能整洁优雅一些。
练习:
求解递推方程\(T(n)=T(n-1)+1\),其中\(T(1)=1\)。
解:
第一步:展开递推式。\[\because T(n)=T(n-1)+1 \]\[T(n-1)=T(n-2)+1 \]\[\dots \]\[T(3)=T(2)+1 \]\[T(2)=T(1)+1 \]\[T(1)=1 \]\[\therefore 将所有上式相加,得: \]\[\sum_{i=1}^nT(i)=\sum_{i=1}^{n-1}T(i)+\sum_{i=1}^n 1 \]\[两边同时减去\sum_{i=1}^{n-1}T(i): \]\[T(n)=\sum_{i=1}^n 1=n \]写成时间复杂度,即得:
\[T(n)=O(n) \]经过验算,由于该递推式需要从\(n\)推到\(1\),因此至少有\(O(n)\)的复杂度,我们的运算是正确的。
求解递推方程:
\[T(n)=T(\frac n 2)+n, 其中T(1)=1 \]注:\(\lfloor \frac n 2\rfloor\)以后通作为\(\frac n 2\)。
老套路了属于是,先展开递推式:
上式的左右分别相加,得到:
至于为什么是\(\log n\),是因为\(\frac n {2^i}_{min}=1\),所以\(2^i_{max}=n\),所以\(i_{max}=\log_2n\)即\(\log n\)。
到这一步似乎没法推进了,但是让我们把求和式展开:
哎,这不是那什么等比数列求和吗?上公式!
代入\(q=2\),\(a_1=1\),则有:
需要注意的是,这里的\(n\)指项数,而显然该数列有\(\log n+1\)项。
根据对数的定义,有:
牢谦复杂度第一定理
我们考虑一种普遍情况,即递推方程\(T(n)=T(\frac n 2)+an+b\)。其中\(a,b\)是常数。
照样展开递推式:
相加相消,有:
代入\(a_1=a\),\(q=2\),有:
其中,\(1, b\)和\(-a\)是常数项,\(b\log n\)是对数项(次幂显然比一次项低),\(2an\)是一次项,根据保留最高次项和舍系数的原则,我们得出了该类递推方程式的通解,即\(T(n)=O(n)\)。
牢谦复杂度第一定理
对于一个具有如下形式的递推方程:
\[T(n)=T(\frac n 2)+an+b, 其中a,b是常数 \]其通解为:
\[T(n)=O(n) \]
普遍の规律
考虑二次递推方程\(T(n)=T(\frac n 2)+an^2+bn+c\),其中\(a,b,c\)是常数。
展开递推式:
相加相消:
等比数列求和:
保留最高次项:
对于一个三次递推方程\(T(n)=T(\frac n 2)+an^3+bn^2+cn+d\),其中\(a,b,c,d\)是常数,它有通解吗?若有,请求出;若没有,请说明理由。
留作课后习题。
参考答案:
展开递推式:
\[T(n)=T(\frac n 2)+an^3+bn^2+cn+d \]\[T(\frac n 2)=T(\frac n 4)+\frac {an^3} 8+\frac {bn^2} 4+\frac {cn} 2+d \]\[\dots \]\[T(2)=T(1)+8a+4b+2c+d \]\[T(1)=a+b+c+d \]相加相消:
\[T(n)=\sum_{i=0}^{\log n}(8^ia+4^ib+2^ic+d) \](这样写是不是更好看一些?)
等比数列求和:\[T(n)=\frac {a(8^{\log n+1}-1)} {8-1}+\frac {b(4^{\log n+1}-1)} {4-1}+\frac {c(2^{\log n+1}-1)} {2-1}+d(\log n+1) \]\[T(n)=\frac 8 7an^3-\frac a 7+\frac 4 3bn^2-\frac b 3+2cn-c+d\log n+d \]设\(-\frac a 7-\frac b 3-c+d\)为常数\(C\),得:
\[T(n)=\frac 8 7an^3+\frac 4 3bn^2+2cn+d\log n+C \]\[T(n)=O(n^3) \]
你……有没有……发现某种规律?
牢谦复杂度第一定理推广式
牢谦复杂度第一定理推广式
对于一个具有如下形式的递推方程:
\[T(n)=T(\frac n 2)+a_0+a_1n+a_2n^2+a_3n^3+\dots+a_kn^k 其中[a_0,\dots,a_k]是常数 \]也可写成:
\[T(n)=T(\frac n 2)+f(n), 其中f(n)是递推过程中的运算 \]其通解为:
\[T(n)=O(n^k)或者T(n)=O(f(x)) \]
以下是简要证明:
展开递推式:
相加相消:
等比数列依次求和:
展开:
为便于记录,我们将所有常数项记为\(C_0\)。诸如\(2a_1, \frac {4a^2} 3, \dots,\frac {2^ka_k} {2^k-1}\)的系数,根据其所在项的次幂,依次记作\(C_1,C_2,\dots,C_k\),则有:
一目了然!常数项、对数项、一次项……\(k\)次项,极目望去,小学二年级同学也可知道:
牢谦复杂度第一定理推广式,证毕。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号