一元二次方程全套教程一命速通

文化水平：初二。
文章是一元二次方程概念性知识速通版。请不要盲目模仿文章中的格式。

一元二次方程的定义

一个正方形的面积是\(5\)，请列方程求出边长。
我国两年内总人口从\(139538\)万人增长到\(141177\)万人，请列方程求出年平均增长率。
在循环赛中，\(x\)个球队总计赛\(36\)场，求\(x\)。

以上这些实际问题分别列方程为：

\[x^2=5 \]

\[1395380000(1+x)^2=1411770000 \]

\[\frac {x(x-1)} 2=36 \]

这些方程都有一个共同点：展开后，\(x\)的最高次为\(2\)。

我们定义，只含有一个未知数，并且未知数的最高次数是2的方程叫做一元二次方程（quadratic equation with one unknown）。

一元二次方程的一般形式是\(ax^2+bx+c=0(a\neq 0)\)。其中，\(ax^2\)、\(bx\)和\(c\)分别叫做二次项、一次项和常数项，\(a\)、\(b\)分别叫做二次项系数、一次项系数。

一元二次方程的解应该写成\(x_1=a, x_2=b\)的形式。

一元二次方程的解法

一元二次方程我哪会解啊。我只会解一元一次方程。

直接开平方法

解方程：

\[x^2=9 \]

Hmm...我希望把一元二次方程转化为一元一次方程，那我就利用算术平方根进行降次。

\[x=±\sqrt 9=±3 \]

\[x_1=3, x_2=-3 \]

简单😎。那么类比我们可以通过直接开方解出以下类型的方程：

\[x^2=k \]

\[x^2+h=k \]

\[(x+h)^2=k \]

\[(x+h)^2+p=k \]

练习

用直接开平方法解以下方程：

\[(1)x^2=9 \]

\[(2)x^2+1=\frac {13} 4 \]

\[(3)(x+2)^2=5 \]

\[(4)x^2+8=\frac {31}{4} \]

配方法

解方程：

\[x^2-4x+3=0 \]

啊，直接开平方法这不炸了吗，连开方都开不了。
那就配出【一个】平方。

\[x^2-4x+4=1 \]

\[(x-2)^2=1 \]

然后利用直接开平方法即可。

\[x-2=±1 \]

\[x_1=3, x_2=1 \]

这是二次项系数为\(1\)的配方法，那如果二次项系数不为\(1\)呢？

\[2x^2+x-3=0 \]

没事，让我们转化一下。

\[x^2+\frac 1 2x-\frac 3 2=0 \]

\[x^2+2\cdot \frac 1 4x+\frac 1 {16}=\frac {25}{16} \]

\[(x+\frac 1 4)^2=\frac {25}{16} \]

\[x+\frac 1 4=±\frac 5 4 \]

\[x_1=1, x_2=-\frac 3 2 \]

这就是系数不为\(1\)的配方法。

哎，你看，既然我们具体数字的配方法会了，那么把数字换成字母，你没有理由不会了吧！
解方程：

\[x^2+px+q=0 \]

哎呀，这不就是基本操作嘛！配方上！

\[x^2+px+\frac {p^2} 4=\frac {p^2} 4-q \]

\[(x+\frac p 2)^2=\frac {p^2-4q} 4 \]

\[x+\frac p 2=±\frac {\sqrt {p^2-4q}} 2 \]

\[x_1=\frac {-p+\sqrt {p^2-4q}} 2,x_2=\frac {-p-\sqrt {p^2-4q}} 2 \]

哎？怎么错了？
哦，原来\(p^2-4q\)没说一定要大于等于\(0\)。

\[①p^2-4q>0: x_1=\frac {-p+\sqrt {p^2-4q}} 2,x_2=\frac {-p-\sqrt {p^2-4q}} 2 \]

\[②p^2-4q=0: x_1=x_2=-\frac p 2 \]

\[③p^2-4q<0: 方程没有实数根 \]

这提醒我们，以后一定要注意分情况讨论。
其实这里算出来的\(x_1\)和\(x_2\)，就是求根公式的变形。

配方法的几何意义

让我们移步到《周髀算经》，看看我们的赵爽同学是如何解形如\(x^2+px=q\)的一元二次方程的。
容易发现，任意一个一元二次方程都可以化为\(x^2+px=q\)的形式。
众所周知，古时候的人们在认识数学时，都是从生活中得到的灵感，因此他们在思想上自然地排除掉了负数的一种情况。于是赵爽同学只研究了\(x\geq0\)的一种情况，这是因古时人们的思考方式决定的，我们也不能说他错。毕竟几何上基本是没有负数一说的。

首先赵爽将方程变形为：

\[x(x+p)=q \]

这一步的几何意义是构造一个长方形，其一边是\(x\)，另一边是\(x+p\)，而面积是\(q\)。

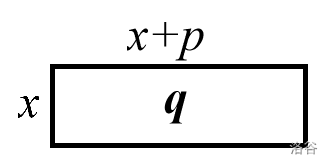
接下来，赵爽发动传统艺能勾股弦图，复制粘贴了四份，并按照弦图的方法拼起来。

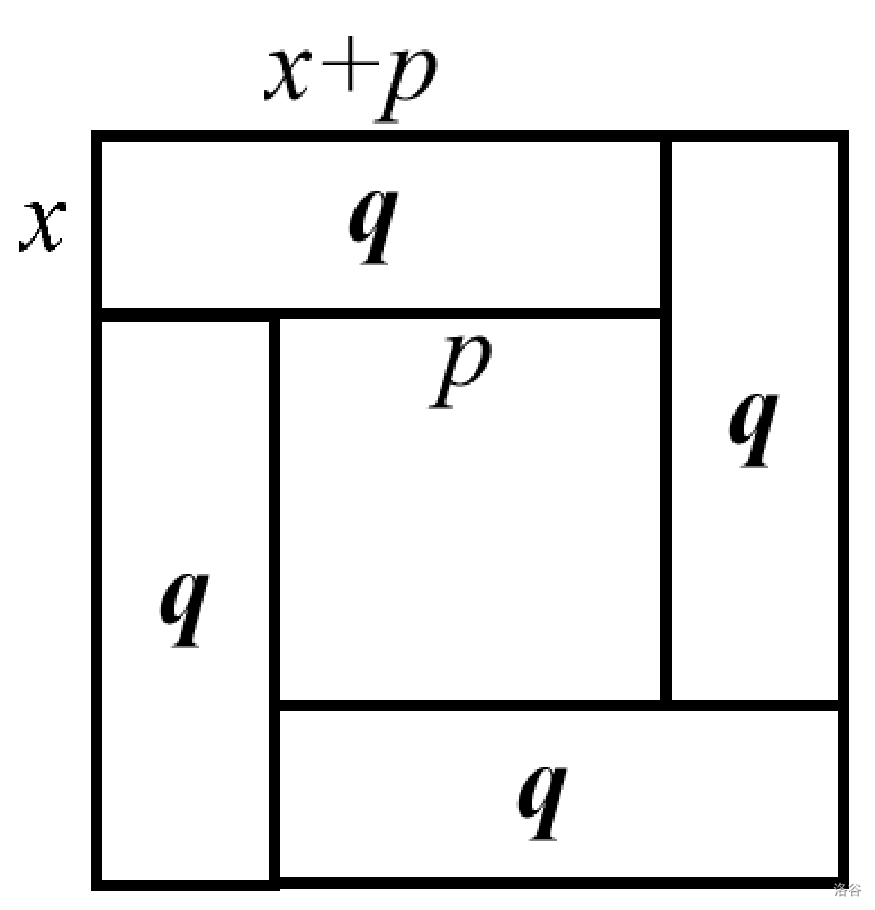
赵爽惊奇地发现，拼成的正方形面积等于\((x+x+p)^2\)，而同时又等于四个长方形加一个正方形，即\(p^2+4q\)，因此容易有：

\[(2x+p)^2=p^2+4q \]

我们开方的过程，相当于在求正方形的边长。

\[2x+p=\sqrt {p^2+4q} \]

成功地完成了降次。

赵爽同学最终推出来的“求根公式”是：

\[x=\frac {-p+\sqrt {p^2+4q}} 2 \]

在不考虑负数的情况下，该公式完全正确。因为我们刚刚考虑的是\(x^2+px+q=0\)，和赵爽的原方程中\(q\)构成相反数，因此此处是\(p^2+4q\)。
有的人就要叫起来了，哎主播主播，他没有考虑根号下小于\(0\)！
首先，在几何方面解释，一个正方形的面积怎么可能是负数呢？不用考虑。另外，赵爽同学默认了\(q\geq0\)，因此可推出\(p^2+4q\geq0\)，到头来还是因为古代不接受负数。

课本上利用了不同的几何方法，大家可以自行研究。

练习

用配方法解以下方程：

\[(1)x^2 + 5x + 6 = 0 \]

\[(2)x^2 - \frac 3 2x - 1 = 0 \]

\[(3)2x^2+ 12x - 14 = 0 \]

\[(4)3x^2 - 9x + 6 = 0 \]

公式法

有的同学说，主播主播，这个配方法还是太吃操作了，还十分的繁琐。有没有什么简单（无脑）又强势（迪奥）的方法推荐一下呢？
有的兄弟，有的。让我们把配方法里面的数字用字母表示，然后推算一遍。

\[ax^2+bx+c=0(a\neq 0) \]

因为\(a\neq 0\)，所以两边同除以\(a\)：

\[x^2+\frac b ax+\frac c a=0 \]

仿照二次项系数为\(1\)的配方法进行配方：

\[x^2+2\cdot \frac b {2a}x+\frac {b^2}{4a^2}=\frac {b^2}{4a^2}-\frac c a \]

\[(x+\frac b {2a})^2=\frac {b^2-4ac} {4a^2} \]

方程化为了\((x+h)^2=k\)的形式。首先应判断\(\frac {b^2-4ac} {4a^2}\)的正负。

\[\because a\neq 0\therefore 4a^2>0 \]

方程若有解，即\(\frac {b^2-4ac} {4a^2}\geq0\)，因此只能有\(b^2-4ac\geq 0\)。

\[当b^2-4ac\geq 0时， \]

\[x+\frac b {2a}=\frac {±\sqrt {b^2-4ac}} {2a} \]

\[x_1=\frac {-b+\sqrt {b^2-4ac}} {2a}, x_2=\frac {-b-\sqrt {b^2-4ac}} {2a} \]

你发现，一元二次方程\(ax^2+bx+c=0(a\neq 0)\)的根是由方程的各系数\(a, b,c\)确定的。当\(b^2-4ac\geq0\)时，它的实数根是：

\[x=\frac {-b±\sqrt {b^2-4ac}} {2a} \]

有的同学要叫起来了。
这是求根公式——最纯粹的力量。直接套用求根公式得到一元二次方程实数根的方法被称作公式法。

从求根公式中，你可以看出一元二次方程实数根的个数和什么有关吗？

你发现，根号下的\(b^2-4ac\)是重点。当它大于\(0\)时，\(±\sqrt {b^2-4ac}\)可以开出两个实数；当它等于\(0\)时，\(±\sqrt {b^2-4ac}\)只能开出一个\(0\)；当它小于\(0\)时，根号无意义。

因此，我们容易得出：

\(b^2-4ac\)	解的情况
\(>0\)	有两个不相等的实数根
\(=0\)	有两个相等的实数根
\(<0\)	没有实数根

这个时候有的同学又要叫起来了。
我们定义，\(b^2-4ac\)是一元二次方程\(ax^2+bx+c=0(a\neq 0)\)的根的判别式，记为\(\Delta\)。

备注：在新版教材里，不强调\(\Delta\)。请不要在练习中出现这个“三角形”。

“双圈”问题

已知关于\(x\)的一元二次方程\(ax^2-2x+1=0\)有两个不相等的实数根，求\(a\)的取值范围。

第一次做这道题目的你：

\[b^2-4ac=4-4a>0 \]

\[a<1 \]

哎？怎么错了？
卧槽，原来是一元二次方程，有\(a\neq0\)。

已知关于\(x\)的方程\(ax^2-6x+5=0\)有实数根，求\(a\)的取值范围。

这下真的看清楚了。

\[\left\{ \begin{aligned} &b^2-4ac=36-20a\geq 0 \\ &a\neq 0\\ \end{aligned} \right.\]

\[a\leq \frac 9 5且a\neq 0 \]

又错了？
哦，原来这次是方程。\(a\leq \frac 9 5\)。

这样的题目，我们称为“双圈问题”。以下是一些双圈问题的条件搭配：

对于方程\(ax^2+bx+c=0\)：

		\(A\)	\(B\)
		一元二次方程	方程
\(1\)	有两个不相等的实数根	\(a\neq 0且b^2-4ac>0\)	见\(A1\)
\(2\)	有两个相等的实数根	\(a\neq 0且b^2-4ac=0\)	见\(A2\)
\(3\)	有两个实数根	\(a\neq 0且b^2-4ac\geq0\)	见\(A3\)
\(4\)	有实数根	\(b^2-4ac\geq0且a\neq0\)	\(\left\{\begin{aligned}&a=0&b\neq 0或b=0且c=0\\&a\neq 0&b^2-4ac\geq0\\\end{aligned}\right.\)
\(5\)	没有实数根	\(b^2-4ac<0\)	\(\left\{\begin{aligned}&a=0&b=0且c\neq 0\\&a\neq 0&b^2-4ac<0\\\end{aligned}\right.\)

这里面的规律，读者自证不难。不过，让我们复习一下：

解方程：

\[ax=b \]

答案：

\[\left\{\begin{aligned}&a\neq0&x=\frac b a\\&a=0&\left\{\begin{aligned}&b=0&x取全体实数\\&b\neq 0&x无解\\\end{aligned}\right.\\\end{aligned}\right. \]

提示：“双圈问题”在解答题中一般分值较高。请注意该类题型的格式与技巧。

练习

$1. $用公式法解以下方程：

\[(1)x^2+4x-5=0 \]

\[(2)3x^2-x-2=0 \]

\[(3)-2x^2+2\sqrt 2x+1=0 \]

$2. $不解方程，判别方程根的情况：

\[(1)x^2+3x-1=0 \]

\[(2)2y^2-3y+4=0 \]

\[(3)x^2+5=2\sqrt 5x \]

因式分解法

解方程：

\[x^2-x=0 \]

左边因式分解：

\[x(x-1)=0 \]

可得两个一次方程：

\[x=0\ \ \ \ \ \ \ (1)\ \ \ x-1=0\ \ \ \ \ \ \ (2) \]

解得：

\[x_1=0, x_2=1 \]

因式分解法，无师自通。
仅适用于左边可以因式分解的一元二次方程。

练习

用因式分解法解以下方程：

\[(1)x^2+6x=0 \]

\[(2)9t^2-(t-1)^2=0 \]

\[(3)25x^2-5x+\frac 1 4=0 \]

\[(4)(x+1)^2+8x+24=0 \]

备注：在实际应用中，没有要求一定要用哪种方法解方程，你可以选择合适的方法解方程。常用的顺序是：

因式分解法→公式法→配方法（被世界遗忘）
直接开平方法只在特殊情况下能用。

一元二次方程的根与系数的关系（韦达定理）

观察下列方程：

方程	\(x_1\)	\(x_2\)
\(x^2-5x+4=0\)	\(1\)	\(4\)
\(x^2+5x+6=0\)	\(-2\)	\(-3\)
\(x^2+7x-8=0\)	\(1\)	\(-8\)
\(2x^2+7x-4=0\)	\(\frac 1 2\)	\(-4\)
\(2x^2-9x+7=0\)	\(1\)	\(\frac 7 2\)

观察这两个根与系数\(a,b,c\)之间有什么关系？

经过尝试，我们惊奇的发现对于一元二次方程\(ax^2+bx+c=0\)，若有两个实数根\(x_1, x_2\)，则两根的和似乎都等于\(-\frac b a\)，两根的积都等于\(\frac ca\)。
能否进行验证呢？很简单，掏出我们最纯粹的力量。

\[已知对于方程ax^2+bx+c=0(b^2-4ac \geq0且a\neq 0)， \]

\[其两根分别为x_1=\frac {-b+\sqrt {b^2-4ac}} {2a}, x_2=\frac {-b-\sqrt {b^2-4ac}} {2a} \]

\[x_1+x_2=\frac {-b+\sqrt {b^2-4ac}-b-\sqrt {b^2-4ac}} {2a}=-\frac b a \]

\[x_1x_2=\frac {(-b)^2-(\sqrt {b^2-4ac})^2} {4a^2}=\frac {b^2-b^2+4ac} {4a^2}=\frac c a \]

证毕。

这个神奇的定理被称作韦达定理。

这个结论在求两根和与积、已知一根求另一根或者由根反推方程式时十分好用。韦达定理的有关题目并没有什么难度，我们简单归纳一下：一种大题和一种小题。

证明大题

已知关于\(x\)的一元二次方程\(x^2+(m+3)x+m+1=0\)。
\((1)\)求证：无论\(m\)取何值，原方程总有两个不相等的实数根；
\((2)\)若\(x_1\)、\(x_2\)是原方程的两根，且\(|x_1-x_2|=2\sqrt 2\)，求\(m\)的值。

这就是韦达定理唯一解答题考法：证明实数根\(+\)利用定理计算。接下来把解法讲解一下。

\((1)\)证明：

\[a=1, b = m+3, c = m+1 \]

\[b^2-4ac=(m+3)^2-4(m+1)=m^2+2m+5=(m+1)^2+4 \]

\[\because(m+1)^2\geq 0, (m+1)^2+4>0 \]

\[\therefore b^2-4ac>0, 原方程总有两个不相等的实数根. \]

\((2)\)都出现在韦达定理里面了，总得用一下吧。

\[x_1+x_2=-\frac b a=-m-3, x_1x_2=\frac c a=m+1 \]

\[\because |x_1-x_2|=2\sqrt 2 \]

\[\therefore (x_1-x_2)^2=8 \]

\[\therefore (x_1+x_2)^2-4x_1x_2=8 \]

\[\therefore (m+3)^2-4(m+1)=8 \]

\[m^2+2m+5=8 \]

\[解得m_1=1, m_2=-3 \]

总之，第\((1)\)题很简单，第\((2)\)题先使用一次韦达定理，然后向“知二推二”和题目条件上硬凑即可。较为简单。

小题—没做过就做不出来系列

这种题目属于是没做过就怎么也做不出来，做过了不管怎么变换都能做出来的类型。下面举一个例子：

若\(ab\neq 1\)，且有\(5a^2+2024a+9=0\)及\(9b^2+2024b+5=0\)。则\(\frac a b\)的值是多少？

这是我当时使用的方法：

解：容易知道：

\[a=\frac {-2024±\sqrt {2024^2-4\cdot 5\cdot 9}} {10} \]

\[b=\frac {-2024±\sqrt {2024^2-4\cdot 5\cdot 9}} {18} \]

\[\therefore \frac a b=\frac {\frac {-2024±\sqrt {2024^2-4\cdot 5\cdot 9}} {10}} {\frac {-2024±\sqrt {2024^2-4\cdot 5\cdot 9}} {18}}=\frac {\frac 1 {10}} {\frac 1 {18}}=\frac 9 5 \]

但是，这个方法其实是有点问题的。\(a\)、\(b\)的正负号其实可以相反着取，这样上下两个分子就无法约去。但是，本题很巧的地方就在于：

\[\frac {-2024+\sqrt {2024^2-4\cdot 5\cdot 9}} {10}\cdot \frac {-2024-\sqrt {2024^2-4\cdot 5\cdot 9}} {18} \]

\[=\frac {(-2024)^2-(\sqrt {2024^2-4\cdot 5\cdot 9})^2} {180} \]

\[=\frac {2024^2-2024^2+4\cdot 5\cdot 9} {180} \]

\[=1 \]

与题目条件\(ab\neq 1\)不符。因此，\(\frac a b\)只可能是\(\frac 9 5\)。

刚刚是暴力解法，那么我们能否巧妙使用韦达定理求解呢？
对想出这种解法的人的注意力表示崇高的敬意。

我们注意到，\(\frac a b=a\cdot \frac 1 b\)，这启示我们使用韦达定理（两根之积）进行求解。
观察两个方程，发现其二次项和常数项系数恰好相反。因此容易想到，将方程\((2)\)两边同除以\(b^2\)：

\[9+2024\cdot\frac 1 b+5\cdot\frac 1 {b^2}=0 \]

将\(\frac 1 b\)看成整体，与方程\((1)\)联立：

\[\left\{\begin{aligned}5a^2&+2024a&+9=0\\5(\frac 1 b)^2&+2024(\frac 1 b)&+9=0\end{aligned}\right. \]

看出来了吗？我们可以把\(a\)和\(\frac 1 b\)看做同一方程的两个根，那么：

\[a\cdot \frac 1 b=\frac c a=\frac 9 5 \]

举一反三，触类旁通。

一元二次方程的应用

敬请期待……

拓展：“转化”的思想

回顾我们之前解方程的方法，其实都有一个共同点——转化。即，将未知的方程转化为已知解法的方程并解之。

\[一元一次方程\stackrel{去分母、去括号、移项、合并同类项、系数化为1}{\longrightarrow}x=a \]

\[二元一次方程\stackrel{代入消元、加减消元}{\longrightarrow}一元一次方程 \]

\[一元二次方程\stackrel{直接开平方法、配方法、公式法、因式分解法}{\longrightarrow}一元一次方程 \]

\[分式方程\stackrel{去分母}{\longrightarrow}整式方程+检验↑ \]

利用转化的思想，我们还可以解一些新的方程。

解一元三次方程：

\[x^3+x^2-2x=0 \]

\[x(x^2+x-2)=0 \]

\[x(x-1)(x+2)=0\ \ \ \ (因式分解法) \]

\[\therefore x_1=0, x_2=1, x_3=-2 \]

解无理方程（根号下含有未知数的方程）：

\[\sqrt {2x+3}+\sqrt {5x+1}=7 \]

两边平方：

\[2x+3+5x+1+2\sqrt {(2x+3)(5x+1)}=49 \]

孤立根号：

\[2\sqrt {(2x+3)(5x+1)}=-7x+45 \]

二次消根：

\[4(2x+3)(5x+1)=(-7x+45)^2 \]

化简：

\[9x^2-698x-2013=0 \]

公式法爆解，容易得到：

\[x_1=3, x_2=\frac {671} 9 \]

解无理方程在升次时会产生增根。

\[经检验，x_2=\frac {671} 9是增根； \]

\[原方程的解为x=3。 \]

题目汇编

$1. $【有理数之证】

已知关于\(x\)的一元二次方程\(ax^2+bx+c=0(a, b, c为有理数, a\neq 0)\)有一个根为\(4-\sqrt {13}\)，则它的另一个根是多少？为什么？

第一问一定很容易吧，答案是\(4+\sqrt {13}\)。
那么我们如何证明呢？这似乎是一道缺少条件的题目。但是，这里的有理数可以给我们一些提示。

同学的答案：

\[\because x_1=\frac {-b-\sqrt {b^2-4ac}} {2a}=4-\sqrt {13} \]

\[\therefore -\frac b {2a}=4, \frac {\sqrt {b^2-4ac}} {2a}=\sqrt {13} \]

\[\therefore x_2=\frac {-b+\sqrt {b^2-4ac}} {2a}=4+\sqrt {13} \]

嘿嘿，一分没有。
你可能会疑问，这样的证明过程难道不够严谨吗？
是的，而且从第二步开始就不严谨了。

我们需要从有理数的条件一步一步推出第二步的结论，并不是一下子就可以跳过来的。首先，我们回顾一下与有理数有关的一些基本定理。
请注意，以下描述中的\(∈Q\)，等效于\(是有理数\)。

1. 对于任意的\(a, b∈Q\)，有\(a+b, a-b, ab, \frac a b∈Q\)。
2. 存在\(a, b∉Q\)，使得\(a+b, a-b, ab, \frac a b中一项∈Q\)。
3. 对于任意的\(a+bk∈Q(a, b∈Q, k∉Q)\)，有\(b=0\)。
4. 对于任意的\(a∈Q, b∉Q\)，有\(a+b, a-b∉Q, \frac b a∉Q(a\neq 0)\)。
5. 存在\(a∈Q, b∉Q\)，使得\(ab, \frac a b∈Q\)。

第一项可以通过有理数的定义\(Q=\frac m n(m, n∈Z, n\neq 0)\)证明。

第二项可以举出反例：
\(a=4+\sqrt {13}, b=4-\sqrt {13}\)，满足\(a+b, ab∈Q\)。
\(a=b=4+\sqrt {13}\)，满足\(a-b, \frac a b∈Q\)。

第三、四项可以同理证明。

第五项可以举出反例，亦即\(a=0\)。

接下来我们开解。

因为条件有\(ax^2+bx+c=0\)有一根为\(x=4-\sqrt {13}\)，所以：

\[(4-\sqrt {13})^2a+(4-\sqrt {13})b+c=0 \]

\[29a-8\sqrt {13}a+4b-\sqrt {13}b+c=0 \]

因为我们抓住了有理数这一条件，所以要将有理数分离：

\[(29a+4b+c)-\sqrt {13}(8a+b)=0\ \ \ \ \ \ \ (1) \]

应用基本定理\(3\)：

\[8a+b=0 \]

代入式\((1)\)可得：

\[29a+4b+c=0 \]

当\(x=4+\sqrt {13}\)时，原方程：

\[\begin{aligned} 左边&=(4+\sqrt {13})^2a+(4+\sqrt {13})b+c \\ &=29a+8\sqrt {13}a+4b+\sqrt {13}b+c\\ &=(29a+4b+c)+\sqrt {13}(8a+b)\\ &=0+\sqrt {13}\cdot 0\\ &=0\\ 右边&=0 \end{aligned}\]

\[\therefore 左边=右边 \]

证毕。

这道题为我们与有理数相关的证明做出了一个很好的示范。