反比例函数进阶
现如今的出题老师已经不满足于考察单一的反比例函数了。他们乐于“合成”一些其它的函数,并要求你研究合成函数的性质。
对勾函数
定义
定义形如\(y=kx+\frac m x(k, m为常数且k, m\neq 0)\)的函数为对勾函数。
最简单的对勾函数是\(y=x+\frac 1 x\)。让我们先研究一下它吧。
图像
掏出几何画板方格纸,并按照“列表—描点—连线”的流程画出对勾函数的图像。
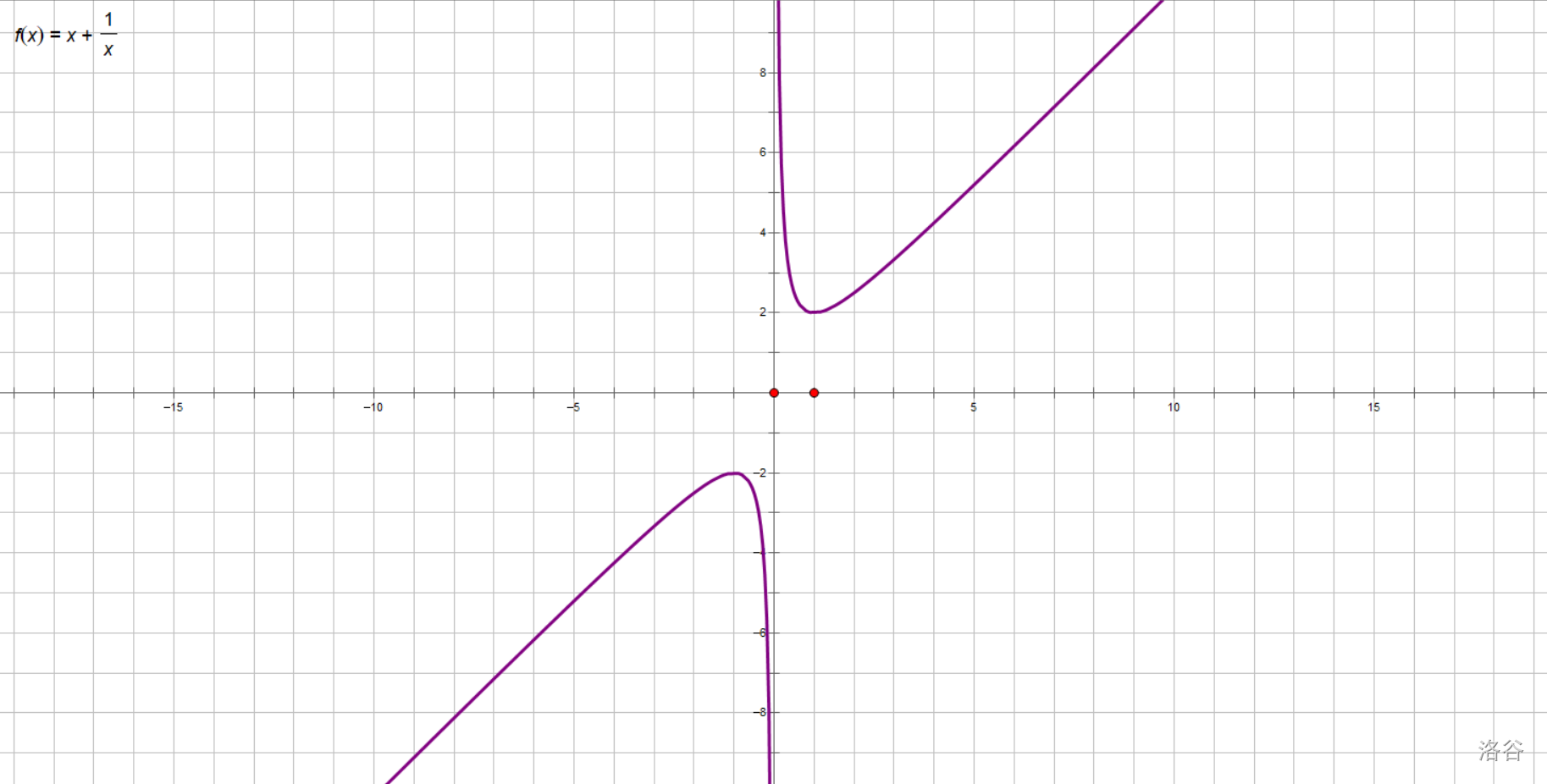
马上就晓得了,原来“对勾函数”的名字是这么来的啊。看!多像啊!

性质
增减性
对勾函数的增减性比较复杂。观察图像,发现它是一个双曲线,应该分两半进行探讨。
以\(x>0\)为例,\(x<0\)可同理证得。
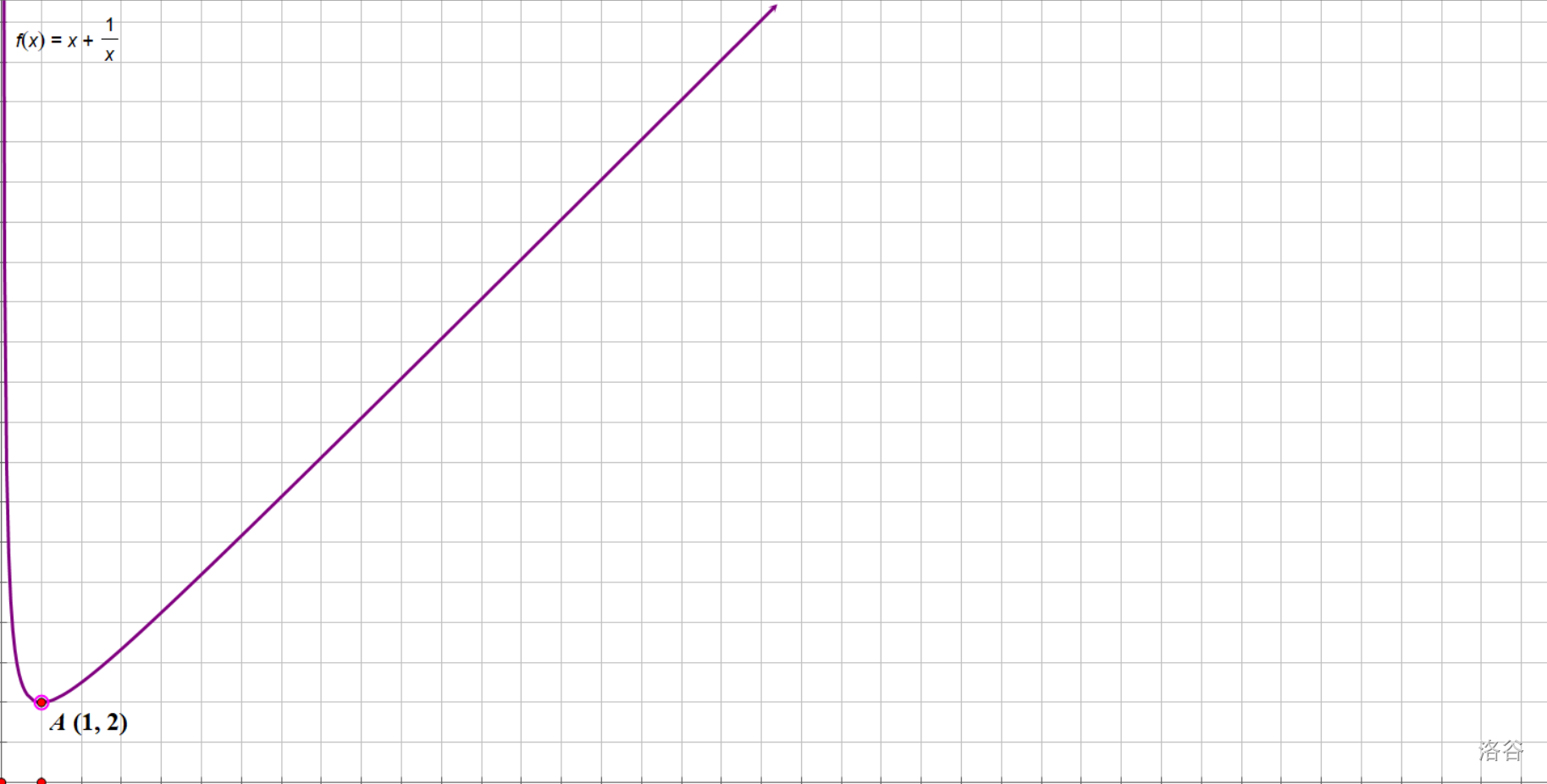
我们发现,图像在\(0<x<1\)时,\(y\)随\(x\)的增大而减小;\(x\geq 1\)时,\(y\)随\(x\)的增大而增大。
这是我们用“形”的方法看出来的。那如果用“数”的方法证明呢?
设函数\(y=x+\frac 1 x\)图像的正半支上存在两点\((a, a+\frac 1 a)\),\((b,b+\frac 1 b)\),且规定\(0<a<b\)。
作差法比大小:\[(b+\frac 1 b)-(a+\frac 1 a) \]\[=(b-a)+(\frac 1 b-\frac 1 a) \]\[=(b-a)+\frac {a-b}{ab} \]\[=\frac {(a-b)(1-ab)}{ab} \]易知\(ab>0, a-b<0\)。
\((1)\)规定\(a, b<1\):
\[\because a<1, b<1, \]\[\therefore ab<1, 1-ab>0, \]\[\therefore (b+\frac 1 b)-(a+\frac 1 a)<0 \]\[\therefore a+\frac 1 a>b+\frac 1 b \]\(y\)随\(x\)的增大而减小。
\((2)\)规定\(a, b>1\):
\[\because a>1, b>1, \]\[\therefore ab>1, 1-ab<0, \]\[\therefore (b+\frac 1 b)-(a+\frac 1 a)>0 \]\[\therefore a+\frac 1 a<b+\frac 1 b \]\(y\)随\(x\)的增大而增大。
其它的情况类比一下证明就可以了。
对称性
观察图像,容易发现图像关于原点对称。代数证明如下:
设函数\(y=x+\frac 1 x\)的图像上有一点\(A(t, t+\frac 1 t)\)。
\(A\)点关于原点的对称点为\(A'(-t, -t-\frac 1 t)\)。
\[\because (-t)+\frac 1 {-t}=-t-\frac 1 t \]\[\therefore A'点在函数y=x+\frac 1 x图像上。 \]由此可知,该函数图像关于原点对称。
最值(值域)
研究该函数图像的正半支。观察图像,容易发现当\(x=1\)时,函数存在最小值\(2\)。那我们如何证明呢?
\[x>0时,由基本不等式(均值定理)得: \]\[x+\frac 1 x\geq 2\sqrt {x\cdot \frac 1 x}=2 \]\[\therefore 当且仅当x=\frac 1 x即x=1时,x+\frac 1 x取得最小值2。 \]
超纲方法不能用!!!
怎么用现在已学过的知识证明?
让我们从答案往回推导一下。
要证\(x+\frac 1 x\geq 2\),即证\(x-2+\frac 1 x\geq 0\)。
诶,这个造型,像不像完全平方公式?
改一改:\((\sqrt x)^2-2\cdot \sqrt x\cdot \sqrt {\frac 1 x}+(\sqrt \frac 1 x)^2\geq 0\)
公式变形:\((\sqrt x-\sqrt \frac 1 x)^2\geq 0\),这不是理所当然的吗?
我们可以宣布可证了。
注意到:
\[(\sqrt x-\sqrt \frac 1 x)^2\geq 0 \]\[(\sqrt x)^2-2\cdot \sqrt x\cdot \sqrt {\frac 1 x}+(\sqrt \frac 1 x)^2\geq 0 \]\[x-2+\frac 1 x\geq 0 \]\[\therefore x+\frac 1 x\geq 2 \]\[当且仅当\sqrt x=\sqrt\frac 1 x即x=\frac 1 x, x=1时, \]\[x+\frac 1 x取得最小值2。 \]
现在研究\(x<0\)时的情况。根据中心对称性,可直接得:
当且仅当\(x=-1\)时,\(x+\frac 1 x\)取得最大值\(-2\)。
\(x\)、\(y\)的值域为:
\(x∈(-∞, 0)\&(0, +∞), y∈(-∞, -2)\&(2, +∞)\)。
思考
对勾函数图像是轴对称图形吗?怎么证明?
思路
由于对勾函数在\(x\)接近\(0\)时,\(y\)接近\(\frac 1 x\);在\(x\)越来越大时,\(y\)接近\(x\)。因此,两条“渐近线”为\(y\)轴和\(y=x\)。那么,我们猜测它的对称轴为\(y\)轴与\(y=x\)夹角的角平分线。学了初三就可以由三角函数得到该条直线的表达式为\(y=(\sqrt 2+1)x\)。请接着进行验证。
飘带函数
定义
定义形如\(y=kx-\frac m x(k, m为常数且k, m\neq 0)\)的函数为飘带函数。
最简单的飘带函数是\(y=x-\frac 1 x\)。让我们先研究一下它吧。
图像
掏出几何画板方格纸,并按照“列表—描点—连线”的流程画出飘带函数的图像。
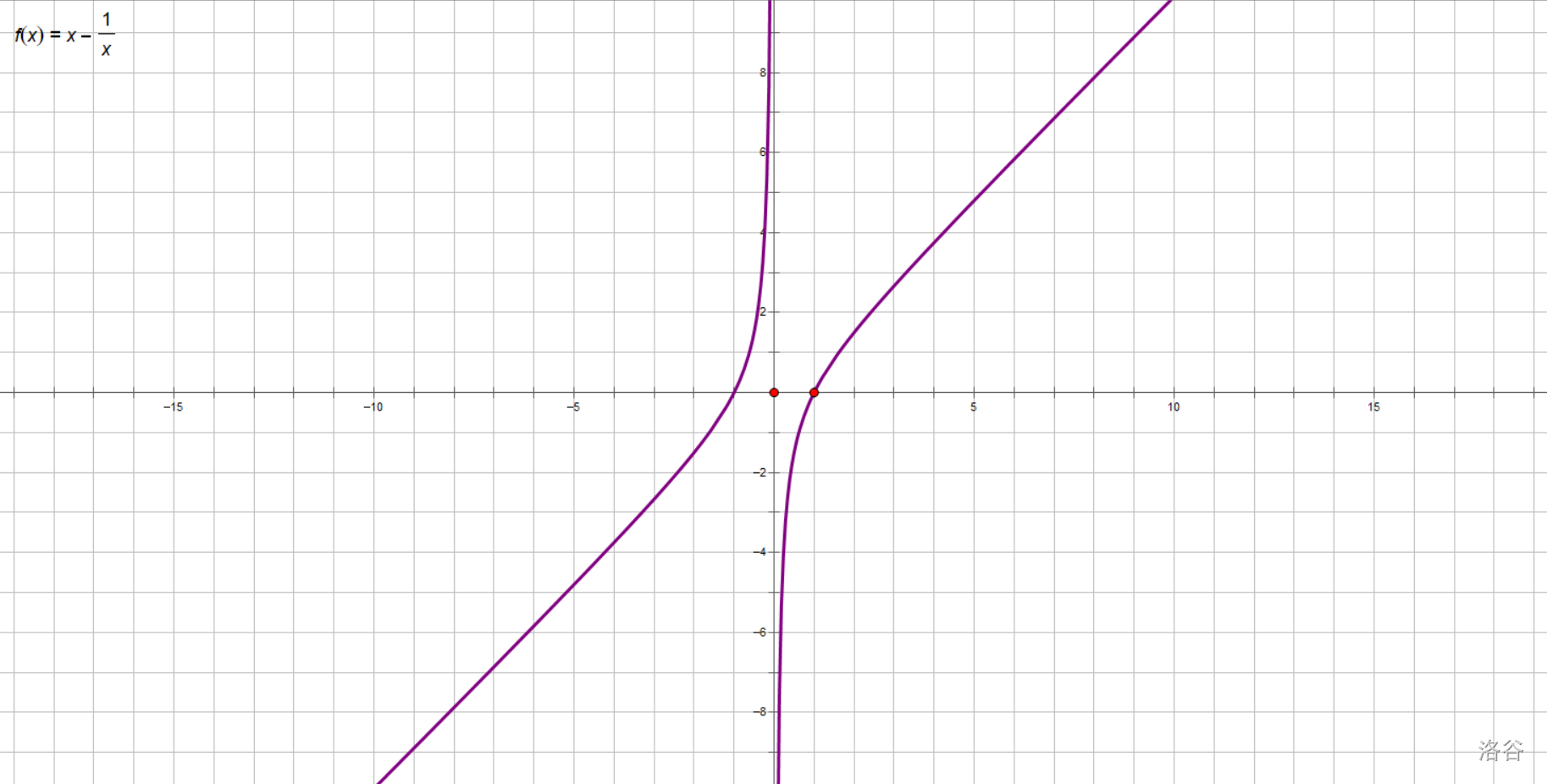
该函数的名称来源于它的图像。
性质
增减性
飘带函数的增减性比较简单。观察图像,发现它是一个双曲线,应该分两半进行探讨。
我们发现,在每一支上,都有\(y\)随\(x\)的增大而增大。
这是我们用“形”的方法看出来的。那如果用“数”的方法证明呢?
设函数\(y=x-\frac 1 x\)图像的正半支上存在两点\((a, a-\frac 1 a)\),\((b,b-\frac 1 b)\),且规定\(0<a<b\)。
作差法比大小:\[(b-\frac 1 b)-(a-\frac 1 a) \]\[=(b-a)+(\frac 1 a-\frac 1 b) \]\[=(b-a)+\frac {b-a}{ab} \]\[=\frac {(b-a)(ab+1)}{ab} \]易知\(ab>0, b-a>0\)。
\[\therefore \frac {(b-a)(ab+1)}{ab}>0 \]\[a-\frac 1 a<b-\frac 1 b \]\[y随x的增大而增大。 \]
\(x<0\)的情况类比一下证明就可以了。
对称性
观察图像,容易发现图像关于原点对称。代数证明如下:
设函数\(y=x+\frac 1 x\)的图像上有一点\(A(t, t-\frac 1 t)\)。
\(A\)点关于原点的对称点为\(A'(-t, -t+\frac 1 t)\)。
\[\because (-t)-\frac 1 {-t}=-t+\frac 1 t \]\[\therefore A'点在函数y=x-\frac 1 x图像上。 \]由此可知,该函数图像关于原点对称。
最值(值域)
\(x\)、\(y\)的值域为:
\(x∈(-∞, 0)\&(0, +∞), y∈(-∞, +∞)\)。
思考
同“对勾函数”思考。
反比例函数增长率(导数)
是时候认真思考一下这个问题了。
阅读前提示:本部分内容考试一般不考,为方老师力推拓展篇目。
一般来说,我们如何描述一个函数的增长情况?
使用诸如“\(y\)随\(x\)的增大而增大 / 减小”的术语。
那我们如何准确地描述呢?例如,如何区分下面的三条直线?
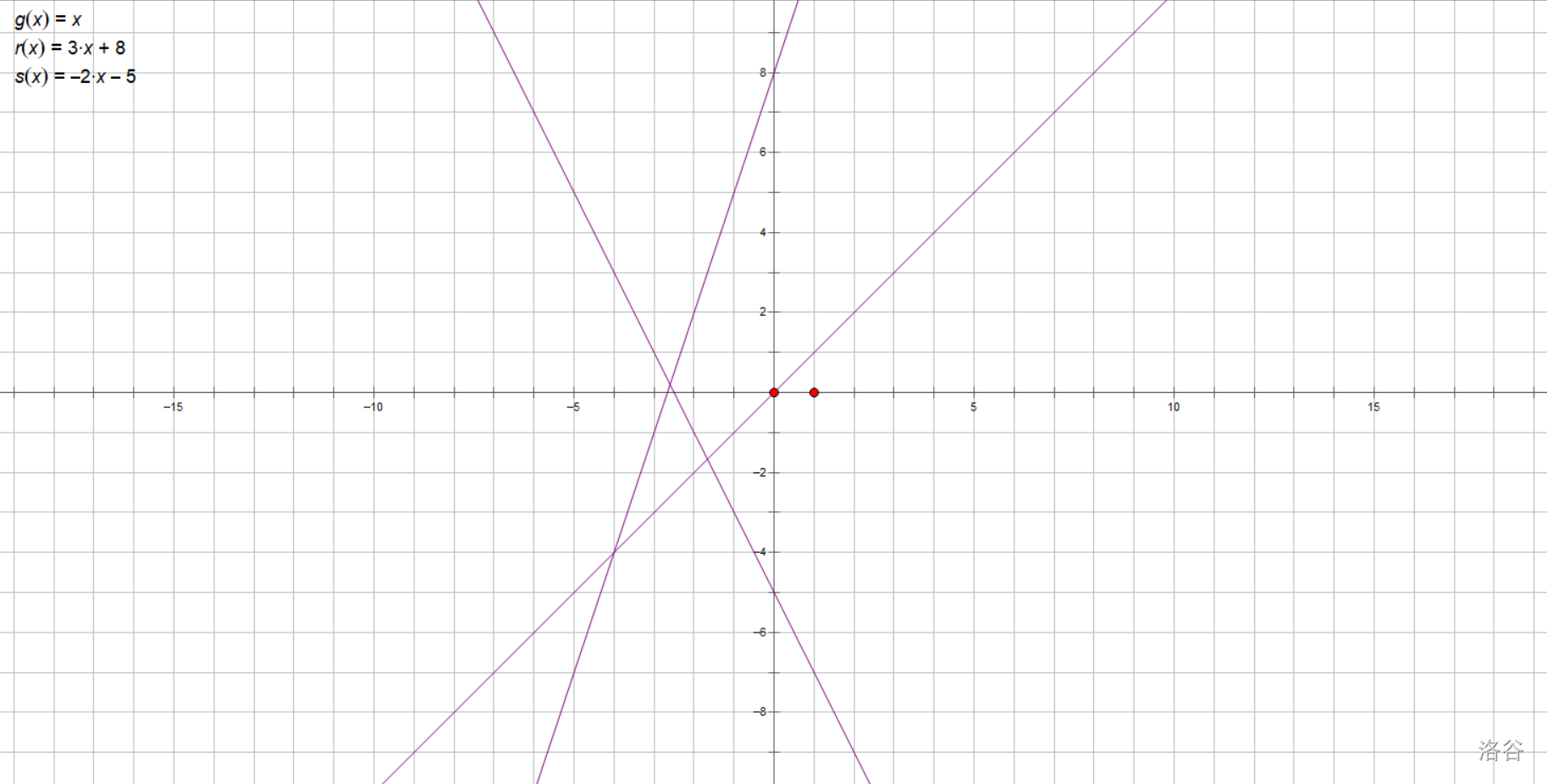
我们可以使用斜率。\(k\)的值可以反映直线的陡缓程度:
\(|k|\)越大,函数的陡缓程度越大。\(k\)的正负可反映其增减性。
一次函数的问题是解决了,那双曲线呢?
嗯……很棘手。双曲线没有办法用一个参数反映陡缓程度。那我们能否借助一次函数呢?
区间增长率
先看看第一象限的情况吧。
你应该能够发现,反比例函数的陡缓程度与\(x\)有着直接关联。因此,我们应该探讨当\(x\)取不同值时,反比例函数的陡缓程度。
然后,你凭借惊人的注意力想到,一次函数的斜率可以直接反映陡缓程度。因此,你决定在图像上的一个点处作一条切线,然后求这条切线的斜率,就像这样:
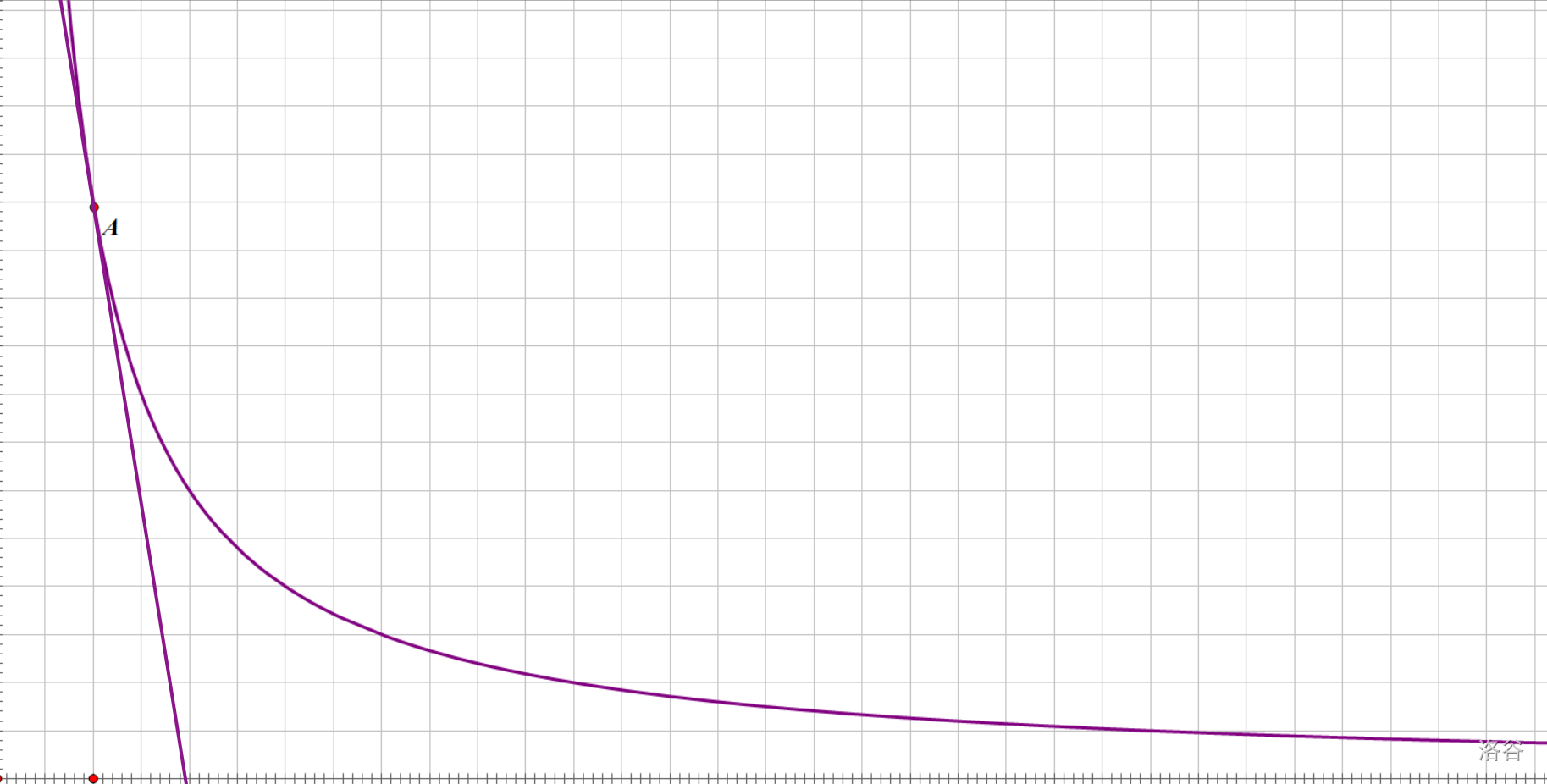
可是,醒醒吧,一个点是没法确定一条直线的。
哦!确定一条直线,至少需要两个点,那我就取两个点看看吧!
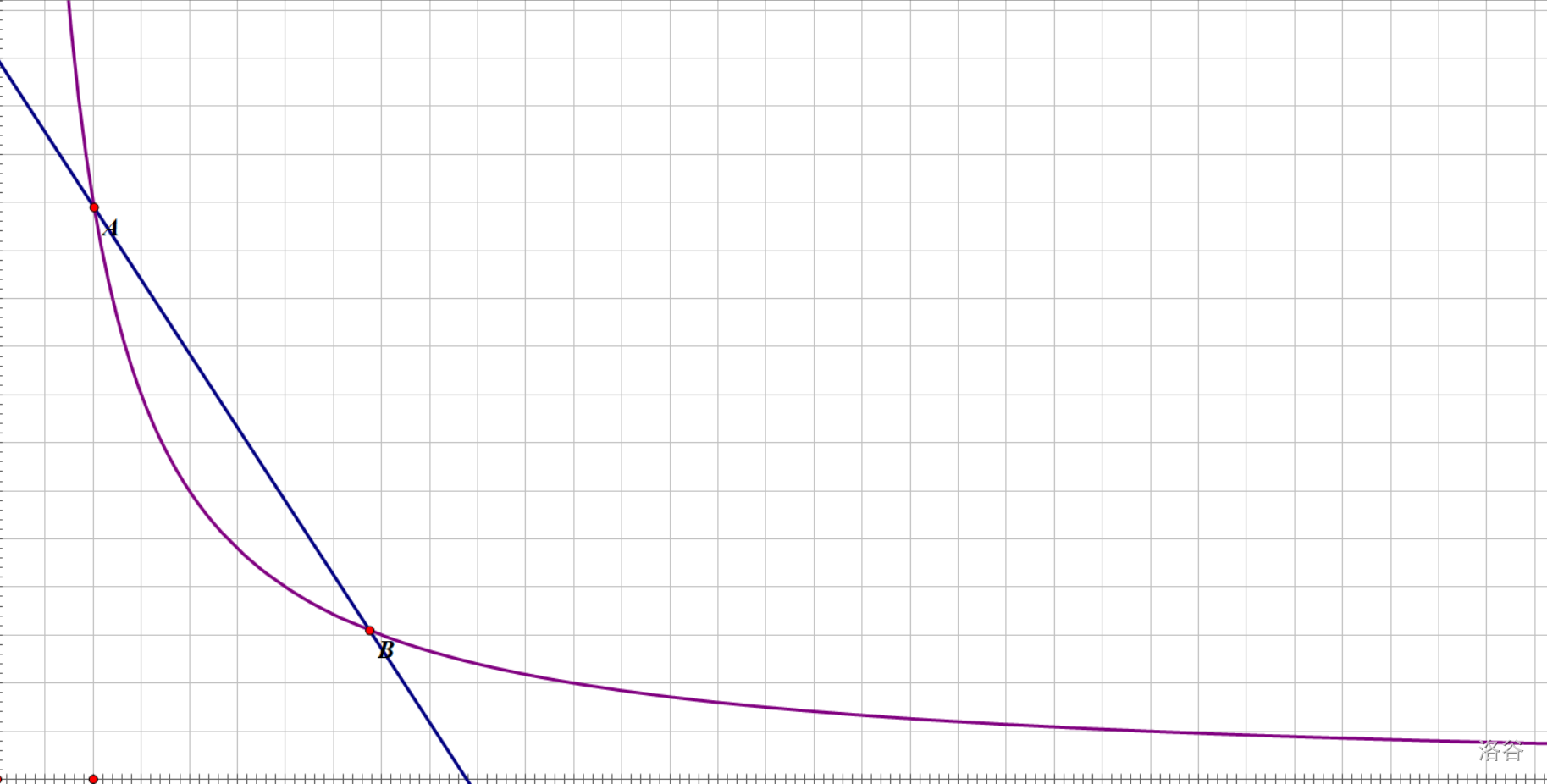
有了两个点\(A(a, \frac k a)\),\(B(b, \frac k b)\)的帮助,你很快就求出了该直线的斜率。
我们把算得的\(k\)称为反比例函数在区间\([a, b]\)的增长率。 对增长率的判别与一次函数斜率的判别完全一致。
极限\(\lim\)!
不要忘记,这还没有达到我们的要求。我们只是借助两个点部分反映了反比例函数的增长率,而离我们一个点的预期还很遥远。
但是,你发现,随着\(B\)点位置的不断变化,区间增长率\(k\)也在变化。
并且,如果你把\(A\)、\(B\)两点拉得越近,区间增长率\(k\)将越近似于\(A\)处切线的斜率。就像这样:
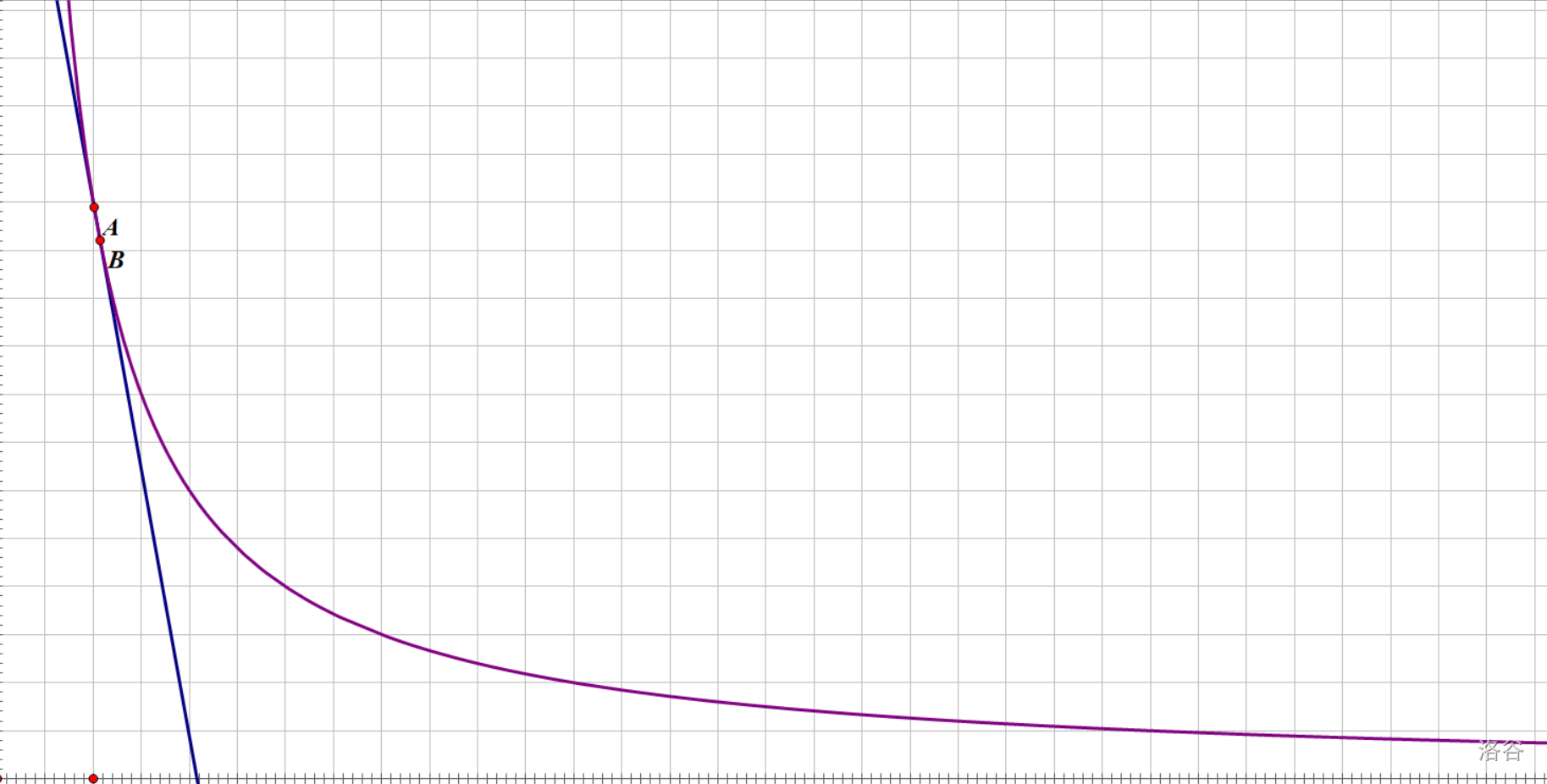
那,如果我们直接把\(A\)、\(B\)的横坐标拉成一样的呢?
需要实现这个,我们就得重新定义一下增长率了。
难道不觉得用两个未知数很麻烦吗?表示水平距离\(\Delta x\)时还需要用\(|a-b|\)。于是,我们定义:
图像上任意两点\((x, \frac k x)\)、\((x+h, \frac k {x+h})\)之间的区间增长率为\(\frac {\frac k {x+h}-\frac k x} {h}\)。
暂且规定\(h>0\)。
这样规定,是为了更好地反映“增长”这一概念。\(x\)和\(x+h\)至少比\(a\)和\(b\)更好吧。水平距离\(\Delta x\)可以直接用\(h\)表示。
接下来就是我们想要的,把\(x\)、\(x+h\)拉成一样的,即令\(h=0\)。
可是,这样的话,增长率就算不起来了,因为\(h\neq 0\)。
因此,我们想要的其实是这样的一个效果:\(h\)无限趋近于\(0\),但永远不能等于\(0\)。
什么运算可以做到这种逆天操作呢?高中生要叫起来了。
是极限。
作为初中生,当然不能硬理解,因为透彻地理解极限,是需要学完微积分才行的。那让我们对极限做一个粗糙的定义:
极限就是无限接近但永远无法到达,用符号\(\lim\)表示。
言简意赅!一针见血!
极限的格式是,在极限符号\(\lim\)下方填写未知数趋向的值,然后在右方写出表达式或等式。举一个我们之前写过的例子,就是:
这里就是说,当\(x\)无限趋向于\(0\)时,\(y\)就可以视为无穷大。这是一个不严谨的极限式。
现在,我们终于可以表示出一个点处的陡缓程度了,它就是:
稍作化简,有:
好像也就这样了。\(h\)也没有消掉啊?怎么办?
别忘了, 我们是有逆天卡片(指\(\lim\))的人。
\(h\to 0\),就是让我们把\(h\)忽略不计,那原式变为:
我们再回顾一下这个式子的意义。它代表反比例函数\(y=\frac k x\)图像在横坐标为\(x\)的点处的切线的斜率,亦即图像在横坐标为\(x\)的点处的陡缓程度。它的判别,与区间增长率保持一致,因为它们都是通过计算斜率得出的。
它有一个令人又兴奋又胆寒的名字。
导数。
到了高中,你就会知道,若计反比例函数为\(f(x)=\frac k x\),则其导函数为:
\[f'(x)=-\frac {k}{x^2} \]通俗地讲,导函数是该函数图像上所有点的横坐标及导数一一对应所组成的函数。因此,将任一横坐标代入导函数,便可直接算出该点切线的斜率。
非常的\(Amazing\)啊,反比例函数在\(x=0\)时无意义,因此它在\(x=0\)时没有导数,其导函数图像上也没有横坐标为\(0\)的点。
让我们把反比例函数\(y=\frac k x(k>0)\)的导函数的图像画出来。
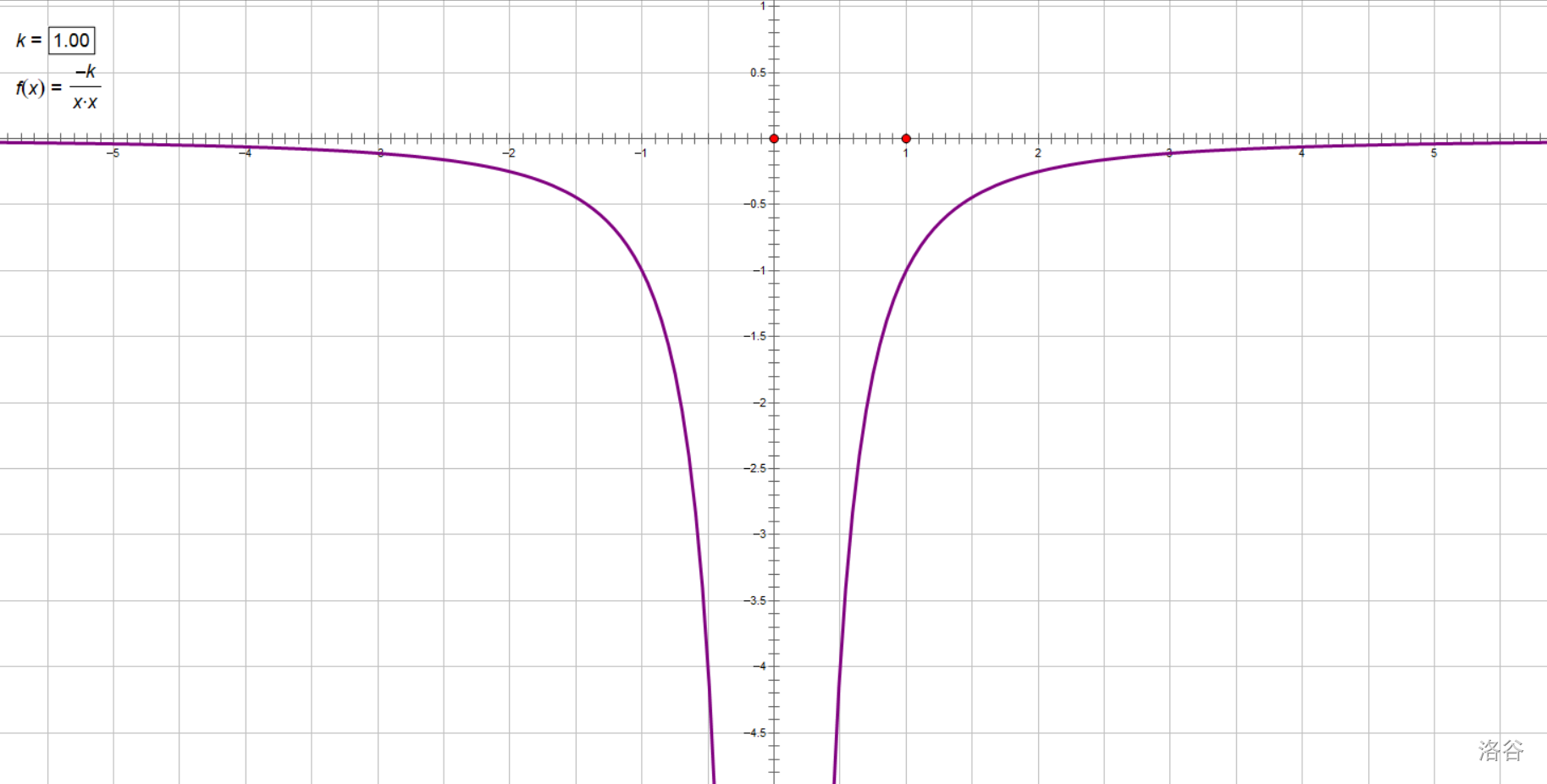
从导函数的图像上,我们可以发现一些信息:
- 图像位于\(x\)轴下方且分为\(x<0\)与\(x>0\)两段,启示我们在每一个象限内,反比例函数随\(x\)的增大而减小(导数均小于\(0\))。
- 在每一象限内,都有导函数的绝对值随\(x\)的增大而减小,启示我们在每一个象限内,反比例函数的陡缓程度随\(x\)的增大而减小。
- \(|x|\)越大,导函数越趋向于\(0\),启示我们在每一个象限内,当\(|x|\)很大时,反比例函数图像极为平缓,其切线斜率接近\(0\)。
自行探究
反比例函数增长率(导数)随参数\(k\)的变化关系。
题目汇编
只有真正有意思、有意义、有趣味的题目才会被选入。
$1. $【真正的!数形结合】
如图,在平面直角坐标系\(xOy\)中有矩形\(OABC\),其中\(A\)、\(B\)在坐标轴上,\(C\)点在第一象限内。反比例函数\(y=\frac k x\)的图像交\(AB\)、\(BC\)于点\(D\)、\(E\),恰有\(\angle AOD=\angle DOE\),且\(\angle ODE=90\degree\)。已知\(OA=3\),求\(k\)的值。
这是一道很巧妙的数形结合题。
你需要考虑一下这个角平分线该如何使用。在初二没有学过三角函数时,坐标系中角的关系必定需要转换为边的关系(特殊角除外)。那就作垂直吧,直接得到\(AD=DF\)。
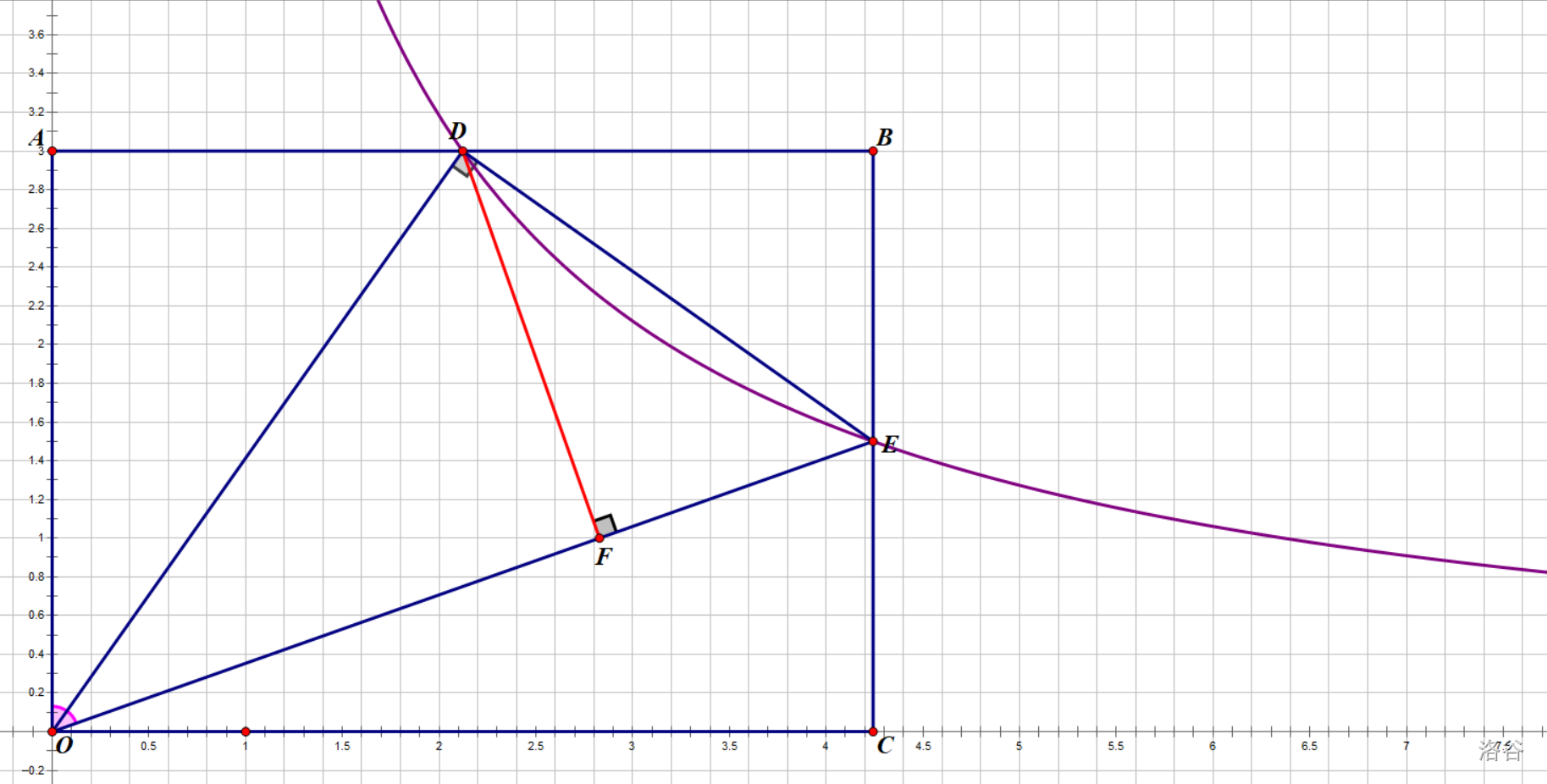
现在,就是我认为本题中最巧妙的地方了。请看\(VCR\)。
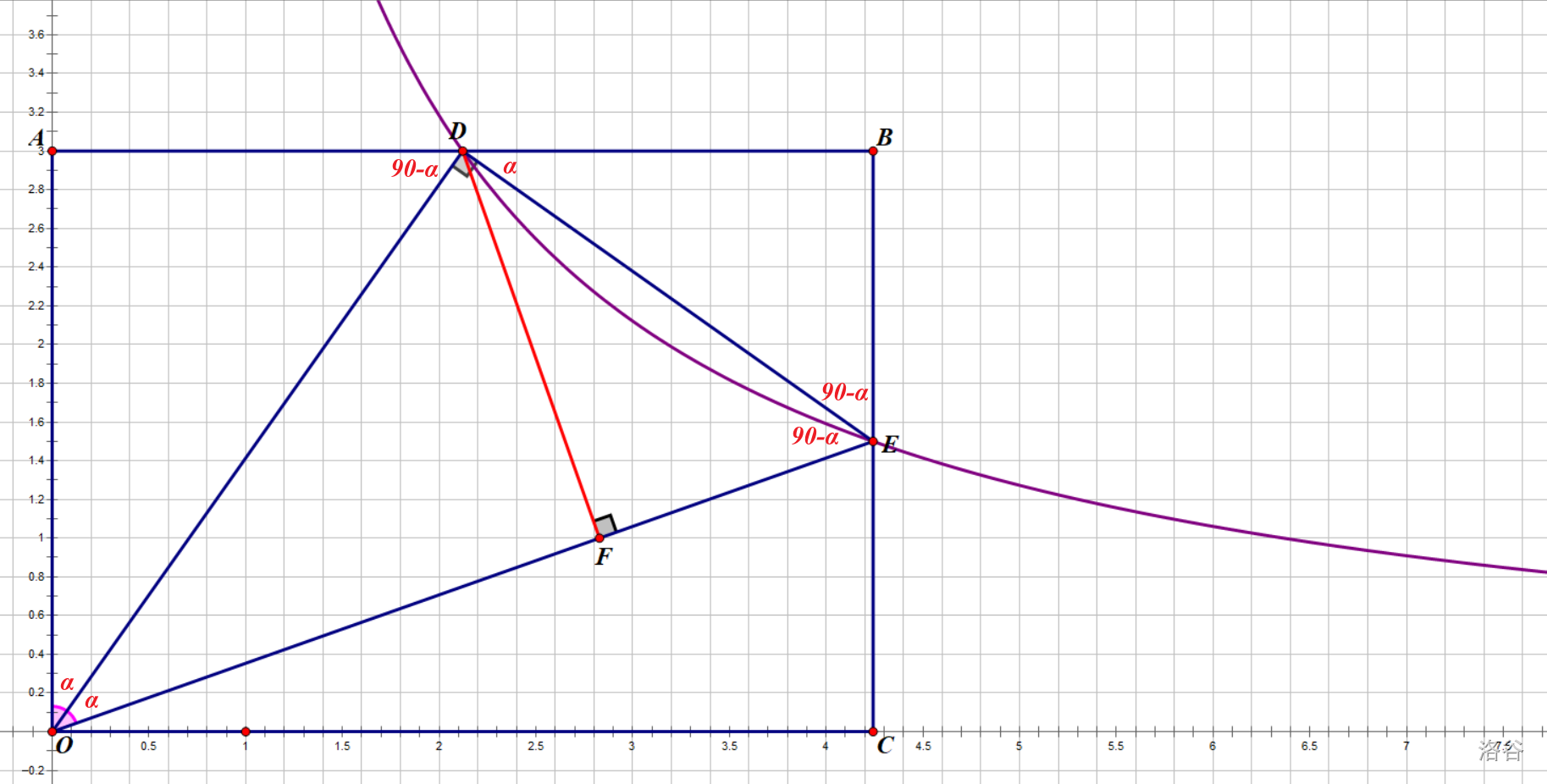
我们竟然通过设元标角,证明了\(\angle BED=\angle OED\),\(DF=BD\)!本题重要结论\(AD=BD\)就这样推出来了。
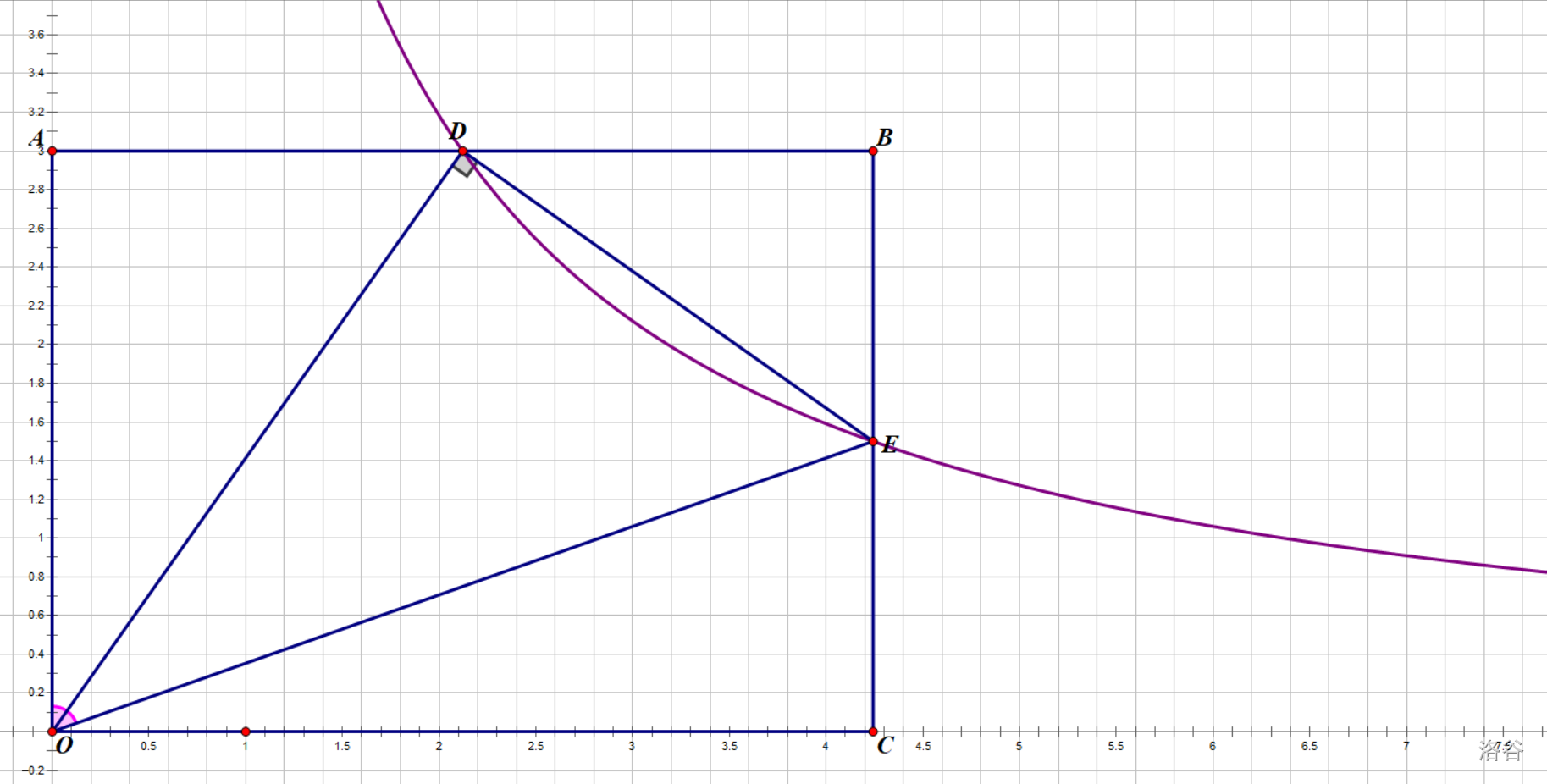
由于\(S_{\triangle AOD}=S_{\triangle OCE}=\frac k 2\),可推导\(CE=\frac {OA} 2\),实则\(E\)也是\(BC\)中点。
祖传设\(t\)大法启动。设\(D(t, 3)\),\(E(2t, 1.5)\)。因为\(D\)、\(E\)在反比例函数图像上,\(k\)一定等于\(3t\)。观察图中四个直角三角形,启示我们使用勾股定理。
解得\(k=\frac {9\sqrt 2}2\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号