可持久化线段树（随笔）

题面传送门

众所周知，可持久化线段树存了多个版本的线段树，何为多个版本？

以这道题为例，操作 1 要求我们修改某个版本的线段树；操作 2 需要访问一个版本中的值。

那么这个版本就是相对于每一次修改的不同时期的线段树。

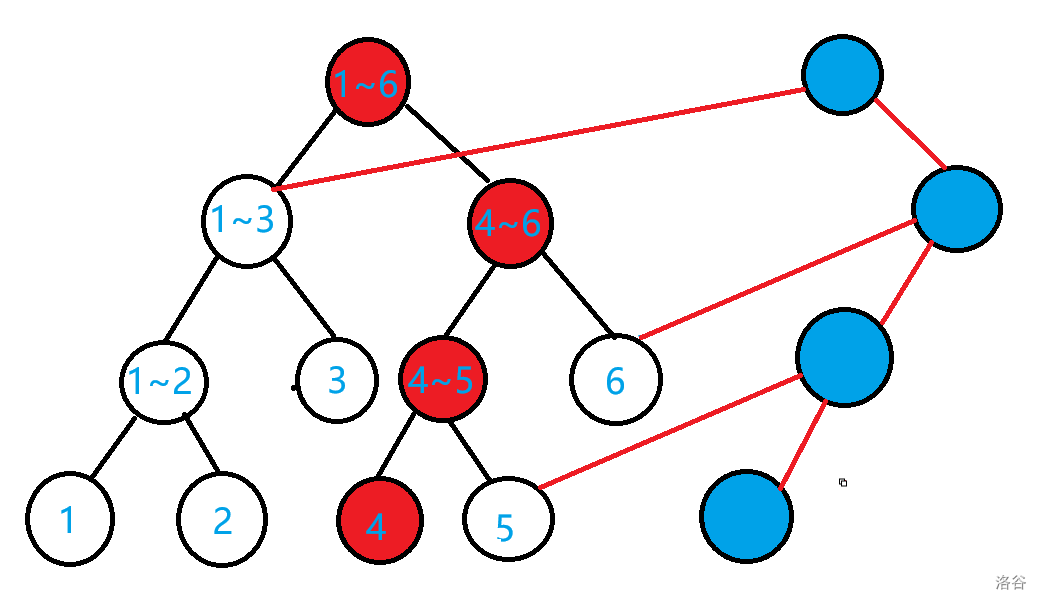
如图所示，这是一次可持久化操作，在原来这颗线段树中，我们修改了编号为 \(4\) 的这个节点。

红色的点是涉及到修改的点，是改变的点，白点是未改变的点，蓝点是新开的点。

蓝点和白点及其所连的红边和原先的边构成了新的线段树，那我们不难发现，要做到保存每一颗线段树，我们只需要根据修改的点新开一部分的点，若为单点修改，被修改的点的个数为 \(\log(n)\)，大多数的点是可以继承的，这样就节省了大量空间。

了解了思路，我们接下来就看如何具体实现：

对于这类线段树，我们需要以结构体存储（想必本来这样就要方便一点吧），
因为对于父节点 \(u\)，它的左右子节点不再不满足 \(l=2\times1,r=u\times 2+1\)，这一点同动态开点是一样的,就像这样：

struct SG{
	int l,r;
	int val;
	int ...;
}tr[N];

对于其他几个线段树的操作有：

建树：

int build(int u,int l,int r){
	u=++cnt;//赋予u节点编号
	if(l==r){
		tr[u].val=a[l];//同普通线段树的赋值
		return cnt;
	}
	int mid=l+r>>1;
	tr[u].l=build(tr[u].l,l,mid);//要给叶子节点赋值
	tr[u].r=build(tr[u].r,mid+1,r);
	return u;
}

更新:

int modify(int u,int l,int r,int x,int val){
	u=add(u);
	if(l==r){
		 
		tr[u].val=val;
	}
	else{
		int mid=l+r>>1;
		if(x<=mid){
			tr[u].l=modify(tr[u].l,l,mid,x,val);//同样的给新节点赋值
		}
		else{
			tr[u].r=modify(tr[u].r,mid+1,r,x,val);
		}
	}
	return u;
} 

与此同时还有一个额外的操作就是开新的点，对于修改操作，如果遍历到了这个 \(u\) 就说明它是涉及被修改的点。

那么我们就需要进行开点的操作，对于一个要被修改的点及其儿子，我们先从原版本复制过来，再继续遍历它的儿子，又继续开点，这样一共开 \(\log(n)\) 个点，向上传递的时候也不会影响先前的版本的值。

int add(int u){
	cnt++;
	tr[cnt]=tr[u];
	return cnt;
}

查询：

int query(int u,int l,int r,int x){
	if(l==r){
		return tr[u].val;
	}
	else{
		int mid=l+r>>1;
		if(x<=mid){
			return query(tr[u].l,l,mid,x);
		}
		else{
			return query(tr[u].r,mid+1,r,x);
		}
	}
}

还有就是我们可以看到在这份代码里，修改和建树操作都是返回了节点的值的，这是为了返回根的值以记录该版本的编号，具体见主函数内照应。

最后对于主函数：

root[0]=build(0,1,n); 
for(int i=1;i<=m;i++){
	int v,k;
	cin>>v>>k;
	if(k==1){
		int x,val;
		cin>>x>>val;
		root[i]=modify(root[v],1,n,x,val);//每当出现修改将储存一个版本
	}
	else{
		int x;
		cin>>x;
		cout<<query(root[v],1,n,x)<<endl;
		root[i]=root[v];//根据题意生成访问的版本
	}
}

完整代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
string s;
struct SG{
	int l,r;
	int val;
//	int ...
}tr[N<<5];
int cnt;
int n,m;
int a[N];
int root[N];
int build(int u,int l,int r){
	u=++cnt;
	if(l==r){
		tr[u].val=a[l];
		return cnt;
	}
	int mid=l+r>>1;
	tr[u].l=build(tr[u].l,l,mid);
	tr[u].r=build(tr[u].r,mid+1,r);
	return u;
}
int add(int u){
	cnt++;
	tr[cnt]=tr[u];
	return cnt;
}
int modify(int u,int l,int r,int x,int val){
	u=add(u);
	if(l==r){
		tr[u].val=val;
	}
	else{
		int mid=l+r>>1;
		if(x<=mid){
			tr[u].l=modify(tr[u].l,l,mid,x,val);
		}
		else{
			tr[u].r=modify(tr[u].r,mid+1,r,x,val);
		}
	}
	return u;
} 
int query(int u,int l,int r,int x){
	if(l==r){
		return tr[u].val;
	}
	else{
		int mid=l+r>>1;
		if(x<=mid){
			return query(tr[u].l,l,mid,x);
		}
		else{
			return query(tr[u].r,mid+1,r,x);
		}
	}
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);    cout.tie(0); 
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	root[0]=build(0,1,n); 
	for(int i=1;i<=m;i++){
		int v,k;
		cin>>v>>k;
		if(k==1){
			int x,val;
			cin>>x>>val;
			root[i]=modify(root[v],1,n,x,val);
		}
		else{
			int x;
			cin>>x;
			cout<<query(root[v],1,n,x)<<endl;
			root[i]=root[v];
		}
	}
	return 0;
} 

写了这道题的可以去写最经典的模板。

题目：P3834 【模板】可持久化线段树 2