笛卡尔树

笛卡尔树

这是笛卡尔树的第一个模块，重点在于介绍笛卡尔树的基本信息，以及一个笛卡尔树和二叉搜索树转化的常见 trick。

简介

笛卡尔树是一种二叉树，每个节点维护一个二元组 \((k,w)\)，要求 \(k\) 满足二叉搜索树的性质（左子树中任意权值小于根；右子树中任意权值大于根）的同时，要求 \(w\) 满足堆的性质（对于任意子树的根，根是子树中的同一种最值，最大或最小）。简单来说，对于一颗笛卡尔树，它的权值维度满足堆的性质，而它的时间戳维度满足二叉搜索树的性质。
例如：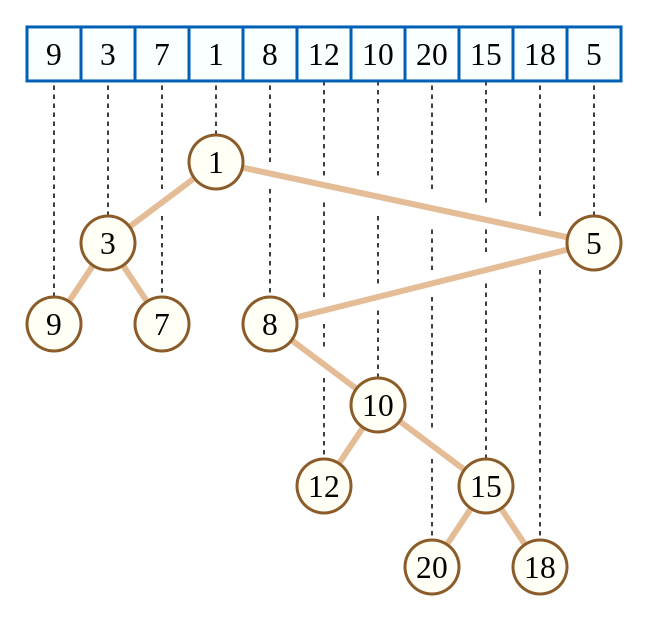
这就是一棵笛卡尔树，蓝色部分数组的值被视为 \(w\)，而数组的下标被视为 \(k\)。
通常，我们乐于让数组下标承担 \(k\) 的作用。

性质

既满足堆的性质，又满足 BST 的性质，显然，笛卡尔树是一种特殊的 Treap，也就是笛卡尔树具有 Treap 的一切性质。不同之处在于，Treap 的堆权值通常是随即处理的，然而笛卡尔树的堆权值通常有一定规律。
拓展以上性质，我们可以发现，笛卡尔树子树内的 \(k\) 权值是连续的，并且对笛卡尔树做先序遍历可以还原原本构成笛卡尔树的序列（前提是我们以下标作为 \(k\)）

构造

最常见的构造方法是利用单调栈构建笛卡尔树。
我们考虑把将要用来构建笛卡尔树的二元组按 \(k\) 的顺序排序，依次加入笛卡尔树，保证这棵树的 \(k\) 权值满足二叉搜索树性质。于是我们注意到一条最靠右的链（一直跳右儿子得到的链），它是单调递增的。
同理，从任意一个子树的根开始跑这样的右链，得到的链都是递增的。
我们考虑将元素按 \(k\) 顺序依次插入到当前的笛卡尔树中。那么每次我们插入的元素必然在这棵树的右链的末端。此时我们仍然需要维护 \(w\) 权值满足堆的性质。考虑执行这样的一个过程：自下向上比较右链节点和当前节点 \(u\) 的 \(w\)，如果出现一个右链上的节点 \(v\) 满足 \(w_v<w_u\)，就把 \(u\) 接到 \(v\) 的右儿子上，然后 \(v\)原本的右儿子都变成 \(u\) 的左儿子，那么所有性质就都满足了。
类似下面的过程：

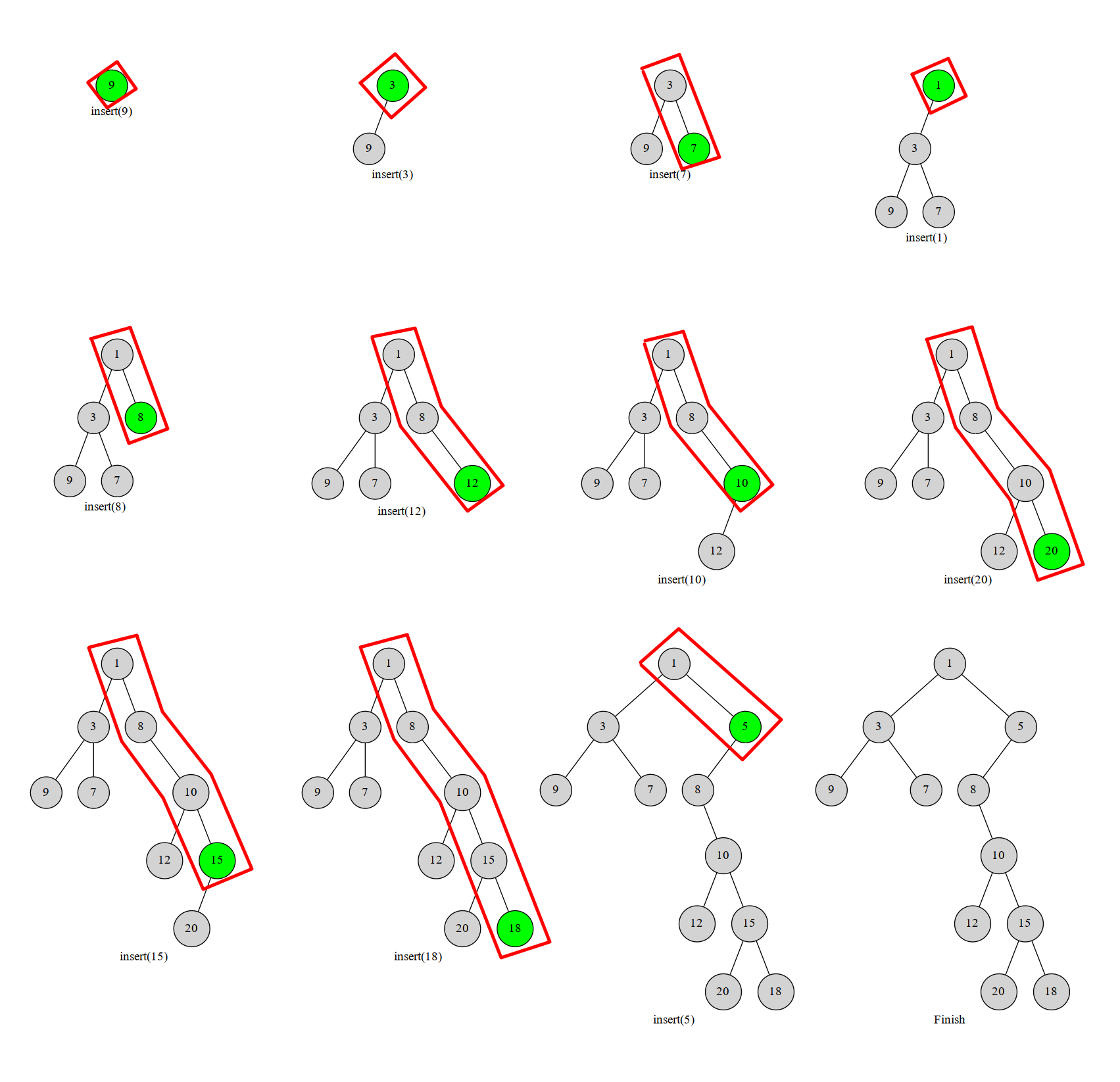
图中红框部分就是我们始终维护的右链。
显然每个数最多进出右链一次（或者说每个点在右链中存在的是一段连续的时间）。这个过程可以用栈维护，栈中维护当前笛卡尔树的右链上的节点。一个点不在右链上了就把它弹掉。这样每个点最多进出一次，复杂度 \(O(n)\)。
之前博客中提到的单调栈求最大子矩形的问题，实际上也利用了这一思想。

与二叉搜索树的关系

首先我们明确一点：如果笛卡尔树的 \(k,w\) 键值确定，且 \(k\) 互不相同，\(w\) 也互不相同，那么这棵笛卡尔树的结构是唯一的。
对于一个序列，假设我们从左到右依次把它加入一棵二叉搜索树，在二叉搜索树的每一个节点维护一个二元组 \((k,t)\) 分别对应这个点的权值和加入 BST 的时间戳，那么 \(k\) 满足了 BST 的性质，而 \(t\) 满足了小根堆的性质。
那么如果我们调换一下这两个权值，让进入树的时间——也就是序列的下标——成为权值，而让原来的权值成为时间戳，这棵树就变成了一颗笛卡尔树。
所以，对于一些情况，笛卡尔树和二叉搜索树的本质差异就在于维护二元组的先后顺序不同。
我们知道构造一棵笛卡尔树的时间复杂度是固定为 \(O(n)\) 的，然而构建一棵二叉搜索树的时间则不确定。然而对于一些各个元素均不相同的序列——例如全排列——它的笛卡尔树和二叉搜索树有且仅有一个并且对应，也就是说，除了维护的二元组相反，这两棵树的结构是完全一样的。那么对于构建全排列的二叉搜索树时间复杂度较劣的情况下，我们可以构建一棵二叉搜索树代替它。
例如P1377 [TJOI2011] 树的序：
详细证明可以参考这里的第一篇题解，下面主要关注这一题和上述 Trick 的联系。
经过分析，我们需要构造一棵二叉搜索树，得到它的先序遍历，作为答案。
然而按照提议模拟构造复杂度为 \(O(n^2)\)，不优。
此时就可以考虑转为构造一棵笛卡尔树。由于题目中的序列是全排列，所以笛卡尔树就能和二叉搜索树唯一对应，那么在笛卡尔树上 dfs 就能得到答案。
代码：

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define N 10000010

int n,a[N],b[N],flag;//a数组->时间戳 : 值；b数组->值 : 时间戳
int ls[N],rs[N],vis[N];//左儿子；右儿子；是否被访问
stack<int> stc;//单调栈，用于构建笛卡尔树

//先序遍历
void dfs(int x){
	cout<<x<<" ";
	if(ls[x]) dfs(ls[x]);
	if(rs[x]) dfs(rs[x]);
}

signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		b[a[i]]=i;
	}
	//建立笛卡尔树
	for(int i=1;i<=n;i++){
		flag=0;
		//维护单调，即维护值作为下标的单调递增
		while(stc.size()&&b[stc.top()]>b[i]){flag=stc.top();stc.pop();}
		if(stc.size()) rs[stc.top()]=i;
		if(flag) ls[i]=flag;
		stc.push(i);
	}
	for(int i=1;i<=n;i++){
		vis[ls[i]]=1;
		vis[rs[i]]=1;
	}
	for(int i=1;i<=n;i++){
		if(!vis[i]){dfs(i);break;}
	}
	return 0;
}

同类题还有P7988 [USACO21DEC] HILO G
同样利用构造笛卡尔树代替构造二叉搜索树，然后在笛卡尔树上 dfs 得到答案。
具体地，我们考虑根据样例建立的笛卡尔树：

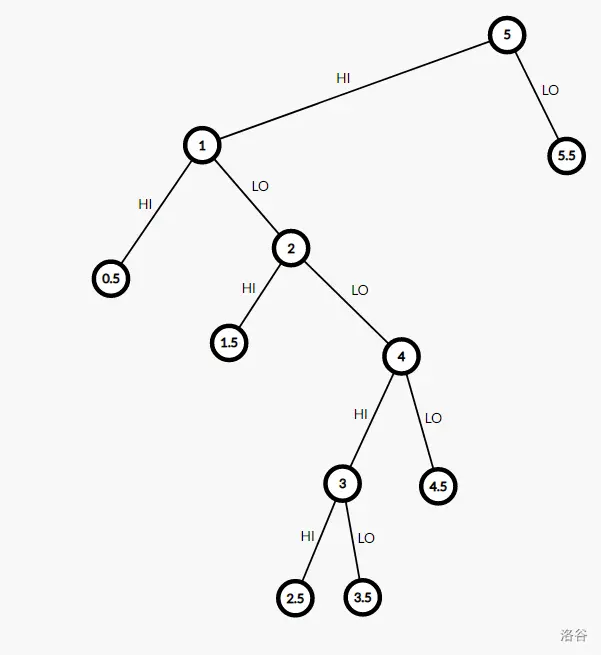
发现出现 HI 当且仅当走向左儿子。同理，得到 LO 当且仅当走向右儿子，所以在笛卡尔树上 dfs 时维护走了多少个 HILO 就行了。
代码：

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define N 200010

/*思路：考虑先把所有询问的树建出来。
由于询问得到结果后只会进入固定的一个儿子结点，所以这是一颗二叉搜索树。
由于先询问的结点会在后询问的结点上方，所以这又是一个堆。
两者一结合，正是一颗笛卡尔树。
于是我们以下标为堆的权值，原权值为二叉搜索树的权值建出一颗笛卡尔树。
遍历这颗笛卡尔树。
考虑怎样才会说出一个 HILO，显然是在树上先往左儿子走后又往右子树走，统计这种
情况的出现次数。
特别的，如果当前结点恰好是询问的那一个，会回答 LO，把这个也统计进答案即可。*/

int n,ans[N];
int a[N],b[N];

/*笛卡尔树*/
int ls[N],rs[N],vis[N],flag;
stack<int> stc;

//0为向左，代表HI；1为向右，代表LO
void dfs(int x,int fa,int cnt){//当前节点；上一步的方向；已经存在多少HILO
	if(!x) return;//没有这个节点就是走到头了
	ans[x]=cnt+(!fa);
	dfs(ls[x],0,cnt);
	dfs(rs[x],1,cnt+(!fa));
}

signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		b[a[i]]=i;
	}
	//建立笛卡尔树
	for(int i=1;i<=n;i++){
		flag=0;
		while(!stc.empty()&&b[stc.top()]>b[i]){flag=stc.top();stc.pop();}
		if(stc.size()) rs[stc.top()]=i;
		if(flag) ls[i]=flag;
		stc.push(i);
	}
	for(int i=1;i<=n;i++){
		vis[ls[i]]=1;
		vis[rs[i]]=1;
	}
	//搜索笛卡尔树得到答案
	for(int i=1;i<=n;i++){
		if(!vis[i]) dfs(i,-1,0);
	}
	for(int i=0;i<=n;i++) cout<<ans[i]<<"\n";
	return 0;
}