单调栈的运用——单调栈求最大矩形面积

单调栈求最大矩形面积

题干大约是这样：给定一个矩形网格，大小为 \(n\times m\)，每个小正方形格子大小为 \(1\times 1\)，其中有些格子能放有些不能放，问这个网格中最大的一块能放的矩形的面积。
首先想到我们肯定是要枚举每一行，来判断我们计算的矩形的底边的位置。然后我们预处理每个点最多能向上延伸多少，这个值就是在这个位置能放矩形的高度最大值。预处理以后，对于一行，我们能够得到这样的一个东西：

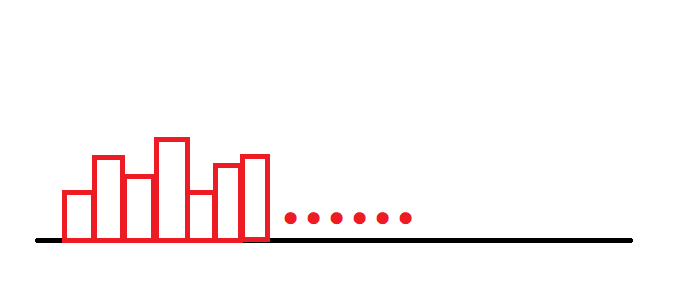
可以想到，我们枚举这些举行的所有区间，对于每个区间计算这个区间的矩形大小然后取 \(max\) 就行。
但这样子时间复杂度是 \(O(n^3)\) 的，有点劣。
我们考虑，一段小矩形组成的大矩形的面积，实际上只和这一段里最低的那个矩形的高度有关，比它高出来的部分实际上没有任何意义。
那么对于一个新加入的小矩形，它前面能更新它的位置的矩形高度一定单调不增，也就是一个上升的样子：

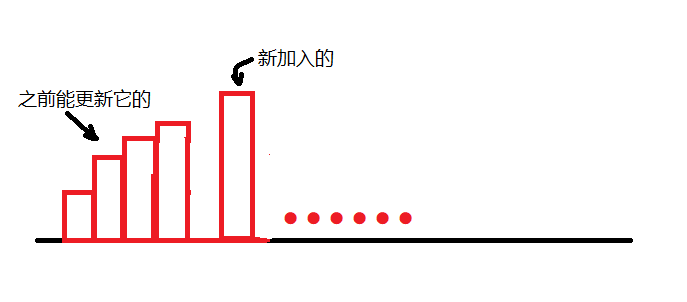
这么优美的结构，不难想到能够使用单调栈优化一下。我们钦定每个矩形在弹出时更新，这样每个举行就只需要更新一次。我们钦定每个入栈的矩形的宽度为它到它入栈前弹栈后的栈顶的距离，也就是每次弹出，更新的同时也把其宽度叠加到新入栈的矩形上：

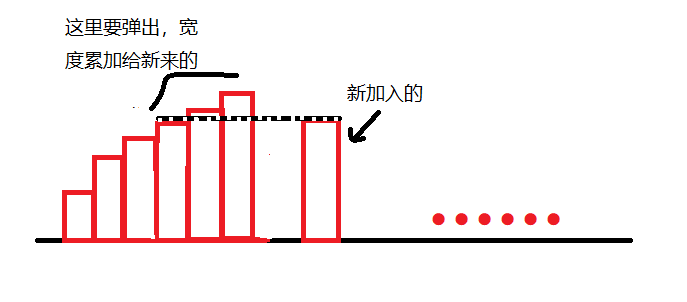
选择栈顶是因为到栈顶的这一个矩形之前还没出现过。
当我们扫完一遍所有矩形后，我们的栈里还存储着若干个矩形。此时我们需要把这些举行依次弹出，分别可最右侧的矩形取面积，这样取宽度最大：

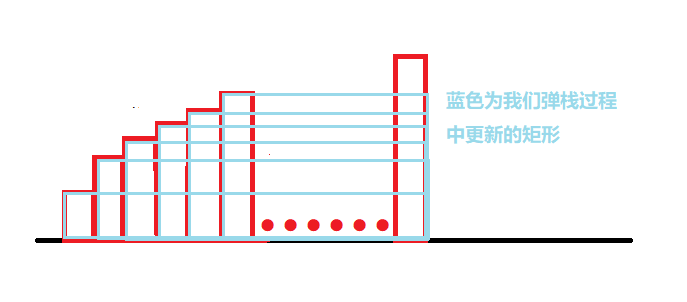
更新的所有矩形面积最大值就是最终的最大矩形面积。
这种常见的单调栈应用场景在许多题中都有应用。
例题 P4147 玉蟾宫
就是上面提到的题面的板子。见代码：

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define N 2000

/*思路需要结合图像，见博客*/

int n,m,ans,mxs;
char c;
bool mp[N][N];
int hgh[N][N];//第i行第j能向上延申的最长长度
struct node{int w,h;}S[N];
stack<node> stc;//单调栈，存储长宽

signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	memset(hgh,0,sizeof(hgh));
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>c;
			if(c=='F'){mp[i][j]=1;hgh[i][j]=hgh[i-1][j]+1;}
		}
	}
	for(int i=1;i<=n;i++){//枚举行，分别计算
		memset(S,0,sizeof(S));
		while(stc.size()) stc.pop();//清空
		//初始化：最左侧的举行宽度为1，高度为自己向上延伸最长长度
		S[1].w=1;S[1].h=hgh[i][1];
		//最左侧矩形入栈
		stc.push(S[1]);
		//枚举列，开始单调栈计算
		for(int j=2;j<=m;j++){
			int wid=0;//用于维护单调栈过程中每个新加入的矩形的宽度
			while(stc.size()&&hgh[i][j]<=stc.top().h){//维护单调
				wid+=stc.top().w;//记录弹出部分的宽度用于后续计算
				mxs=max(mxs,wid*stc.top().h);//弹出是尝试更新最大面积
				stc.pop();//弹出
			}//新加入一个矩形，则一直弹到当前栈顶弹出的矩形宽度都算上
			S[j].h=hgh[i][j];S[j].w=wid+1;//+1是因为自己宽度为1
			stc.push(S[j]);
		}
		//所有元素都入栈之后，要将栈内元素依次弹出，同时动态更新最大面积
		int wid=0;
		while(!stc.empty()){
			wid+=stc.top().w;
			mxs=max(mxs,stc.top().h*wid);
			stc.pop();
		}
	}
	ans=mxs*3;//有三个人付钱
	cout<<ans;
	return 0;
}