题解 NOIP2023 双序列拓展

题解 [NOIP2023]双序列拓展

一道有相当思维含量的注意性质题。
题目见这里。
题目要求我们把两个序列 \(f\) 和 \(g\) 进行所谓“拓展”以后进行配对，保证一个限制条件 \((f_{i}-g_{i})*(f_{j}-g_{j})\geq0\) 。
我们发现经过扩展的 \(f\) 和 \(g\) 序列长度能够达到 \(10^{100}\) ,这是一个近乎无线的量级，所以我们无法得到 \(f\) 和 \(g\) 拓展后的完整序列。
我们考虑这个拓展并匹配的过程。我们发现，所谓扩展之后匹配实际上相当于一个序列的某个点同时和另一个的序列的多个点匹配。以此类推，\(f\) 和 \(g\) 的匹配类似于下面这种样子：

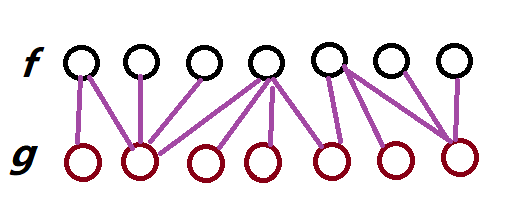
由这种排列形式，我们不难得出一下规律：

1. 允许一配多。
2. 配对不交叉。也就是说，每一次配对时，一定是两个序列中还没配对的编号最小的两个点进行配对。
3. 只要我们能最终让 \(f_{n}\) 和 \(g_{m}\) 进行配对，则扩展后的序列一定存在合法配对。
4. 序列中所有配对的限定条件和 \(f_{1}\rightarrow g_{1}\) 的配对条件一致。也就是，如果我们钦定 \(f_{1}<g_{1}\) 则以后所有配对都必须满足 \(f_{i}<g_{i}\) ，反之同理。

于是想到暴力dp，设 \(dp_{i,j}\) 表示 \(f\) 匹配到第 \(i\) 位，\(g\) 匹配到第 \(j\) 位能否成功配对。假定当前配对规则为 \(f_{i}<g_{i}\) ，则容易得到转移：\(dp_{i,j}=dp_{i-1,j} \lor dp_{i,j-1} \lor dp_{i-1,j-1}\)，也就是说三种可能的前一组匹配的方式只要有一个能够成功那么就能向后移到当前位置。最后检查 \(dp_{n,m}\) 是否合法即可。而对于 \(f_{i}>g_{i}\) 的条件也同理，修改初始第一组的判定条件即可。如果两种条件存在一种合法，那么当前的两个序列就合法。
但我们发现，这种dp起手状态就是 \(n^2\) 种，其复杂度必然不低于 \(O(n^2)\)，复杂度过高。
我们继续展开思考。我们发现，题目给出了一条特殊性质：对于每组询问（包括初始询问和额外询问），保证 \(x_1 < y_1\)，且 \(x_n\) 是序列 \(X\) 唯一的一个最小值，\(y_m\) 是序列 \(Y\) 唯一的一个最大值。
所以我们转而关注两个序列的最值。我们尝试把两个序列的匹配放到二维平面上，令横向代表 \(f\) ，竖向代表 \(g\) ，如果能够匹配则交点处填 1 ,不能匹配则填 0。则我们的目标就变成了检查在这个平面上是否存在一条全为 1 的路径能够从点 \((1,1)\) 走到点 \((n,m)\)，像这样：

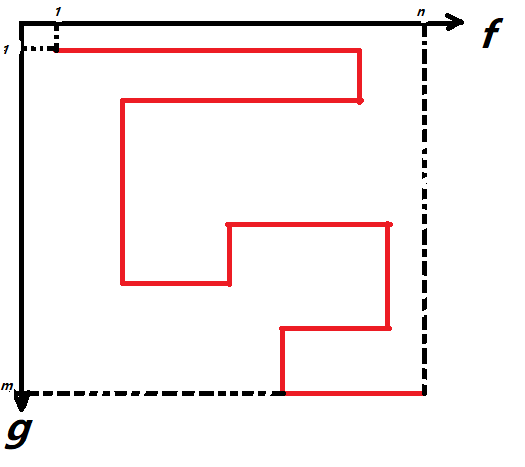
这时考虑特殊性质。由于 \(f_{m}\) 是 \(f\) 的唯一最小值，\(g_{m}\) 是 \(g\) 的唯一最大值，并且钦定了匹配条件为 \(f_i < g_i\)，所以 \(f_{n}\) 必然能和任意的 \(g_i\) 匹配。同理 \(g_{m}\) 必然能和任意的 \(f_i\) 匹配，也就是平面上的第 \(n\) 列和第 \(m\) 行都是 1，像这样：

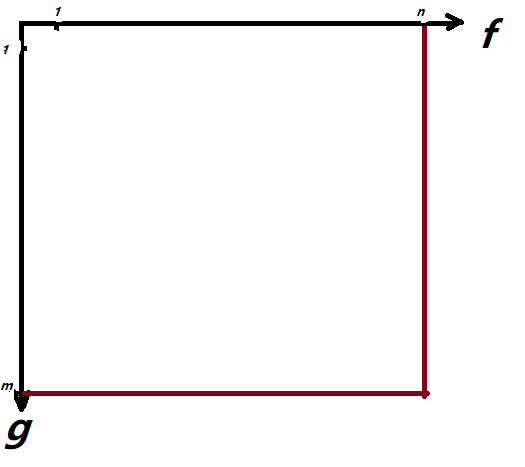
于是我们只需要判断从 \((1,1)\) 能否走到 \((n-1,m-1)\) 即可，也就缩小了范围。
那么我们重复这个找到最小值然后跳过去的过程，就能不断缩小范围，直到我们缩到 \((1,1)\)。如果能一直操作下去，就说明当前方案合法，像这样：

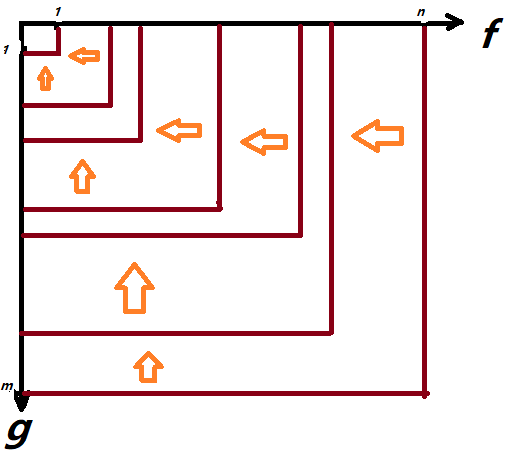
那么什么时候不能继续匹配呢？我们思考，如果存在 \(f_{min}\ge g_{min}\)，则 \(f_{min}\) 所在的那一列不能和任意的 \(g_i\) 匹配，也就是全为 0，于是所有路径均被切断，一定不合法；同理，如果出现 \(f_{max}\ge g_{max}\)，则会出现一行 0，也一定不合法。
所以我们预处理出 \(f\)，\(g\) 序列的前缀 \(max\) 和前缀 \(min\) 的值和位置，然后递归地向 \((1,1)\) 不停地跳 \(pos_{f_{min}}\) 和 \(pos_{g_{max}}\)，直到不合法退出或者走到终点。另一种判定条件也同理，交换过来就行。然后两种方式只要有一种成功就能成功。
那么对于一般的情况呢？我们还是延续之前的思路，钦定 \(f_i<g_i\)，则先找到 \(f_{min}\) 和 \(g_{max}\) 的位置，则大约像这样：

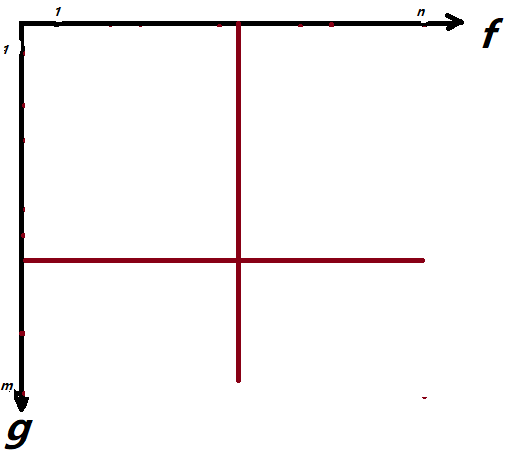
显然，比起特殊性质，仅仅是初始的位置已到了中间。那么为了能够合法，我们必须保证从红线位置不仅能走到左上 \((1,1)\) 的位置，还能走到右下 \((n,m)\) 的位置。
不妨处理出两个序列的前后缀最值和它们的位置，然后对于左上、右下两个方向，分别递归判定一次即可。
另一种情况也一样，最后两种方式只要有一种成功就能成功。
于是这题就做完了，看代码：

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define N 500010

/*解析需要配合图片，详见博客*/

string ans;
int c,n,m,q,x,y,p,v;
int X[N],Y[N],a[N],b[N];
int tmpx[N],tmpy[N];//记录原始版本
bool f1,f2;//两头判断

int amin[N],amax[N];//a序列前缀min和前缀max
int bmin[N],bmax[N];//b序列前缀min和前缀max
int mnpa[N],mnpb[N];//两个序列前缀min的位置
int mxpa[N],mxpb[N];//两个序列前缀max的位置

int ramin[N],ramax[N];//a序列后缀min和后缀max
int rbmin[N],rbmax[N];//b序列后缀min和后缀max
int rmnpa[N],rmnpb[N];//两个序列后缀min的位置
int rmxpa[N],rmxpb[N];//两个序列后缀max的位置

void init1(int n,int m){//预处理前缀min/max和其位置
	amin[0]=bmin[0]=2e9; amax[0]=bmax[0]=0;
	mnpa[0]=mnpb[0]=mxpa[0]=mxpb[0]=0;
	for(int i=1;i<=n;i++){
		if(a[i]>amax[i-1]){amax[i]=a[i];mxpa[i]=i;}
		else{amax[i]=amax[i-1];mxpa[i]=mxpa[i-1];}
		if(a[i]<amin[i-1]){amin[i]=a[i];mnpa[i]=i;}
		else{amin[i]=amin[i-1];mnpa[i]=mnpa[i-1];}
	}
	for(int i=1;i<=m;i++){
		if(b[i]>bmax[i-1]){bmax[i]=b[i];mxpb[i]=i;}
		else{bmax[i]=bmax[i-1];mxpb[i]=mxpb[i-1];}
		if(b[i]<bmin[i-1]){bmin[i]=b[i];mnpb[i]=i;}
		else{bmin[i]=bmin[i-1];mnpb[i]=mnpb[i-1];}
	}
	return;
}

void init2(int n,int m){//预处理后缀min/max和其位置
	ramin[n+1]=rbmin[m+1]=2e9; ramax[n+1]=rbmax[m+1]=0;
	rmnpa[n+1]=rmnpb[m+1]=rmxpa[n+1]=rmxpb[m+1]=0;
	for(int i=n;i>=1;i--){
		if(a[i]>ramax[i+1]){ramax[i]=a[i];rmxpa[i]=i;}
		else{ramax[i]=ramax[i+1];rmxpa[i]=rmxpa[i+1];}
		if(a[i]<ramin[i+1]){ramin[i]=a[i];rmnpa[i]=i;}
		else{ramin[i]=ramin[i+1];rmnpa[i]=rmnpa[i+1];}
	}
	for(int i=m;i>=1;i--){
		if(b[i]>rbmax[i+1]){rbmax[i]=b[i];rmxpb[i]=i;}
		else{rbmax[i]=rbmax[i+1];rmxpb[i]=rmxpb[i+1];}
		if(b[i]<rbmin[i+1]){rbmin[i]=b[i];rmnpb[i]=i;}
		else{rbmin[i]=rbmin[i+1];rmnpb[i]=rmnpb[i+1];}
	}
	return;
}

bool check1(int x,int y,int n,int m){//左上部分的检查
	if(x==1||y==1) return 1;
	if(amin[mnpa[x-1]]<bmin[mnpb[y-1]]) return check1(mnpa[x-1],y,n,m);
	if(bmax[mxpb[y-1]]>amax[mxpa[x-1]]) return check1(x,mxpb[y-1],n,m);
	return 0;
}

bool check2(int x,int y,int n,int m){//右下部分的检查
	if(x==n||y==m) return 1;
	if(ramin[rmnpa[x+1]]<rbmin[rmnpb[y+1]]) return check2(rmnpa[x+1],y,n,m);
	if(rbmax[rmxpb[y+1]]>ramax[rmxpa[x+1]]) return check2(x,rmxpb[y+1],n,m);
	return 0;
}

bool solve(bool op,int n,int m){
	if(op==1){for(int i=1;i<=n;i++) a[i]=X[i];
			for(int i=1;i<=m;i++) b[i]=Y[i];}
	else{for(int i=1;i<=n;i++) a[i]=Y[i];
		for(int i=1;i<=m;i++) b[i]=X[i];}
	init1(n,m); init2(n,m);
	//找到两条分割线的位置，开始检查
	//特判优化
	if(amin[mnpa[n]]>=bmin[mnpb[m]]||amax[mxpa[n]]>=bmax[mxpb[m]]) return 0;
	return check1(mnpa[n],mxpb[m],n,m)&&check2(mnpa[n],mxpb[m],n,m);
}

signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>c>>n>>m>>q;
	for(int i=1;i<=n;i++){cin>>X[i];tmpx[i]=X[i];}
	for(int i=1;i<=m;i++){cin>>Y[i];tmpy[i]=Y[i];}
	//第一轮判断
	//正反两方向满足其一即可满足
	if(solve(0,m,n)||solve(1,n,m)) ans+='1';
	else ans+='0';
	//额外询问
	while(q--){
		cin>>x>>y;
		for(int i=1;i<=n;i++) X[i]=tmpx[i];
		for(int i=1;i<=m;i++) Y[i]=tmpy[i];
		for(int i=1;i<=x;i++){cin>>p>>v;X[p]=v;}
		for(int i=1;i<=y;i++){cin>>p>>v;Y[p]=v;}
		if(solve(0,m,n)||solve(1,n,m)) ans+='1';
		else ans+='0';
	}
	cout<<ans;
	return 0;
}