AC自动机

AC自动机

自动机，一般指代“有限状态自动机”，可以理解为一套类似于图的系统，每个节点标识一个状态，状态之间存在相互关系。当状态接收到不同指令时，将向不同状态进行转移
AC自动机是一种基于字典树和KMP匹配思想的自动机，在处理字典树上的问题时具有卓越表现。AC自动机主要用于进行字典树上的匹配任务，也就是对于给定的一些模式串，查询他们在目标串中是否出现、出现次数等信息

实现

初始时，AC自动机将获取一些模式串，此处记为\(s_{1},s_{2},...,s_{n}\)。建立一颗字典树，按照普通字典树建树的方法吧这些串插入字典树中
显然，此时字典树中的某个节点一定是某个字符串的前缀，把节点称为状态，字典树的边就是状态的转移。那么，如何做到模式串的匹配呢？

失配指针

AC自动机利用一个叫做失配指针（fail指针）的系统辅助进行多个模式串的匹配
当我们的某个模式串在匹配目标串\(t\)的某个字母时匹配失败（字母不同），称这样的状态为失配状态。这时，为了能够在最大限度利用已经处理过的信息的基础上顺利开始匹配下一部分的模式串，需要跳到一个特殊的位置——当前状态u的最长后缀v所在的位置

如何构造fail指针

构造失配指针时，可以参考KMP的指针构建方式。考虑字典树中当前的结点u，u的父结点是p，p通过字符c的边指向u，即\(\operatorname{trie}(p, c)=u\)。假设深度小于u的所有结点的fail指针都已求得。
1.如果\(\operatorname{trie}(\operatorname{fail}(p), c)\)存在：则让u的fail指针指向\(\operatorname{trie}(\operatorname{fail}(p), c)\)。相当于在p和\(\operatorname{fail}(p)\)后面加一个字符c，分别对应u和 \(\operatorname{fail}(u)\)
2.如果\(\operatorname{trie}(\operatorname{fail}(p), c)\)不存在：那么我们继续找到\(\operatorname{trie}(\operatorname{fail}(\operatorname{fail}(p)), c)\)。重复判断过程，一直跳fail指针直到根结点
3.如果依然不存在，就让fail指针指向根结点
在实际操作时，可以通过bfs遍历所有节点，按照bfs序求解失配指针，可以保证上层比下层先求出，如图：

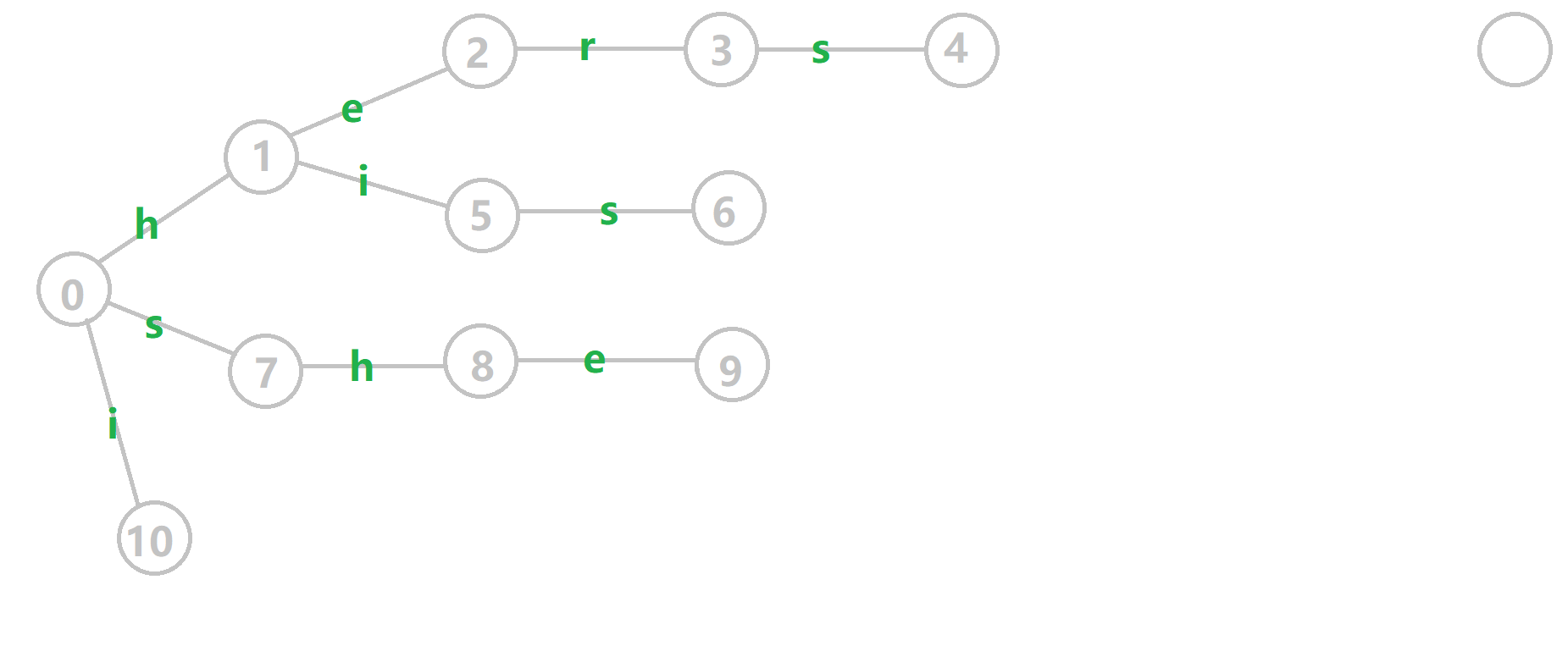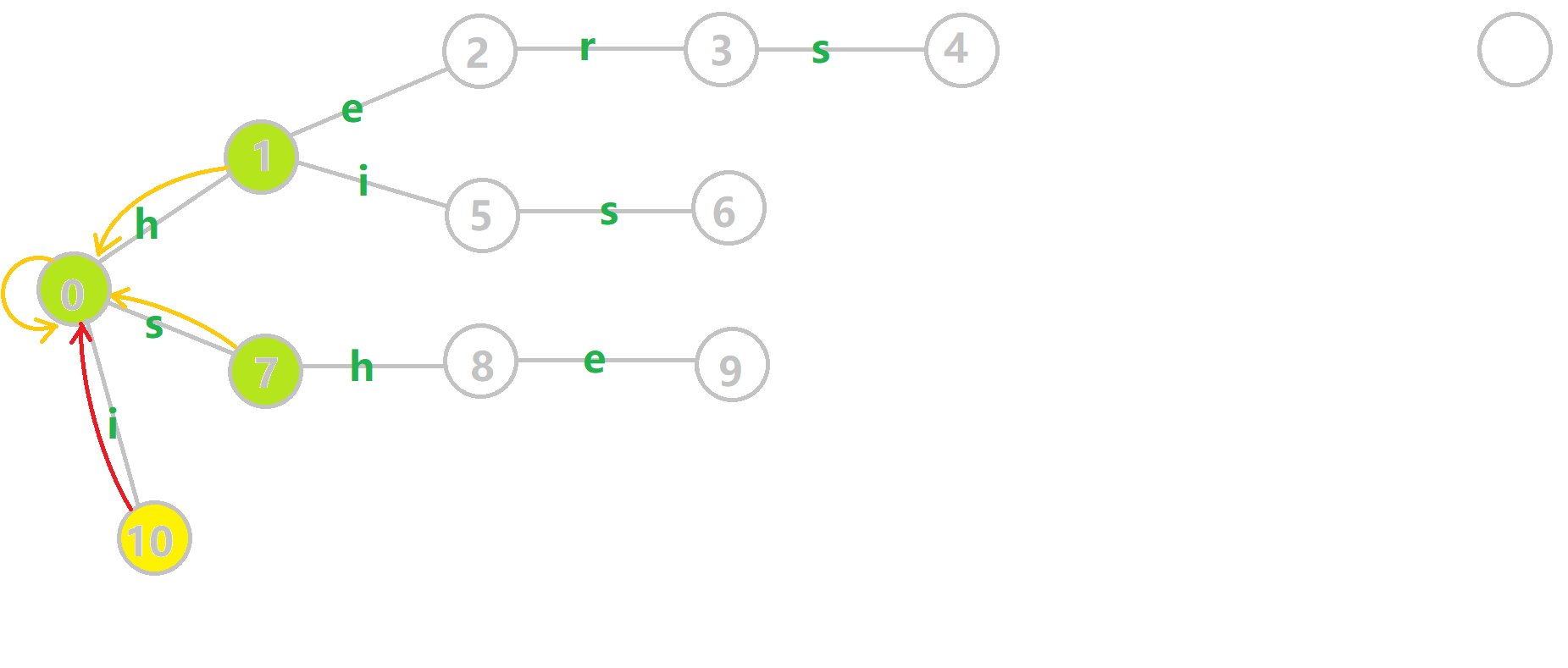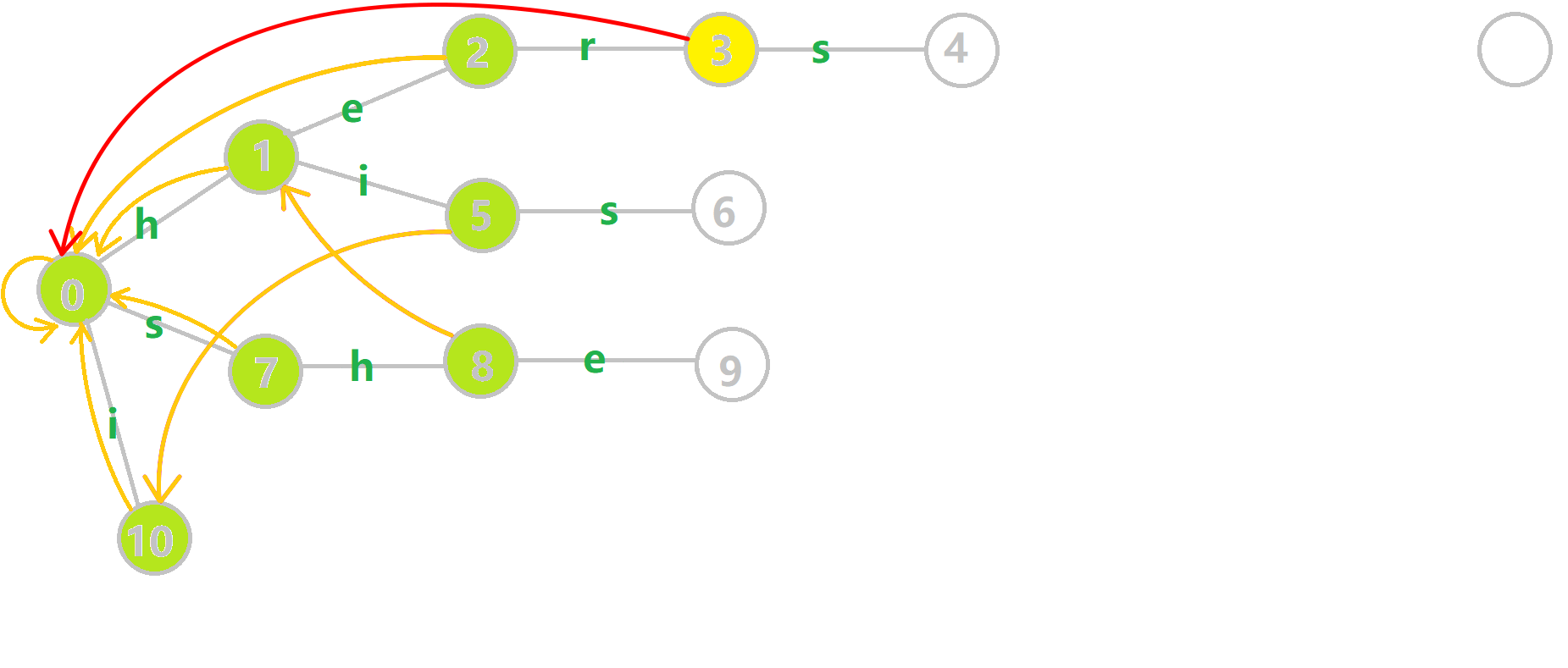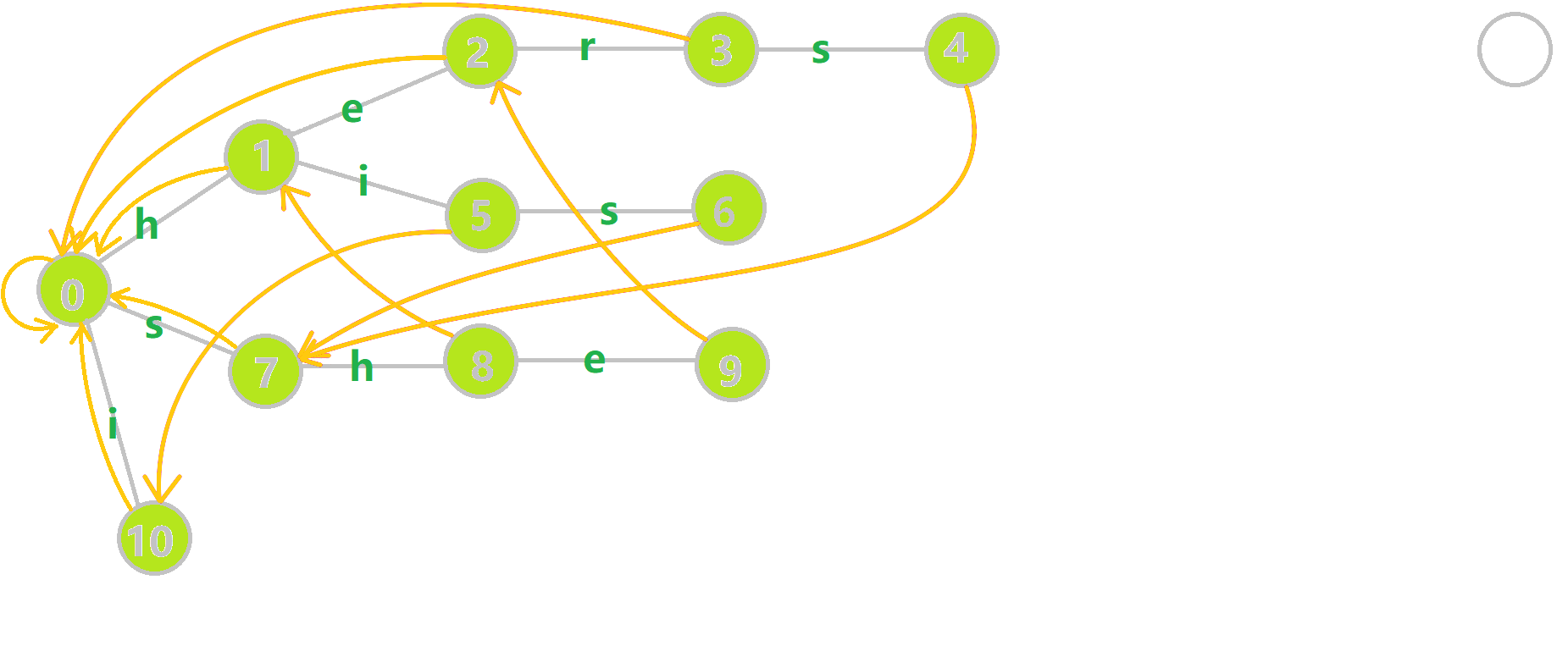
黄色结点：当前的结点 u。
绿色结点：表示已经 BFS 遍历完毕的结点。
橙色的边：fail 指针。
红色的边：当前求出的 fail 指针

构造

如上文所说，对字典树进行一次bfs，途中一边更新自动机一边更新fail数组(存储所有fail指针)。对于某一条连边，视为某个状态的串通过加减一个字符可疑转移到下一个状态，记为\(trans(u,c)\)
bfs时，由于根节点是固定的，初始时直接把根的儿子们全部入队。每次弹出一个节点，遍历它的字符集（a~z），判断能否转移。如果能够转移也就是\(trans(u,c)\)存在，就按照fail指针的构建规则把\(trans(u,c)\)的fail赋值为\(trans(fail(u),c)\)。否则令\(trans(u,c)\)指向\(trans(fail(u),c)\)的状态也就是其儿子，保证字典图的完整结构
此时可以发现，理论上我们应当对于每个可能情况不停地在fail数组上寻找可以转移的点，所以可以用son数组直接记录下一个可以转移的位置来保证时间复杂度
如图：

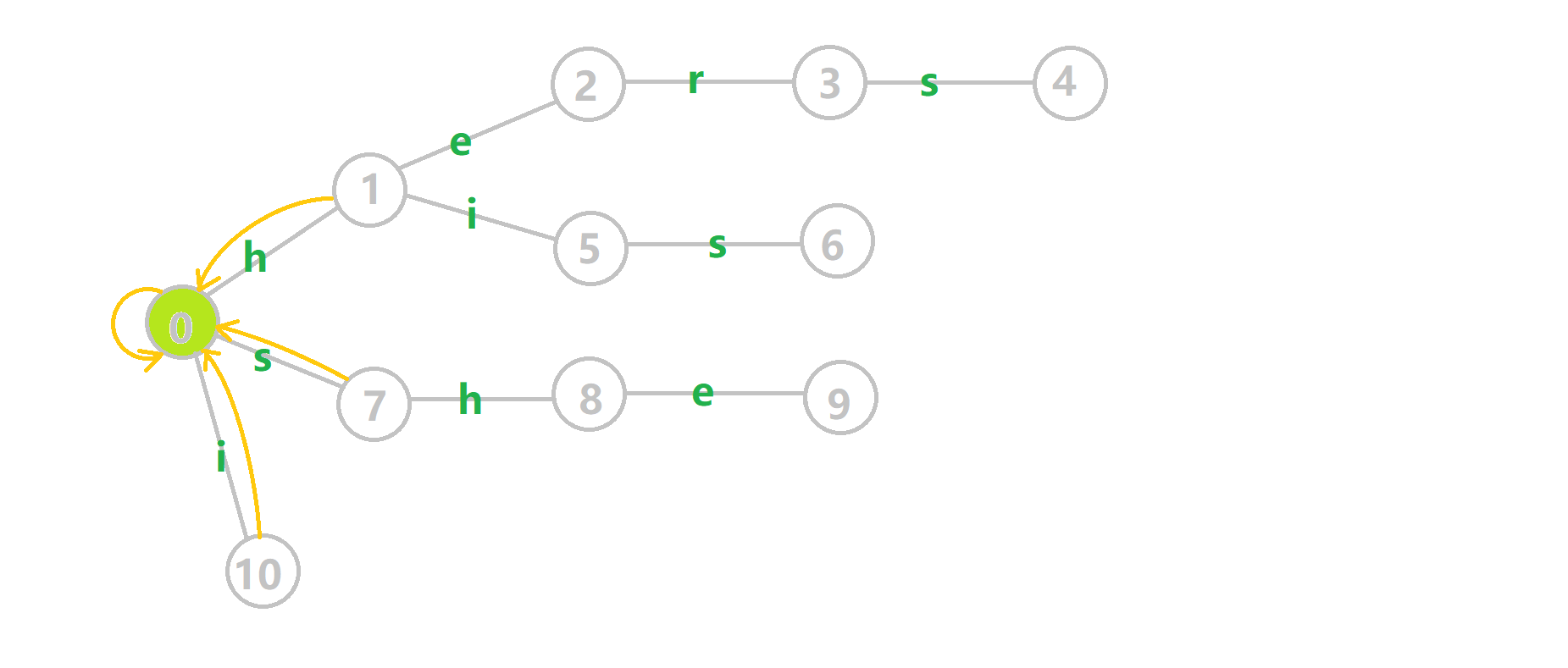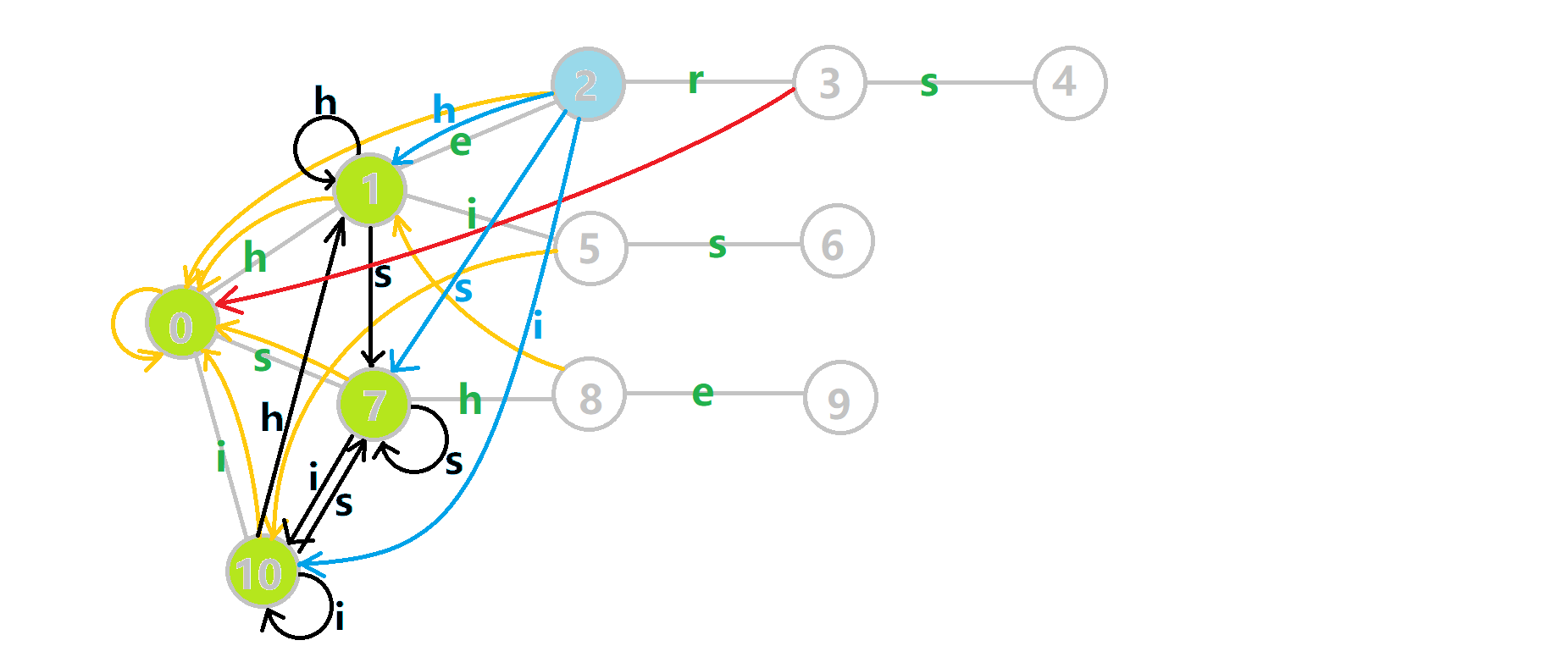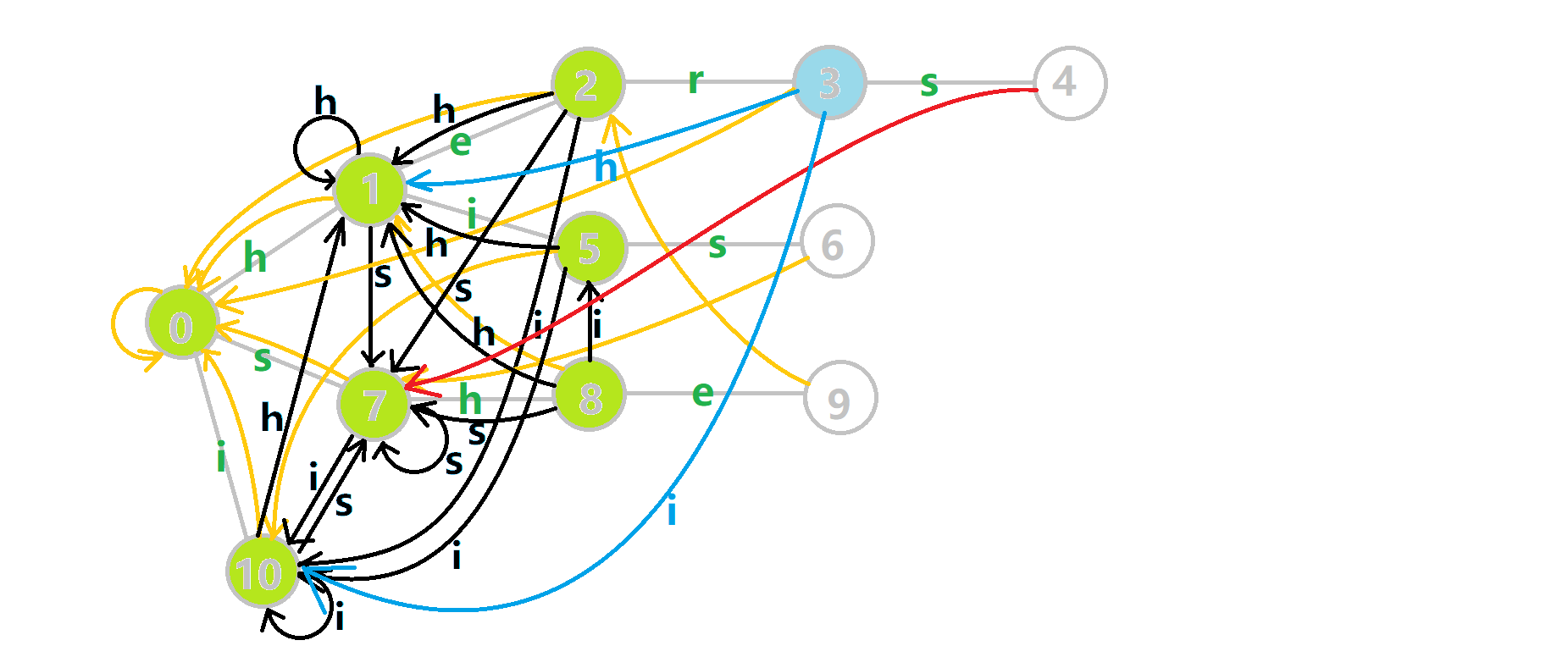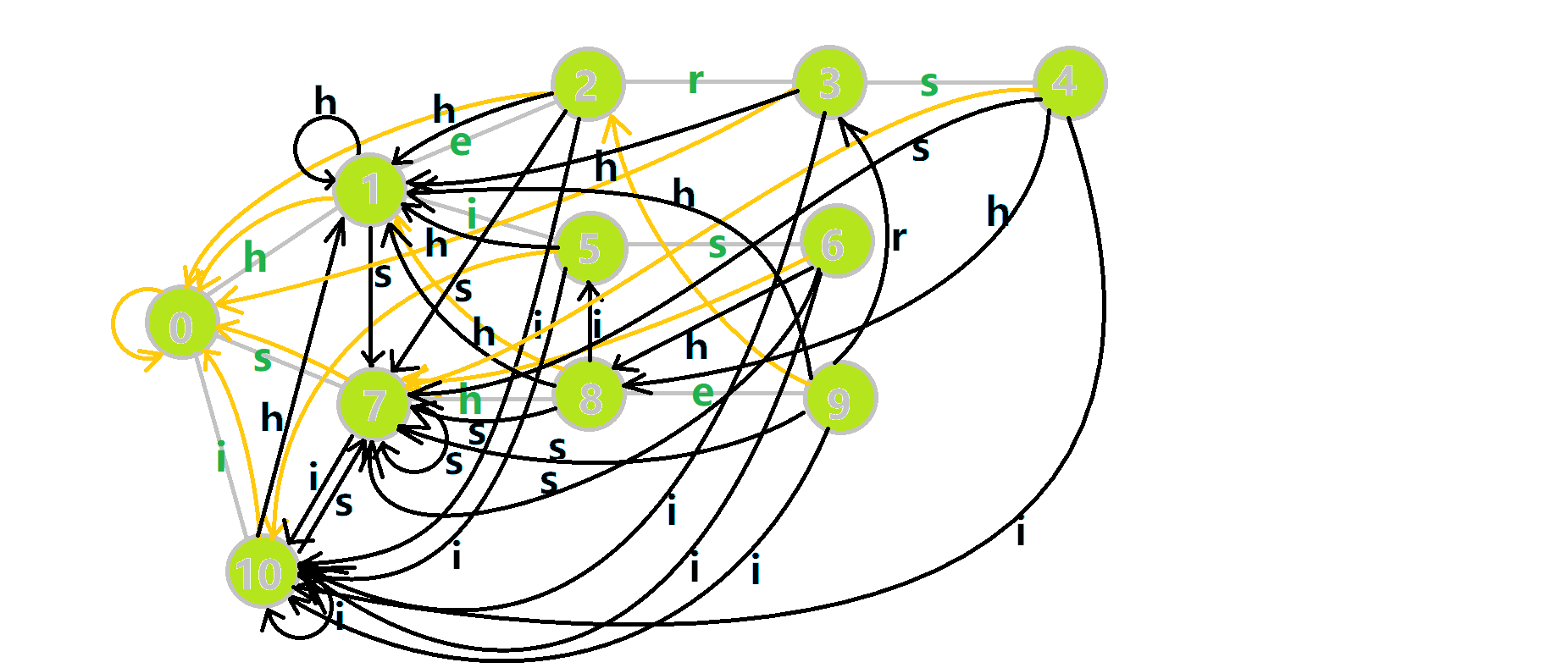
蓝色结点：BFS 遍历到的结点 u。
蓝色的边：当前结点下，AC 自动机修改字典树结构连出的边。
黑色的边：AC 自动机修改字典树结构连出的边。
红色的边：当前结点求出的 fail 指针。
黄色的边：fail 指针。
灰色的边：字典树的边。

匹配

匹配的过程就朴素一些。用u记录当前匹配到的字符。循环遍历匹配的串，同时在自动机上跳模式串。每完成一次模式串的匹配，就进行统计，并把临时维护的一些信息清零。如果失配，就沿着fail指针往回跳。如图：

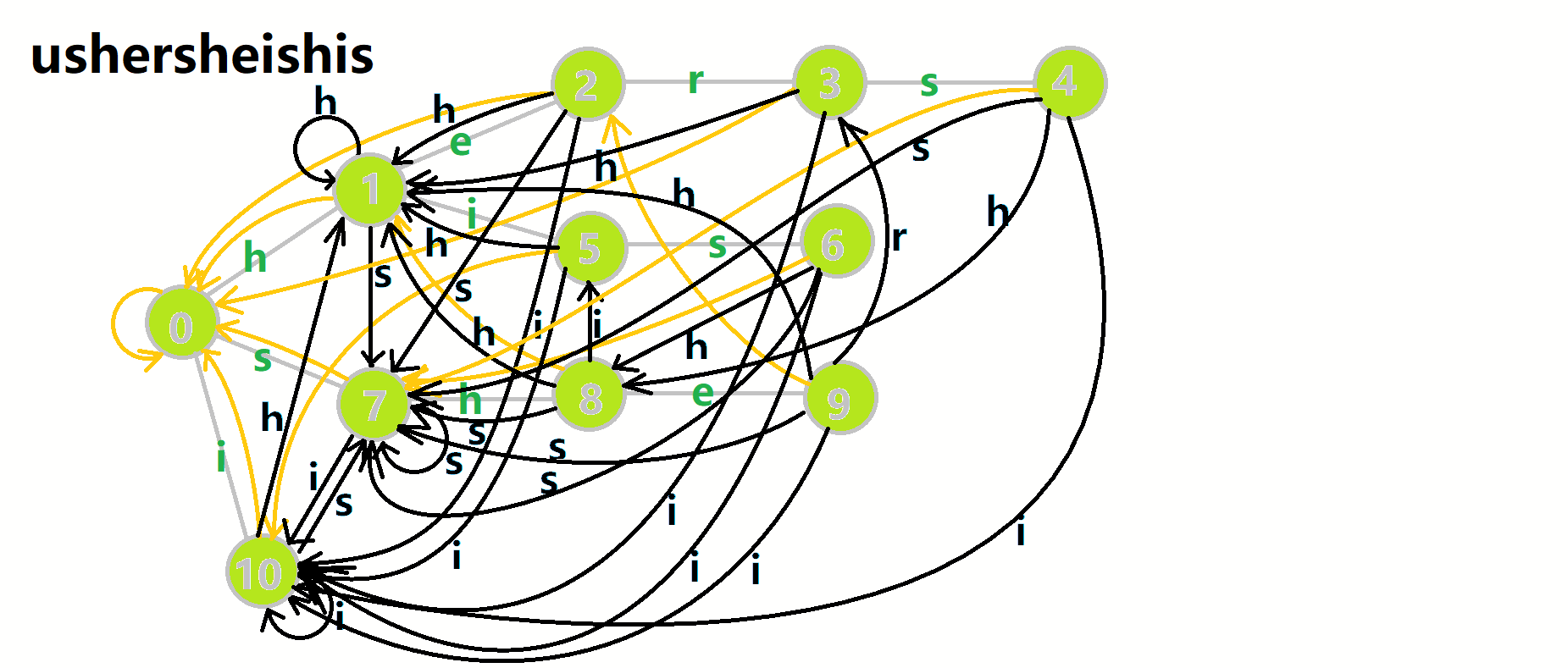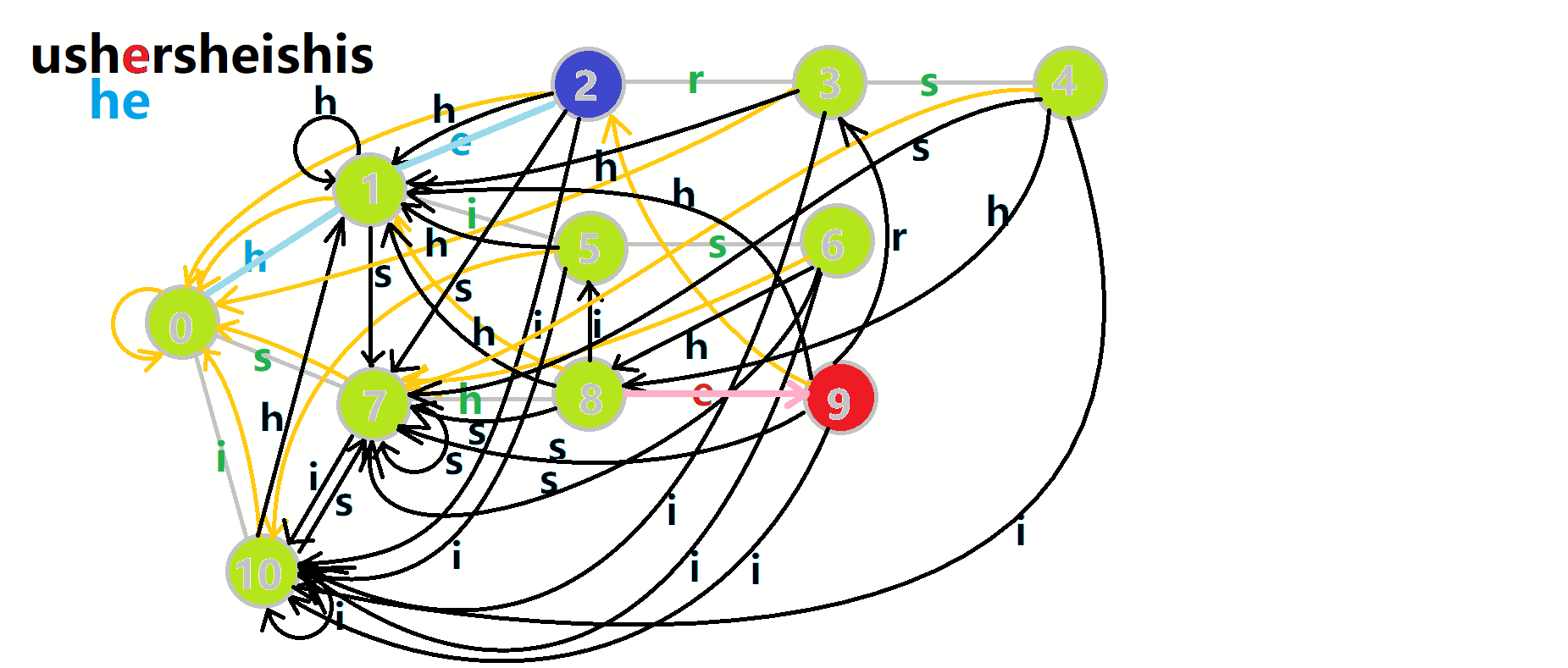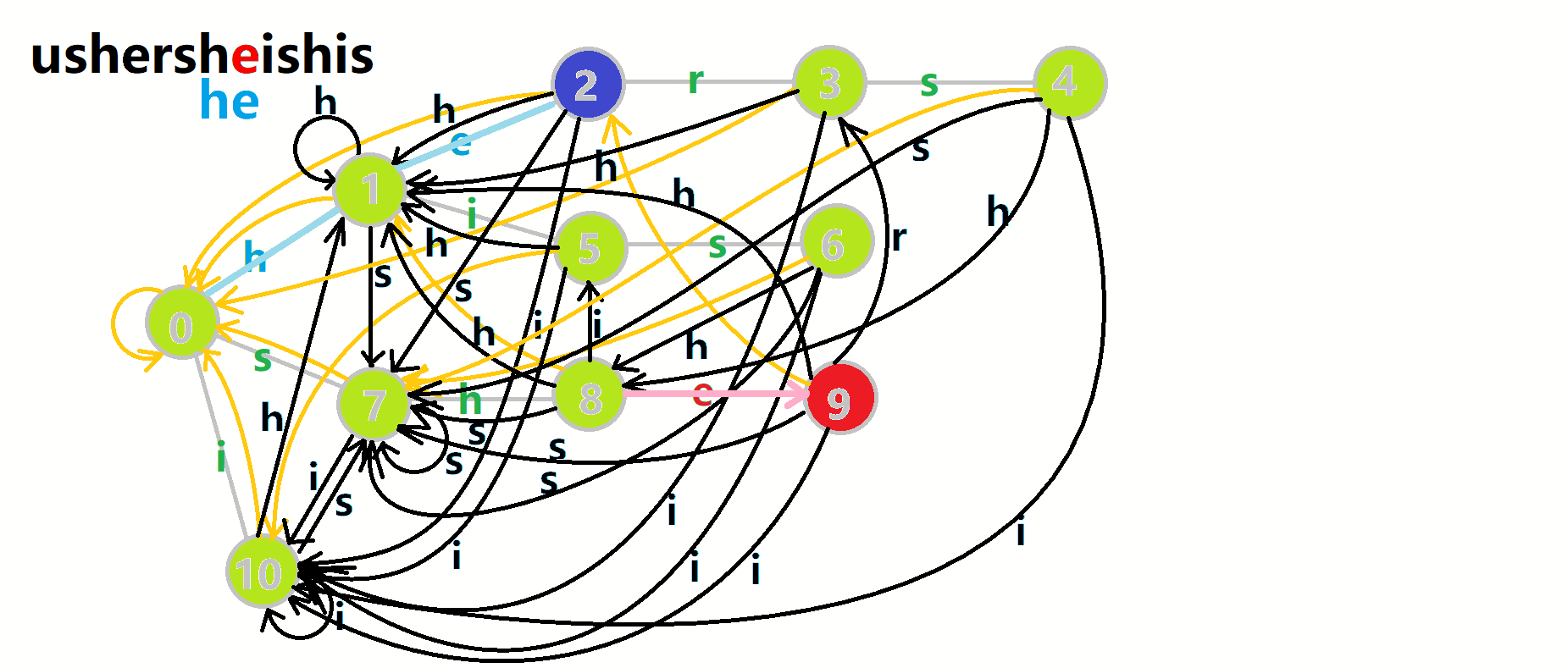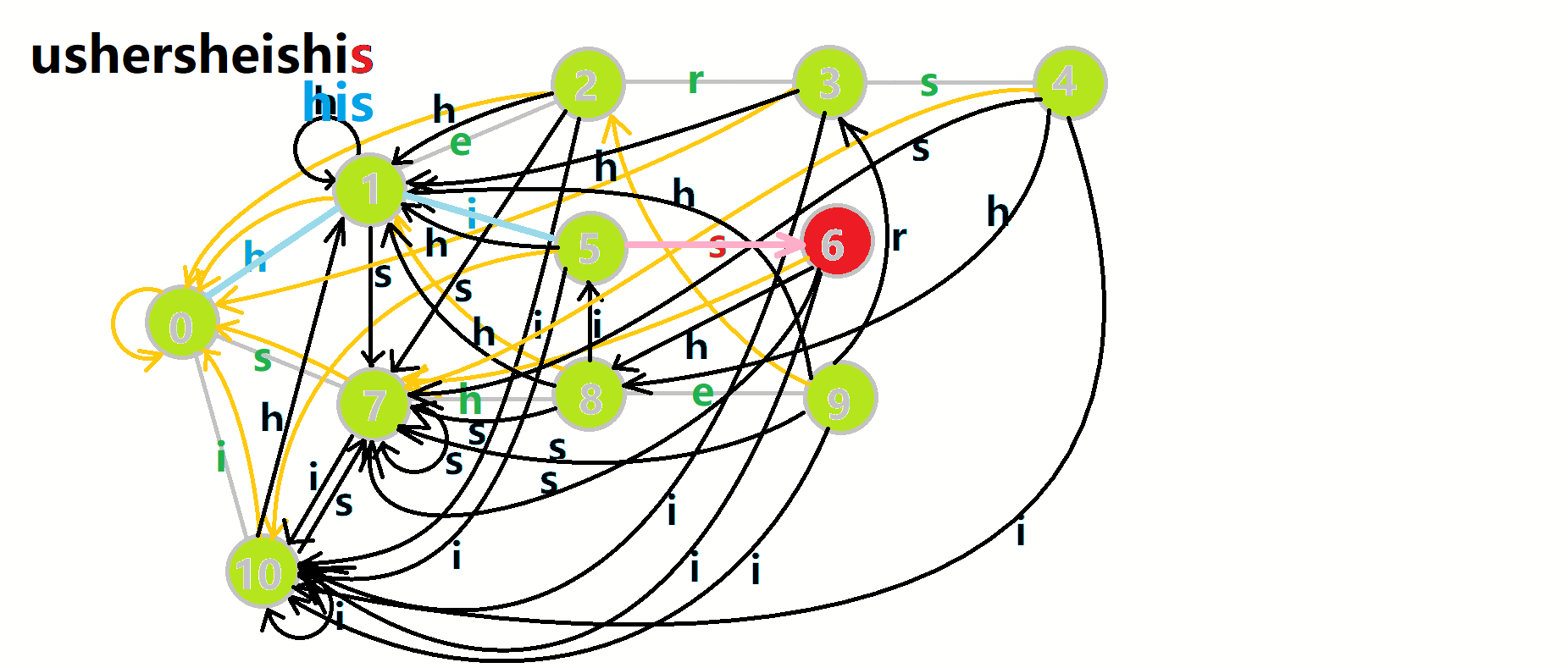
红色结点：p 结点。
粉色箭头：p 在自动机上的跳转。
蓝色的边：成功匹配的模式串。
蓝色结点：示跳 fail 指针时的结点（状态）。

效率优化

我们的 AC 自动机中，每次匹配，会一直向fail边跳来找到所有的匹配，但是这样的效率较低，在某些题目中会超时
那么需要如何优化呢？首先需要了解到fail指针的一个性质：一个AC自动机中，如果只保留fail边，那么剩余的图一定是一棵树，因为fail不会成环，且深度一定比现在低，所以得证
这样 AC 自动机的匹配就可以转化为在fail树上的链求和问题，只需要优化一下该部分就可以了
考虑利用拓扑排序进行优化，构造时提前记录好入度，查询时只为找到节点的ans打上标记，最后用拓扑排序进行统计

例题 Luogu P5357【模板】AC 自动机

囊括以上所有内容，由于数据较强需要进行效率优化。代码如下：

#include<bits/stdc++.h>
using namespace std;
#define N 200010

int n;
string s;
string t;
//trie树
struct Trie{
	int son[27];//子节点
	int cnt;//匹配计数
	int fail;//失配指针
	int indeg;//入度
	int id;//编号
	
	//节点初始化
	void init(){
		for(int i=0;i<27;i++) son[i]=0;
		cnt=fail=id=0;
	}
}trie[2000010];
int tot;//节点总数
int ans[N],pid;//答案
int idx[N];//编号

//初始化
void init(){
	tot=pid=0;
	trie[0].init();
}


//插入节点
void insert(string s,int &x){
	int u=0;//当前节点
	for(int i=0;s[i];i++){
		int &child=trie[u].son[s[i]-'a'];//下一个子节点的引用
		if(!child) {
			child=++tot;//没有就插入新节点
			trie[child].init();//初始化新节点
		}
		u=child;//继续查找下一个
	}
	//由于有可能出现相同的模式串，需要去重
	if(!trie[u].id) trie[u].id=++pid;//首次出现新增
	x=trie[u].id;//模式串编号对应节点编号
}

//求取失配指针
/*利用BFS序顺次求取失配指针，可以保证指针从上向下
逐层求取，顺序不会混乱。同时在函数中处理入度，为
拓扑排序优化查询做准备*/
void build(){
	queue<int> q;
	for(int i=0;i<26;i++){
		if(trie[0].son[i]) q.push(trie[0].son[i]);
		//初始将所有根节点入队
	}
	while(!q.empty()){
		int x=q.front();
		q.pop();
		for(int i=0;i<26;i++){
			if(trie[x].son[i]){//有一个对应i号字母的儿子
				//有儿子只用跳一次fail指针
				trie[trie[x].son[i]].fail=trie[trie[x].fail].son[i];
				//计算入度
				trie[trie[trie[x].fail].son[i]].indeg++;
				q.push(trie[x].son[i]);//加入队列
			}else{
				//没有儿子就跳到fail指针指向位置的父亲身上
				trie[x].son[i]=trie[trie[x].fail].son[i];
			}
		}
	}
}

//询问
void query(string t){
	int u=0;
	for(int i=0;s[i];i++){
		u=trie[u].son[t[i]-'a'];//转移
		trie[u].cnt++;//计数增加
	}
	//拓扑排序求解答案
	queue<int> q;
	for(int i=0;i<=tot;i++){
		if(trie[i].indeg==0) q.push(i);
		//入度为0的点入队
	}
	while(!q.empty()){
		int x=q.front();
		q.pop();
		ans[trie[x].id]=trie[x].cnt;//记录答案
		int y=trie[x].fail;//继续往失配指针上跳
		trie[y].cnt+=trie[x].cnt;
		trie[y].indeg--;
		if(!trie[y].indeg) q.push(y);//入度清零则入队
	}
}

signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	init();
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>t;
		insert(t,idx[i]);
		ans[i]=0;
	}
	build();
	cin>>s;
	query(s);
	for(int i=1;i<=n;i++){
		cout<<ans[idx[i]]<<'\n';
	}
	return 0;
}