解码排序算法

排序基础概念

排序的定义

排序是将 “无序” 的记录序列，按照数据节点的某一属性（称为 “字段”，如学生的学号、分数、商品的价格等）调整为 “有序”（升序或降序）记录序列的操作。例如：考试成绩表中，需按 “语文成绩”“总成绩” 等字段排序，才能确定学生的各科排名或综合排名。

排序的稳定性

定义：若待排序序列中存在多个 “关键字相同” 的记录（如两个学生分数都是 85 分），排序后这些记录的 “相对位置” 未发生变化，则称该排序算法是稳定的；反之则不稳定。
示例：原序列：[学生A（85分）, 学生B（90分）, 学生C（85分）]
- 稳定排序后：[学生A（85分）, 学生C（85分）, 学生B（90分）]（A 和 C 的相对位置不变）；
- 不稳定排序后：[学生C（85分）, 学生A（85分）, 学生B（90分）]（A 和 C 的相对位置改变）。
注意：若序列中所有关键字唯一（如学号），排序结果唯一，稳定性无关紧要；若关键字可重复（如分数），需根据需求选择稳定 / 不稳定算法（如排名需保留同分数学生的原始顺序，选稳定算法）。

排序算法分类及详解

根据设计思想，排序算法主要分为插入类、交换类、选择类，此外还有计数排序等特殊场景算法。

插入类排序 —— 直接插入排序

核心思想

从无序序列中逐个取出元素，插入到 “已排序序列” 的合适位置，逐步扩大已排序序列的范围，直到所有元素插入完成。

算法步骤（以升序为例，序列：[5, 3, 4, 7, 2, 8, 6, 9, 1]）

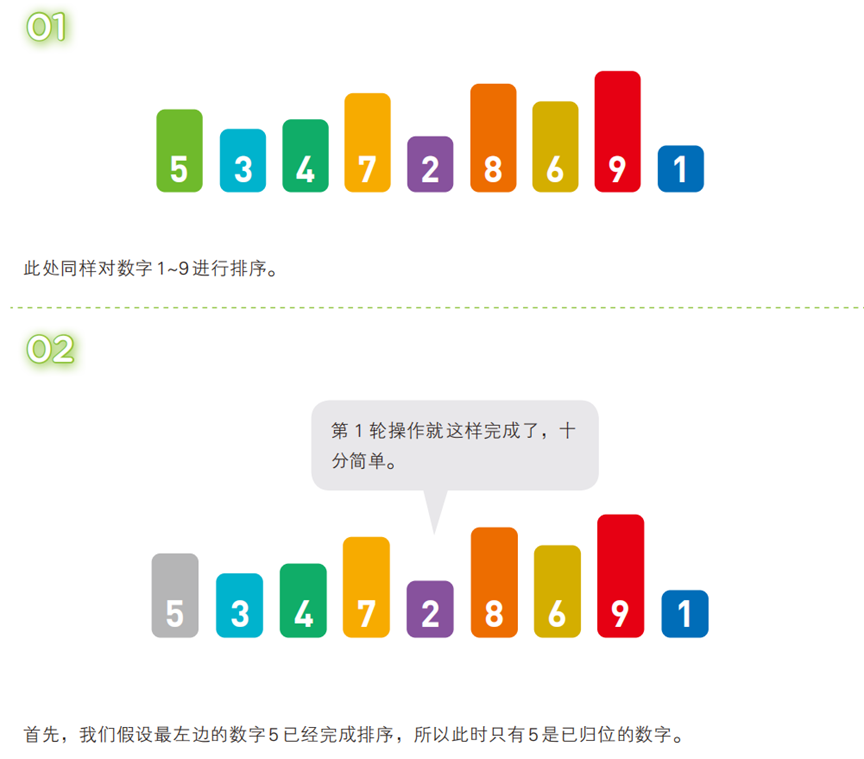
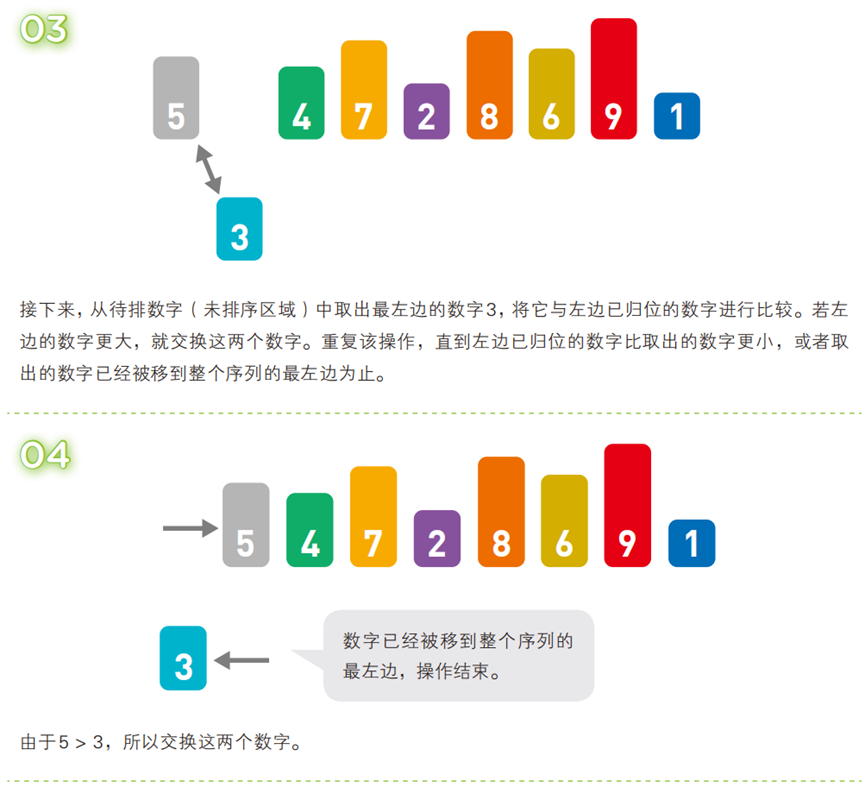
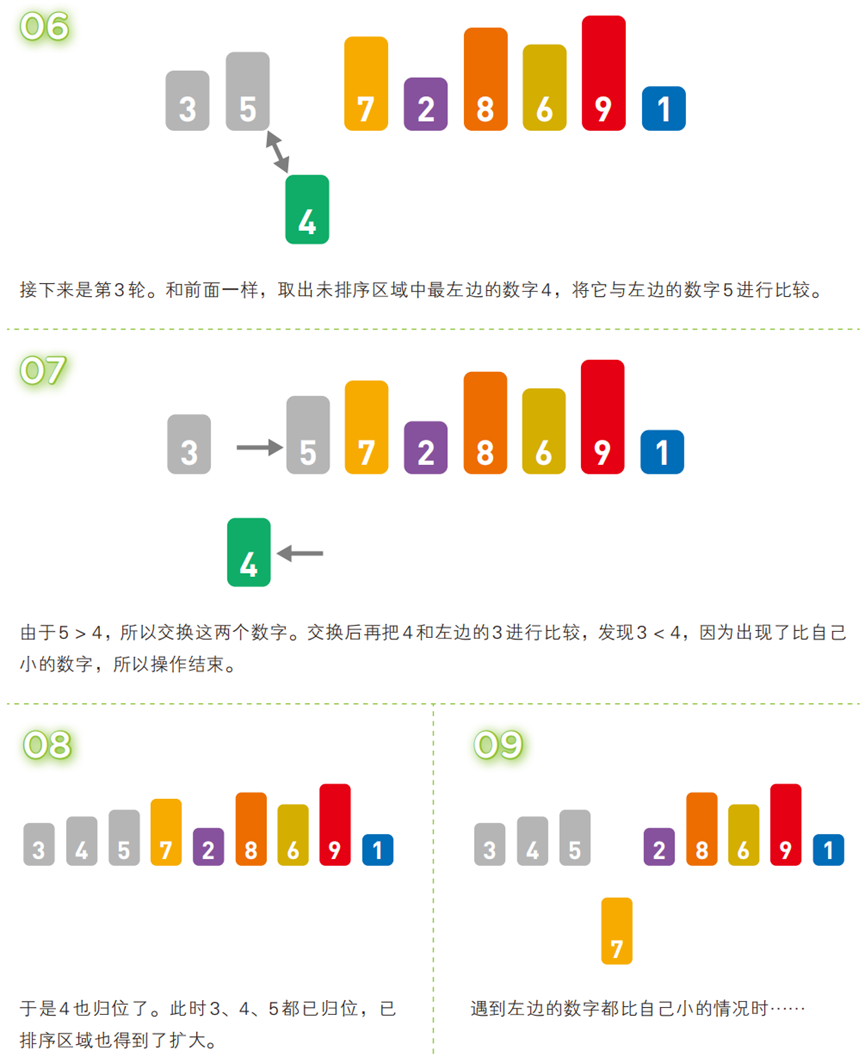
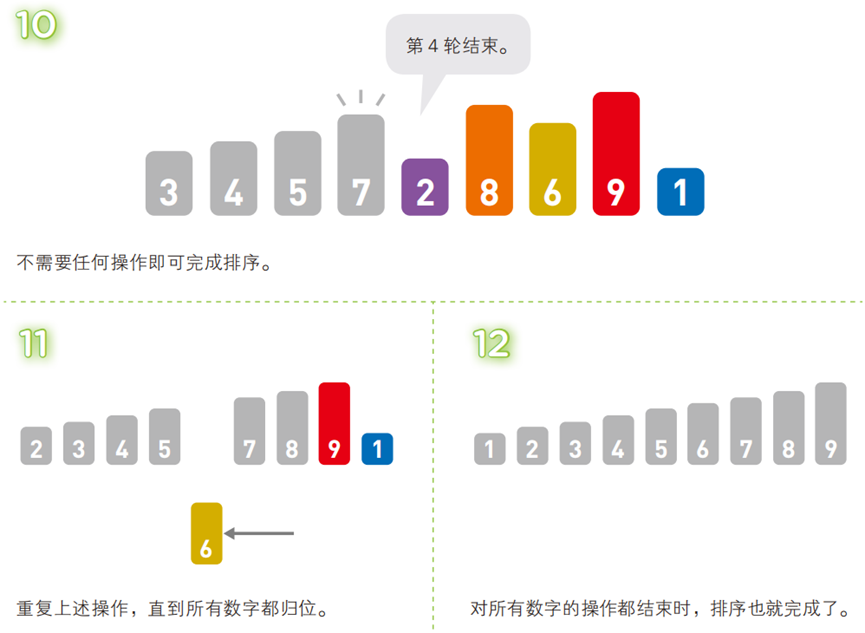
代码（C 语言）

// buf：待排序数组；bufsize：数组长度
void InsertSort(int buf[], int bufsize) {
    int temp = 0;      // 备份当前待插入元素
    int current_prev = 0; // 记录插入位置
    
    // 外层循环：遍历无序序列（从第2个元素开始，下标i=1）
    for (int i = 1; i < bufsize; ++i) {
        temp = buf[i]; // 备份待插入元素
        // 内层循环：从已排序序列尾部向前比较
        for (int j = i - 1; j >= 0; --j) {
            if (temp < buf[j]) { 
                buf[j + 1] = buf[j]; // 已排序元素后移
            } else {
                current_prev = j + 1; // 确定插入位置
                break;
            }
        }
        buf[current_prev] = temp; // 插入元素
    }
}

时间复杂度
- 最坏情况：O(n²)（序列完全逆序，每轮需比较最多次数）；
- 最优情况：O(n)（序列已有序，每轮仅需比较 1 次）；
- 适用场景：基本有序的小规模序列（如少量数据的实时排序）。
稳定性：直接插入排序是稳定的。原理：当待插入元素与已排序序列中的元素相等时，会插入到相等元素的后面（因为比较条件是temp < buf[j]，相等时不移动，直接插入到j+1位置），不会改变相等元素的相对位置。

交换类排序

交换类排序的核心是 “通过相邻元素的比较与交换，使元素逐步归位”，常见算法为冒泡排序和快速排序。

冒泡排序

核心思想

两两比较相邻元素，若顺序错误（升序中前大后小）则交换；每轮迭代后，最大（或最小）的元素会像 “泡泡” 一样浮到序列的对应位置（尾部或头部）。

算法步骤（以升序为例，序列：[5, 3, 4, 7, 2, 8, 6, 9, 1]）

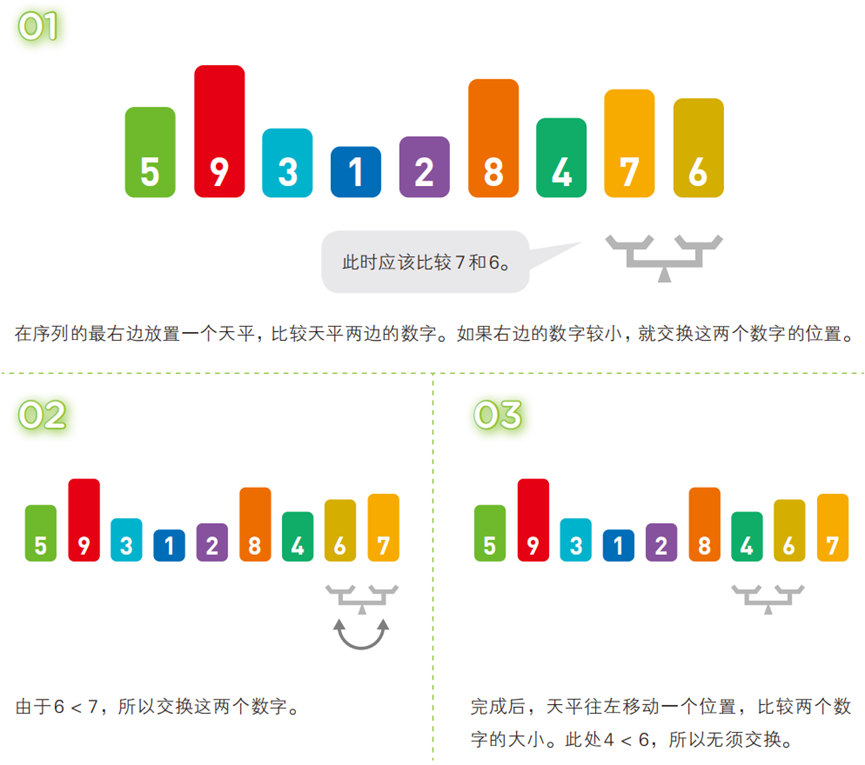
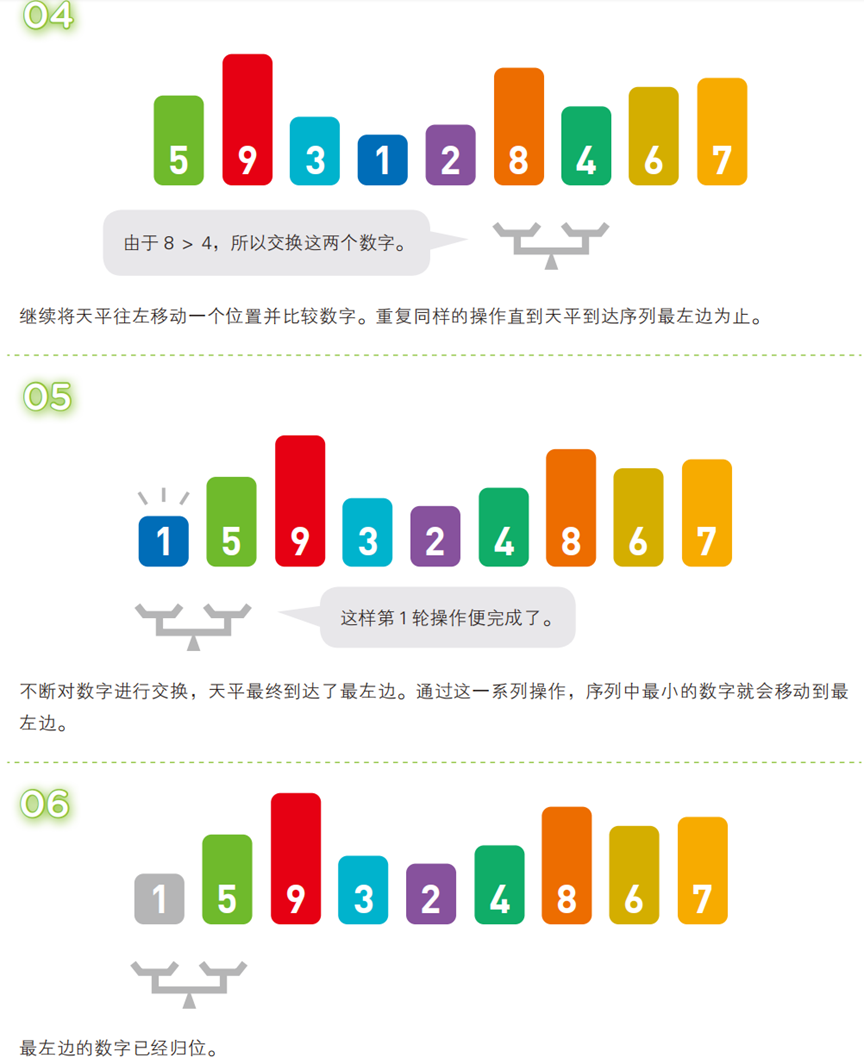
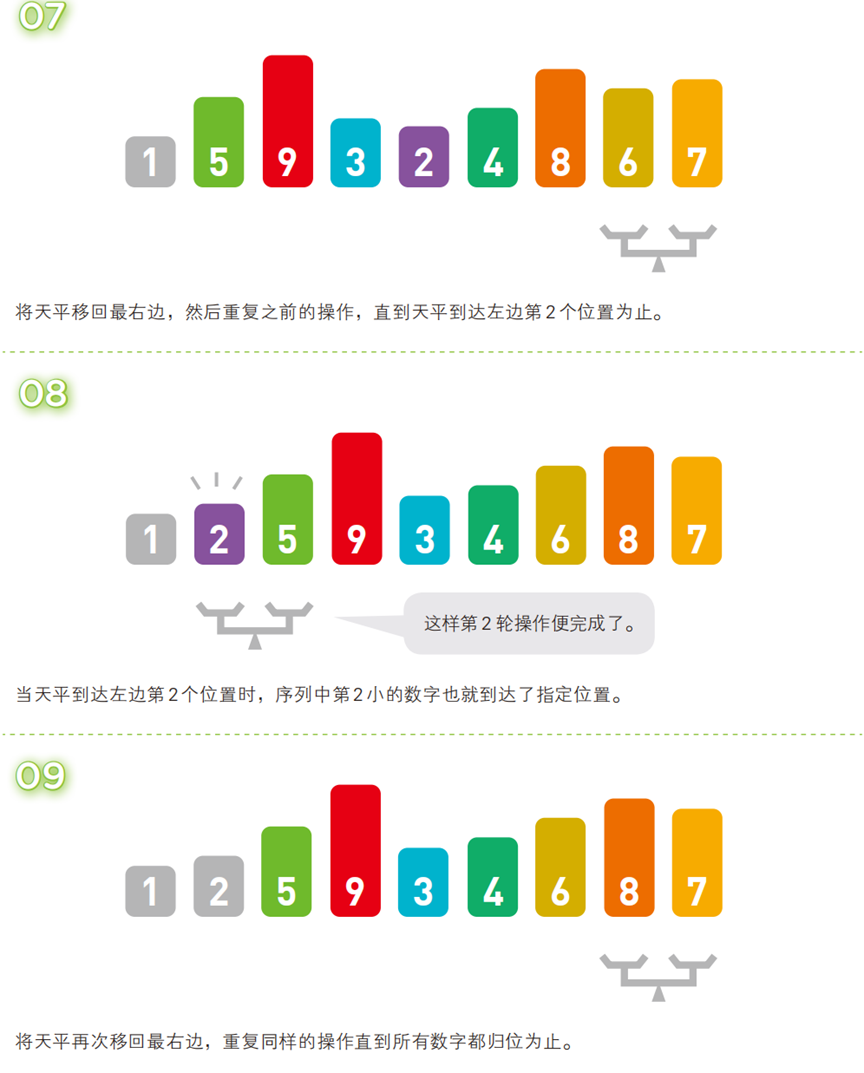
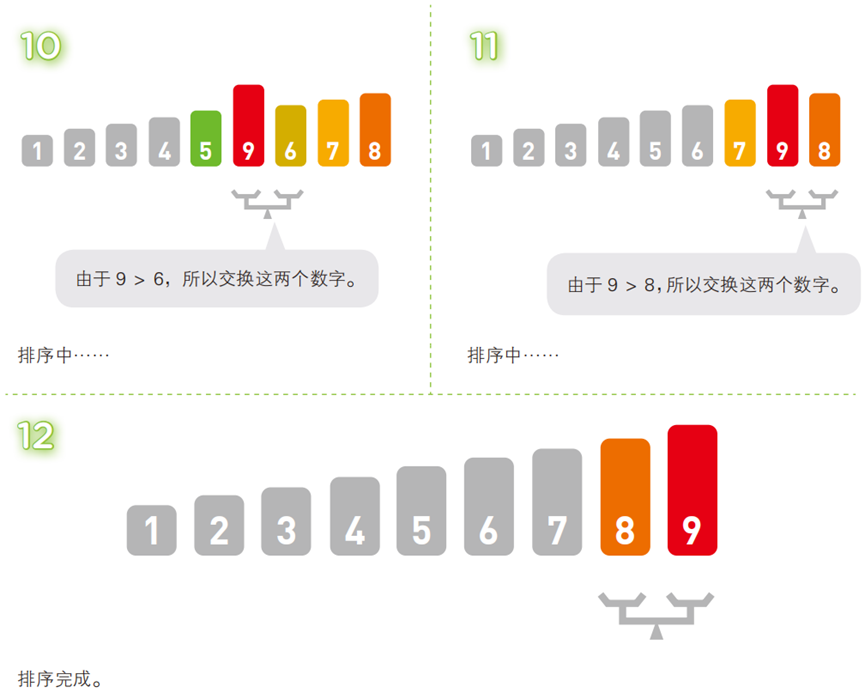
代码（C 语言）

void BubbleSort(int buf[], int bufsize) {
    int temp = 0;       // 备份交换元素
    int is_swapped = 0; // 标志位：记录本轮是否有交换（关键优化）
    
    // 外层循环：控制最大轮数（最多n-1轮）
    for (int n = 1; n < bufsize; ++n) {
        is_swapped = 0; // 每轮开始前重置标志位
        
        // 内层循环：每轮比较次数=数组长度-轮数（已归位元素无需比较）
        for (int m = 0; m < bufsize - n; ++m) {
            if (buf[m] > buf[m + 1]) { // 前大后小，交换
                temp = buf[m];
                buf[m] = buf[m + 1];
                buf[m + 1] = temp;
                is_swapped = 1; // 有交换，标志位置1
            }
        }
        
        // 若本轮无交换，说明序列已有序，直接终止排序（减少后续比较）
        if (is_swapped == 0) {
            break;
        }
    }
}

时间复杂度
- 最坏情况：O(n²)（完全逆序，需完成所有比较和交换）；
- 最优情况：O(n)（完全有序，仅需 1 轮比较）；
- 平均情况：O(n²)（大多数无序序列的表现）。

快速排序

核心思想

基于 “分治法” 和 “递归”：
- 选一个 “基准值”（通常为序列首个元素）；
- 将序列分为三部分：[比基准值小的元素] + 基准值 + [比基准值大的元素]；
- 对前后两个子序列递归执行上述步骤，直到子序列仅含 1 个元素（子序列已有序），最终整体有序。
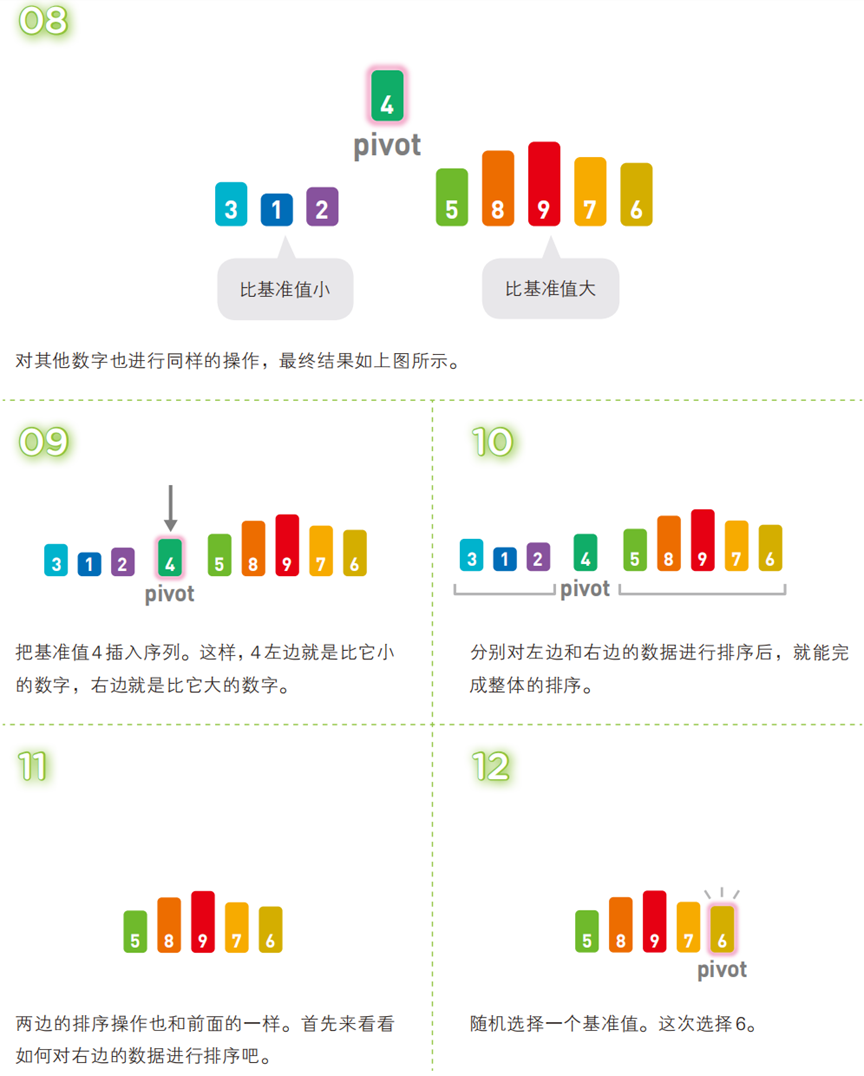
算法步骤（以升序为例，序列：[3, 5, 8, 1, 2, 9, 4, 7, 6]）

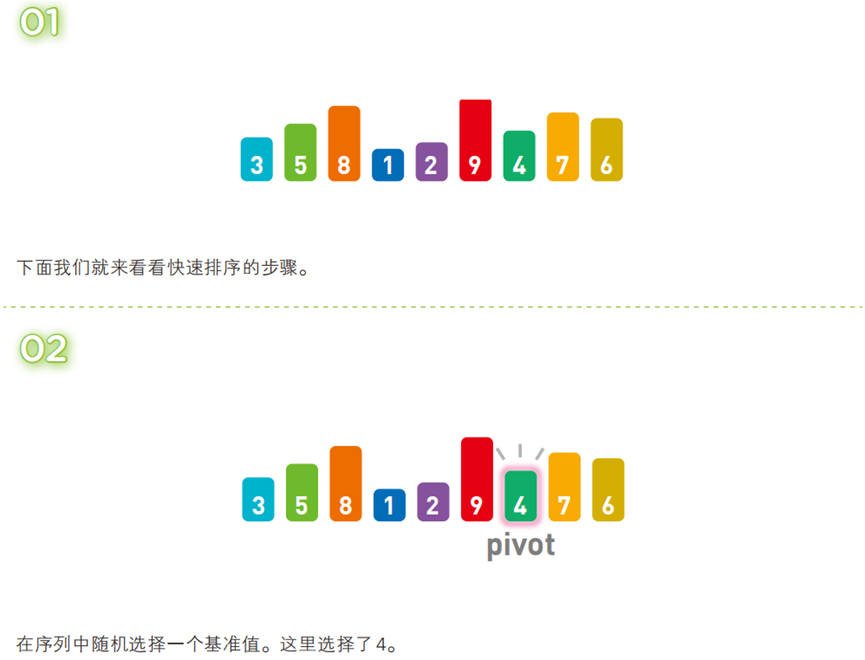
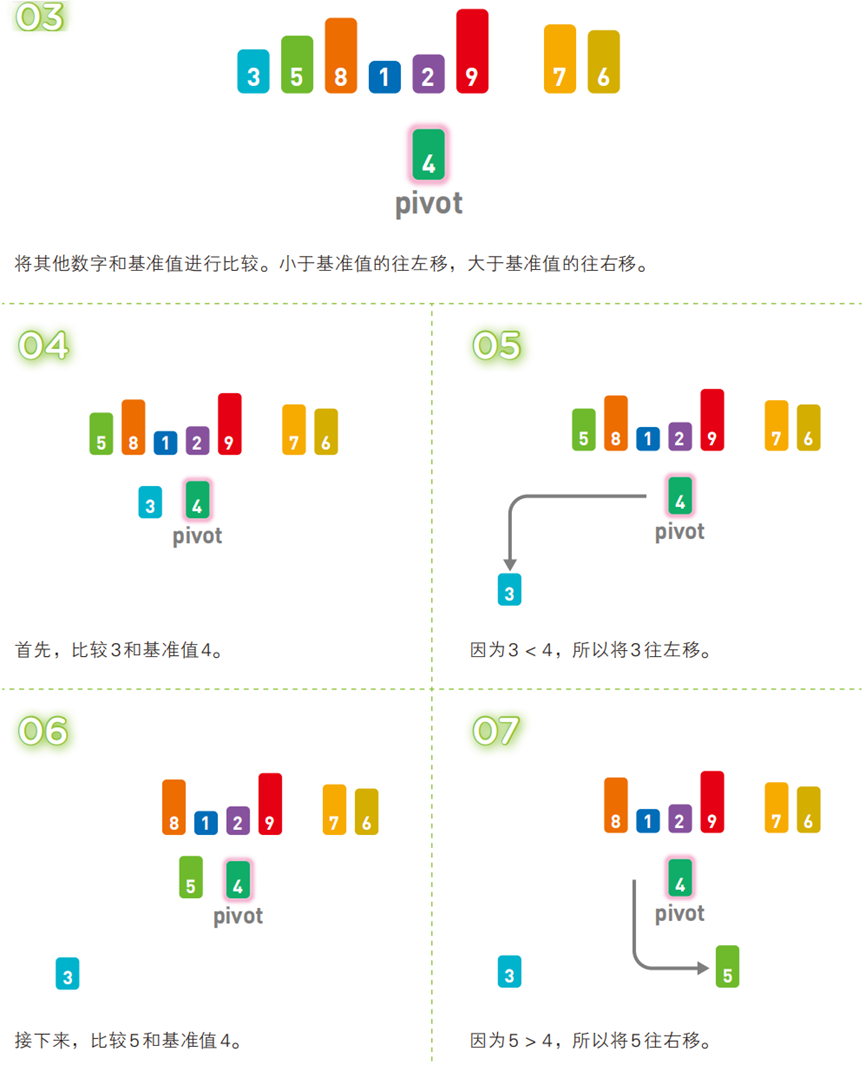
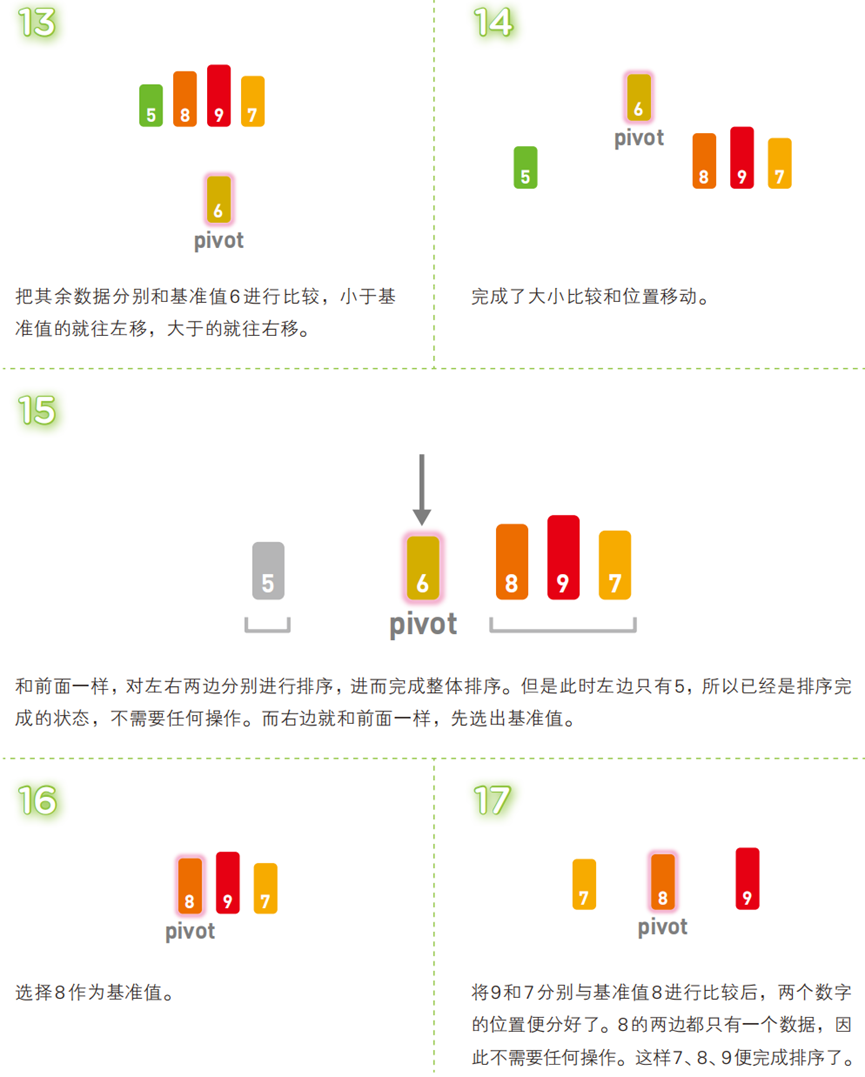
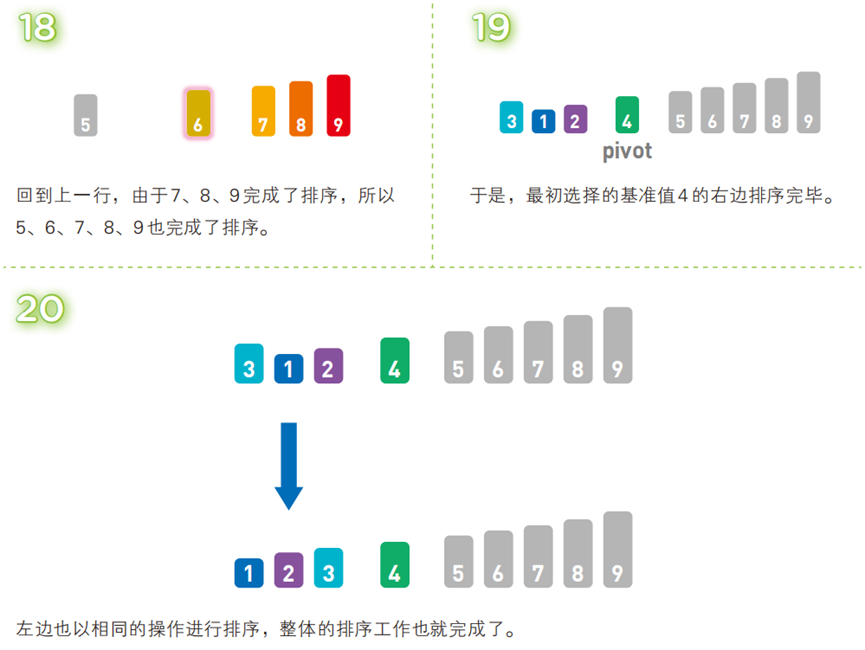
代码（C 语言）

// low：序列起始下标；high：序列末尾下标
void QuickSort(int R[], int low, int high) {
    if (low >= high) return; // 子序列仅1个元素，直接返回
    
    int i = low, j = high;
    int pivot = R[low]; // 基准值（选序列首个元素）
    
    // 调整元素位置，使基准值归位
    while (i != j) {
        // 右指针j左移：找比基准值小的元素
        while (j > i && R[j] >= pivot) --j;
        if (i < j) R[i++] = R[j]; // 赋值后i右移
        
        // 左指针i右移：找比基准值大的元素
        while (i < j && R[i] <= pivot) ++i;
        if (i < j) R[j--] = R[i]; // 赋值后j左移
    }
    R[i] = pivot; // 基准值归位到i（此时i=j）
    
    // 递归处理左子序列和右子序列
    QuickSort(R, low, i - 1);
    QuickSort(R, i + 1, high);
}

时间复杂度
- 平均情况：O(nlogn)（每轮分治排除一半数据，效率高）；
- 最坏情况：O(n²)（序列已有序，基准值每次选到最小 / 最大值，分治失效）；
- 适用场景：无序的中大规模序列（实际开发中应用最广的排序算法之一）。
稳定性：快速排序是不稳定的。原理：基准值归位时的交换操作可能导致相等元素的相对位置改变。

选择类排序 —— 选择排序

核心思想

每轮从 “无序序列” 中通过线性查找找到最小（或最大）元素，将其与 “无序序列的首位元素” 交换，使最小元素归位到已排序序列的末尾；重复n-1轮（n为序列长度）。

算法步骤（以升序为例，序列：[6, 1, 7, 8, 9, 3, 5, 4, 2]）

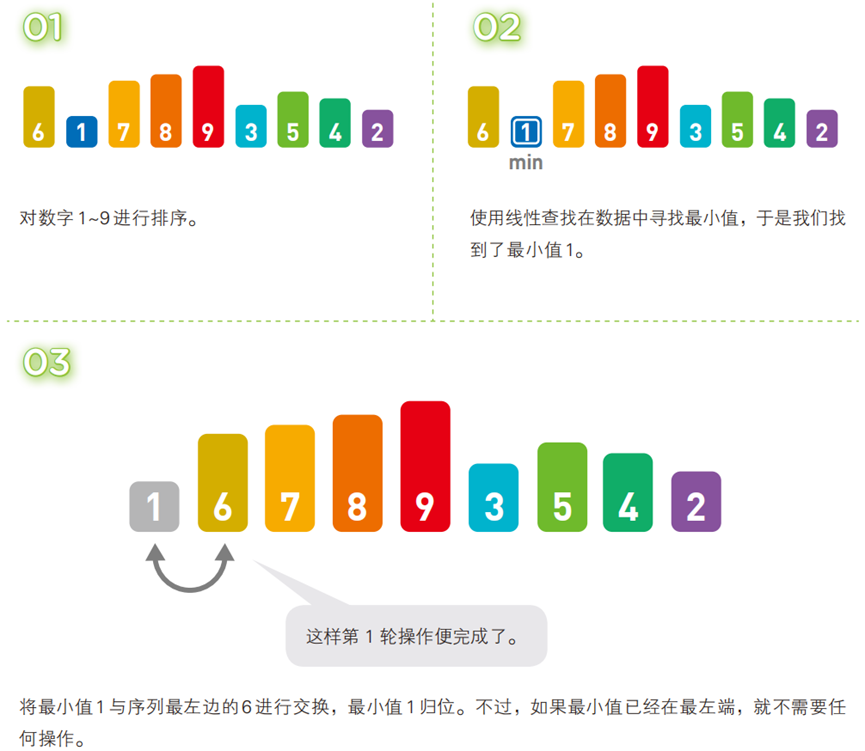
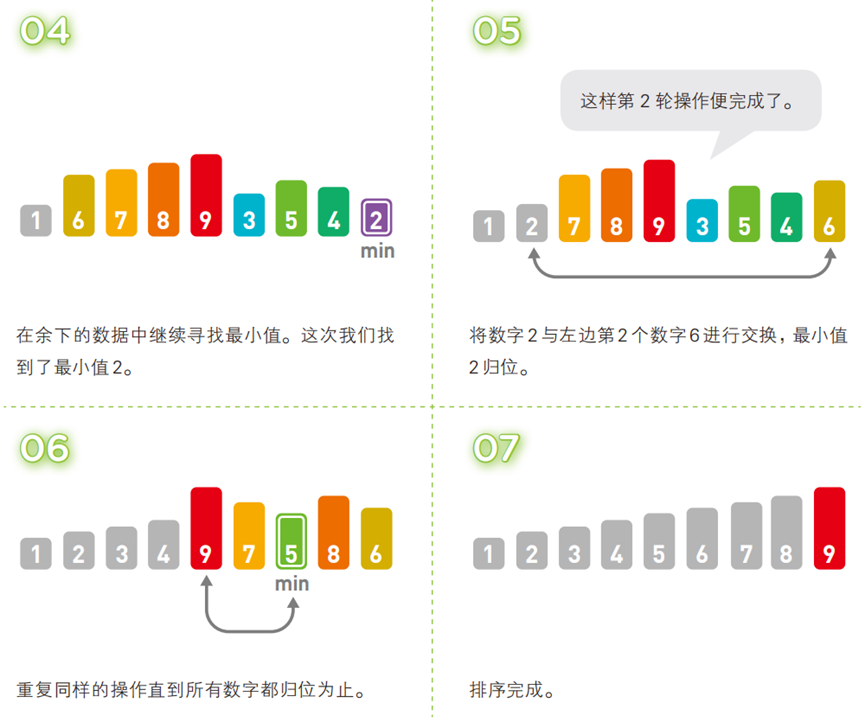
代码（C 语言）

void SelectSort(int buf[], int bufsize) {
    int min_idx = 0; // 记录无序序列中最小元素的下标
    int temp = 0;    // 备份交换元素
    
    // 外层循环：控制轮数（最多n-1轮）
    for (int n = 0; n < bufsize - 1; ++n) {
        min_idx = n; // 初始假设无序序列首位为最小元素
        // 内层循环：遍历无序序列，找真正的最小元素下标
        for (int i = n + 1; i < bufsize; ++i) {
            if (buf[i] < buf[min_idx]) {
                min_idx = i; // 更新最小元素下标
            }
        }
        // 交换：将最小元素与无序序列首位交换
        temp = buf[min_idx];
        buf[min_idx] = buf[n];
        buf[n] = temp;
    }
}

时间复杂度
- 无论序列初始状态，总比较次数为n(n-1)/2，时间复杂度O(n²)；
- 交换次数固定为n-1次（每轮最多 1 次交换）。
稳定性：选择排序是不稳定的。原理：每轮会将 “无序区最小元素” 与 “无序区首位元素” 交换，若首位元素后存在与其相等的元素，交换会破坏相对位置。

其他排序 —— 计数排序

适用场景

待排序序列的关键字为int 型，且所有关键字互不相同（如无重复的分数、ID 等）。

核心思想

对每个元素，统计 “序列中比它小的元素个数cnt”，该元素在 “有序结果数组” 中的位置即为cnt（因为有cnt个元素比它小，所以它排第cnt位）。

算法步骤（序列 A：[2, 6, 9, 7, 1, 8, 5]，结果数组 B）

遍历 A 中每个元素，统计cnt：
- 2：比它小的元素有1（cnt=1）→ B[1] = 2；
- 6：比它小的元素有1,2,5（cnt=3）→ B[3] = 6；
- 9：比它小的元素有1,2,5,6,7,8（cnt=6）→ B[6] = 9；
- 依次统计其他元素，最终 B 为[1, 2, 5, 6, 7, 8, 9]。
代码（C 语言）

// A：待排序数组；B：结果数组；size：数组长度
void CountSort(int A[], int B[], int size) {
    int cnt = 0; // 统计比当前元素小的个数
    
    // 外层循环：遍历待排序数组A
    for (int n = 0; n < size; ++n) {
        cnt = 0; // 每次统计前重置计数器
        // 内层循环：统计比A[n]小的元素个数
        for (int i = 0; i < size; ++i) {
            if (A[i] < A[n]) {
                cnt++;
            }
        }
        B[cnt] = A[n]; // 插入到结果数组的对应位置
    }
}

排序测试辅助 —— 随机数生成

排序算法测试时，常需生成随机整数序列，可通过 C 语言的rand()和srand()函数实现：

核心函数

srand(unsigned int seed)：初始化随机数种子（若不初始化，每次运行生成的随机数序列相同）；
- 通常用time(NULL)作为种子（time(NULL)返回当前系统时间的秒数，确保每次种子不同）；
rand()：生成0~RAND_MAX（通常为32767）的随机整数。

生成指定范围的随机数

若需生成[0, k-1]范围的随机数，用rand() % k（取余运算）；例：生成0~99的随机数：rand() % 100。

代码示例（生成 10 个 0~99 的随机数）

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main() {
    int i;
    srand(time(NULL)); // 初始化随机数种子（仅需1次）
    
    // 生成10个0~99的随机数并输出
    for (i = 0; i < 10; ++i) {
        printf("%d ", rand() % 100);
    }
    printf("\n");
    return 0;
}

posted @ 2025-10-05 19:28 YouEmbedded 阅读(2) 评论(0) 收藏举报

刷新页面返回顶部

YouEmbedded