解码数据结构队列

队列的基础原理

核心定义与原则

本质：队列（Queue）是线性结构，与栈同属线性存储，核心差异在于操作原则：
- 栈遵循 “后进先出（LIFO）”，仅允许一端操作；
- 队列遵循 “先进先出（FIFO，First Input First Output)”，需在两端操作且权限分离
类比：队列可理解为 “水管”—— 数据从 “进水口”（队尾）流入，从 “出水口”（队头）流出，先流入的数据先流出。

关键术语与操作

术语	定义与操作权限
队头（Front/Head）	队列 “出口”，仅允许删除元素，对应操作 “出队（Dequeue）”。
队尾（Rear/Tail）	队列 “入口”，仅允许插入元素，对应操作 “入队（Enqueue）”。
空队列	无元素状态，出队前需判空（空队列无法出队）。
满队列	元素达最大容量（仅数组实现需判满，链表无固定容量），入队前需判满（满队列无法入队）。

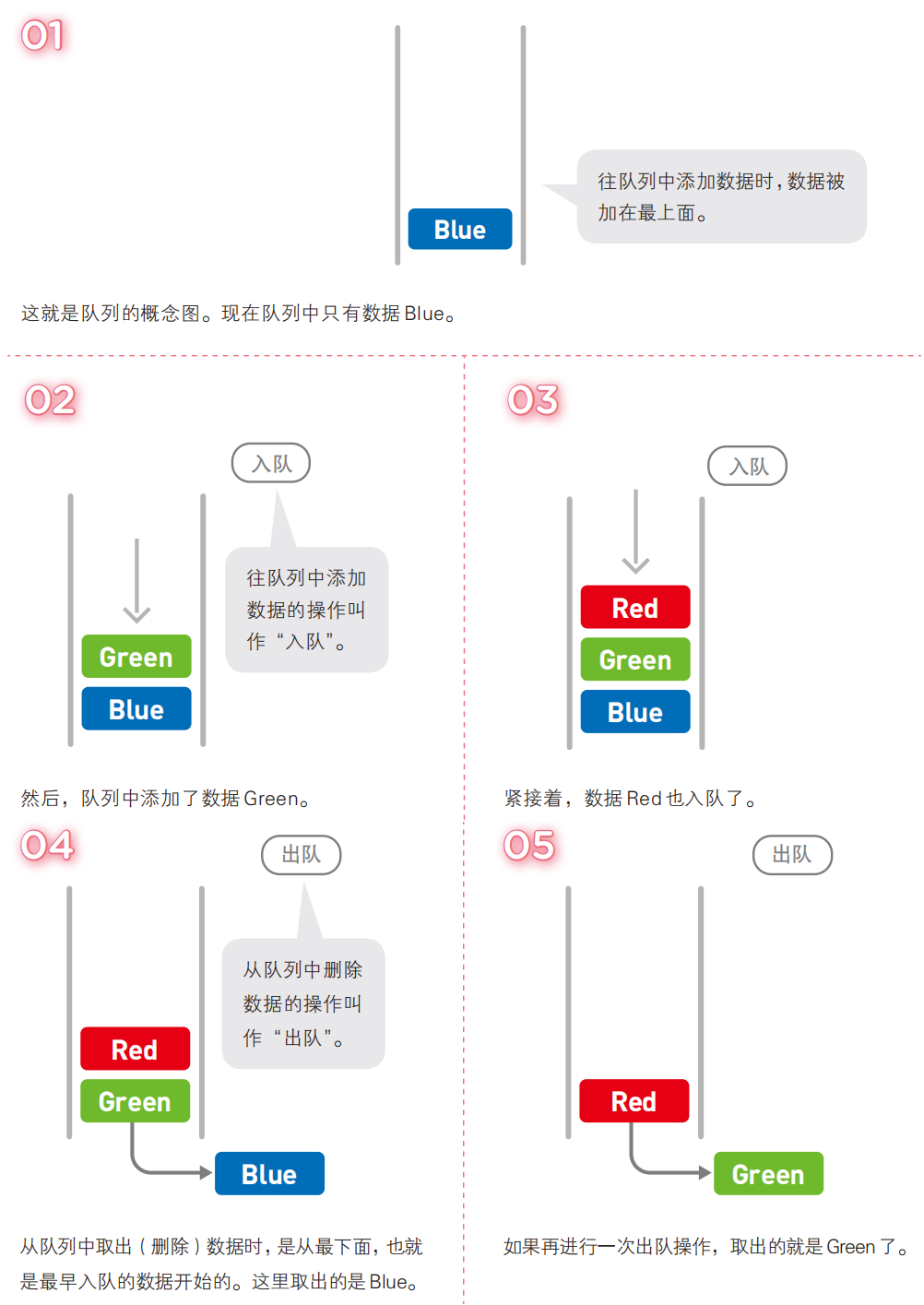
操作流程示例

以 “Blue→Green→Red” 入队出队为例：

出队入队

基于数组的实现

普通数组队列

核心问题：出队需移动所有后续元素，时间复杂度 O (n)，效率低。

结构定义：

typedef int DataType_t; // 元素类型（默认int，可自定义）
typedef struct ArrayQueue {
    DataType_t *Addr;    // 存储元素的数组首地址
    unsigned int Size;   // 数组总容量（队列最大元素数）
    int Front;           // 队头下标（指向当前队头元素）
    int Rear;            // 队尾下标（指向待插入位置）
    int Count;           // 元素个数（辅助判空/判满）
} ArrQueue_t;

核心操作（“出队移元素” 逻辑）：
- 初始化：申请内存，Front=0、Rear=0、Count=0；
- 入队：满队则拒，否则Rear位置存元素，Rear++、Count++（O(1)）；
- 出队：空队则拒，否则取Front元素，后续元素整体前移 1 位，Rear--、Count--（O (n)）；
- 判空 / 判满：空队→Count==0；满队→Count>=Size。

代码(参考，不常用)

// 创建并初始化普通数组队列
ArrQueue_t *ArrQueue_Create(unsigned int size) {
    // 申请管理结构体内存
    ArrQueue_t *Manager = (ArrQueue_t *)calloc(1, sizeof(ArrQueue_t));
    if (NULL == Manager) {
        perror("calloc memory for ArrayQueue manager is failed");
        exit(-1); // 程序异常终止
    }

    // 申请元素存储数组内存
    Manager->Addr = (DataType_t *)calloc(size, sizeof(DataType_t));
    if (NULL == Manager->Addr) {
        perror("calloc memory for ArrayQueue element array is failed");
        free(Manager); // 避免内存泄漏
        exit(-1);
    }

    // 初始化队列参数
    Manager->Size = size;
    Manager->Front = 0;
    Manager->Rear = 0;
    Manager->Count = 0;

    return Manager;
}

// 判空
bool ArrQueue_IsEmpty(ArrQueue_t *Manager) {
    if (NULL == Manager) {
        printf("ArrayQueue manager is invalid!\n");
        return true; // 视为逻辑空，避免错误操作
    }
    return (Manager->Count == 0) ? true : false;
}

// 判满
bool ArrQueue_IsFull(ArrQueue_t *Manager) {
    if (NULL == Manager) {
        printf("ArrayQueue manager is invalid!\n");
        return true; // 视为逻辑满，避免错误操作
    }
    return (Manager->Count >= Manager->Size) ? true : false;
}

// 入队
bool ArrQueue_Enqueue(ArrQueue_t *Manager, DataType_t Data) {
    if (NULL == Manager) {
        printf("ArrayQueue manager is invalid!\n");
        return false;
    }
    if (ArrQueue_IsFull(Manager)) {
        printf("ArrayQueue is Full!\n");
        return false;
    }

    // 队尾插入元素，更新Rear和Count
    Manager->Addr[Manager->Rear] = Data;
    Manager->Rear++;
    Manager->Count++;

    return true;
}

// 出队（出队需移动元素）
bool ArrQueue_Dequeue(ArrQueue_t *Manager, DataType_t *OutData) {
    if (NULL == Manager || NULL == OutData) {
        printf("ArrayQueue manager or OutData is invalid!\n");
        return false;
    }
    if (ArrQueue_IsEmpty(Manager)) {
        printf("ArrayQueue is Empty!\n");
        return false;
    }

    // 取出队头元素
    *OutData = Manager->Addr[Manager->Front];

    // 关键：移动所有后继元素
    for (int i = Manager->Front; i < Manager->Rear - 1; i++) {
        Manager->Addr[i] = Manager->Addr[i + 1];
    }

    // 更新队尾和元素个数
    Manager->Rear--;
    Manager->Count--;

    return true;
}

// 销毁
void ArrQueue_Destroy(ArrQueue_t **Manager) { // 二级指针：接收“指针的地址”
    if (NULL == Manager || NULL == *Manager) return;

    free((*Manager)->Addr); // 先释放元素数组
    free(*Manager);         // 再释放管理结构体
    *Manager = NULL;        // 关键：将外部的指针变量置为 NULL，彻底避免野指针
}

缺陷：出队效率低。

循环队列

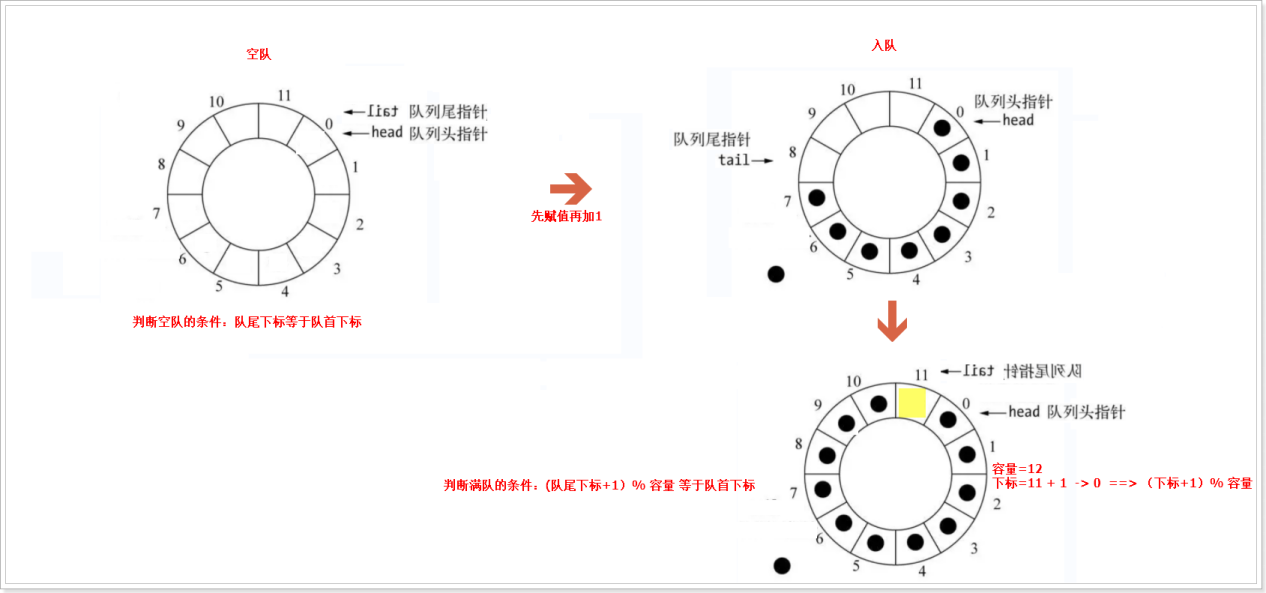
为解决普通数组队列缺陷，引入循环队列（环形缓冲区），通过 “模运算” 实现下标循环复用。

数组循环队列

结构定义：

typedef struct CircularQueue {
    DataType_t *Addr;    // 堆内存首地址（存储元素）
    unsigned int Size;   // 队列容量（数组大小）
    int Rear;            // 队尾下标（指向待插入位置的前一个元素）
    int Front;           // 队首下标（指向当前队头元素）
} CirQueue_t;

核心操作：

创建与初始化：

CirQueue_t *CirQueue_Create(unsigned int size) {
    // 申请管理结构体内存
    CirQueue_t *Manager = (CirQueue_t *)calloc(1, sizeof(CirQueue_t));
    if (NULL == Manager) {
        perror("calloc memory for CircularQueue manager is failed");
        exit(-1);
    }

    // 申请元素存储数组内存（容量为size）
    Manager->Addr = (DataType_t *)calloc(size, sizeof(DataType_t));
    if (NULL == Manager->Addr) {
        perror("calloc memory for CircularQueue element is failed");
        free(Manager); // 释放已申请的管理结构体，避免泄漏
        exit(-1);
    }

    // 初始化队列参数（空队时Rear=Front=0）
    Manager->Size = size;
    Manager->Rear = 0;
    Manager->Front = 0;

    return Manager;
}

判空 / 判满：

空队：Manager->Front == Manager->Rear；
满队：(Manager->Rear + 1) % Manager->Size == Manager->Front（浪费 1 个空间，避免空满混淆）；

bool CirQueue_IsEmpty(CirQueue_t *M) { return M->Front == M->Rear; }
bool CirQueue_IsFull(CirQueue_t *M) { return (M->Rear+1)%M->Size == M->Front; }

入队

bool CirQueue_Enqueue(CirQueue_t *Manager, DataType_t Data) {
    if (NULL == Manager) {
        printf("CircularQueue manager is invalid!\n");
        return false;
    }
    // 先判满，满队无法入队
    if (CirQueue_IsFull(Manager)) {
        printf("CircularQueue is Full!\n");
        return false;
    }

    // 队尾插入元素（Rear指向待插入位置）
    Manager->Addr[Manager->Rear] = Data;
    // 模运算更新Rear，避免下标越界
    Manager->Rear = (Manager->Rear + 1) % Manager->Size;

    return true;
}

出队

bool CirQueue_Dequeue(CirQueue_t *Manager, DataType_t *OutData) {
    if (NULL == Manager || NULL == OutData) {
        printf("CircularQueue manager or OutData is invalid!\n");
        return false;
    }
    // 先判空，空队无法出队
    if (CirQueue_IsEmpty(Manager)) {
        printf("CircularQueue is Empty!\n");
        return false;
    }

    // 取出队头元素（Front指向当前队头）
    *OutData = Manager->Addr[Manager->Front];
    // 模运算更新Front，无需移动元素
    Manager->Front = (Manager->Front + 1) % Manager->Size;

    return true;

销毁

void CirQueue_Destroy(CirQueue_t **Manager) {
    if (NULL == Manager || NULL == *Manager) return;

    free((*Manager)->Addr); // 释放元素数组
    free(*Manager);         // 释放管理结构体
    *Manager = NULL;        // 关键：将外部的指针变量置为 NULL，避免野指针
}

优势：出队 O (1)、空间复用、空满区分清晰。

基于链表的实现

“链表实现队列可避免内存浪费与元素移动”，核心是 “头删（出队）、尾插（入队）”

链式队列

基础链式队列

结构定义（逻辑推导）：

// 链表节点
typedef struct QueueNode {
    DataType_t Data;          // 存储元素
    struct QueueNode *Next;   // 指向下一节点
} QueueNode_t;

// 管理结构体
typedef struct LinkQueue {
    QueueNode_t *Front; // 队头指针（头删位置）
    QueueNode_t *Rear;  // 队尾指针（尾插位置）
} LinkQueue_t;

核心操作（“头删尾插” 逻辑）：
- 初始化：Front=NULL、Rear=NULL（空队）；
- 入队：新节点接队尾，空队则头 / 队尾均指向新节点（O (1)）；
- 出队：删除队头节点，仅 1 个元素则头 / 队尾置 NULL（O (1)）；
- 判空：return Front == NULL）。

代码

// 创建并初始化链式队列
LinkQueue_t *LinkQueue_Create() {
    // 申请管理结构体内存
    LinkQueue_t *Queue = (LinkQueue_t *)calloc(1, sizeof(LinkQueue_t));
    if (NULL == Queue) {
        perror("calloc memory for LinkQueue manager is failed");
        exit(-1);
    }

    // 空队时，队头、队尾均指向NULL
    Queue->Front = NULL;
    Queue->Rear = NULL;

    return Queue;
}

// 判空
bool LinkQueue_IsEmpty(LinkQueue_t *Queue) {
    if (NULL == Queue) {
        printf("LinkQueue manager is invalid!\n");
        return true;
    }
    return (NULL == Queue->Front) ? true : false;
}

// 入队
bool LinkQueue_Enqueue(LinkQueue_t *Queue, DataType_t Data) {
    if (NULL == Queue) {
        printf("LinkQueue manager is invalid!\n");
        return false;
    }

    // 创建新节点（存储待入队元素）
    QueueNode_t *NewNode = (QueueNode_t *)calloc(1, sizeof(QueueNode_t));
    if (NULL == NewNode) {
        perror("calloc memory for LinkQueue node is failed");
        return false;
    }
    NewNode->Data = Data;
    NewNode->Next = NULL; // 尾节点Next必须为NULL（避免链表断裂）

    // 分情况插入队尾
    if (LinkQueue_IsEmpty(Queue)) {
        // 空队：队头、队尾均指向新节点
        Queue->Front = NewNode;
        Queue->Rear = NewNode;
    } else {
        // 非空队：新节点接在队尾后，更新Rear
        Queue->Rear->Next = NewNode;
        Queue->Rear = NewNode;
    }

    return true;
}

// 出队
bool LinkQueue_Dequeue(LinkQueue_t *Queue, DataType_t *OutData) {
    if (NULL == Queue || NULL == OutData) {
        printf("LinkQueue manager or OutData is invalid!\n");
        return false;
    }
    if (LinkQueue_IsEmpty(Queue)) {
        printf("LinkQueue is Empty!\n");
        return false;
    }

    // 保存待删除的队头节点（避免删除后无法访问）
    QueueNode_t *DelNode = Queue->Front;
    *OutData = DelNode->Data; // 传出出队元素

    // 分情况更新队头
    if (Queue->Front == Queue->Rear) {
        // 仅1个元素：出队后为空队，队头、队尾均置NULL
        Queue->Front = NULL;
        Queue->Rear = NULL;
    } else {
        // 多个元素：队头后移到下一个节点
        Queue->Front = Queue->Front->Next;
    }

    // 释放被删除节点的内存
    free(DelNode);
    DelNode = NULL;

    return true;
}

// 销毁
void LinkQueue_Destroy(LinkQueue_t **Queue) { // 二级指针：接收外部指针的地址
    if (NULL == Queue || NULL == *Queue) return;

    // 先遍历释放所有节点（和原来逻辑一致）
    QueueNode_t *CurrNode = (*Queue)->Front;
    while (NULL != CurrNode) {
        QueueNode_t *TempNode = CurrNode;
        CurrNode = CurrNode->Next;
        free(TempNode);
    }

    // 释放管理结构体
    free(*Queue); 
    *Queue = NULL; // 关键：将外部的指针变量置为 NULL，彻底避免野指针
}

优势：动态扩容、无元素移动、无空间浪费。

链式循环队列（基于链表逻辑的优化延伸）

为满足基础链式队列的‘循环访问’需求（如轮询场景），在保留‘头删（出队）尾插（入队）’核心逻辑的基础上，补充环形结构（队尾Next指向队头），实现遍历到队尾后直接回连队头的循环访问能力。

结构定义：

typedef struct CirQueueNode {
    DataType_t Data;            // 存储元素
    struct CirQueueNode *Next;  // 指向下一节点（队尾Next指向队头）
} CirQueueNode_t;

typedef struct CircularLinkQueue {
    CirQueueNode_t *Front; // 队头指针（头删位置）
    CirQueueNode_t *Rear;  // 队尾指针（尾插位置）
} CirLinkQueue_t;

核心操作（遵循 “头删尾插” 逻辑）：

初始化（带头节点，简化判空）：

CirLinkQueue_t *CirLinkQueue_Create() {
    // 申请管理结构体内存
    CirLinkQueue_t *Queue = (CirLinkQueue_t *)calloc(1, sizeof(CirLinkQueue_t));
    if (NULL == Queue) {
        perror("calloc memory for CircularLinkQueue manager is failed");
        exit(-1);
    }

    // 创建头节点（空节点，Next指向自身，形成初始环）
    CirQueueNode_t *HeadNode = (CirQueueNode_t *)calloc(1, sizeof(CirQueueNode_t));
    if (NULL == HeadNode) {
        perror("calloc memory for CircularLinkQueue head node is failed");
        free(Queue);
        exit(-1);
    }
    HeadNode->Next = HeadNode; // 初始环：头节点Next指向自己

    // 空队时，队头、队尾均指向头节点（简化判空）
    Queue->Front = HeadNode;
    Queue->Rear = HeadNode;

    return Queue;
}

判空：

bool CirLinkQueue_IsEmpty(CirLinkQueue_t *Queue) {
    if (NULL == Queue) {
        printf("CircularLinkQueue manager is invalid!\n");
        return true;
    }
    // 空队：队头、队尾均指向头节点（Front==Rear）
    return (Queue->Front == Queue->Rear) ? true : false;
}

入队（尾插 + 保持环形）：

bool CirLinkQueue_Enqueue(CirLinkQueue_t *Queue, DataType_t Data) {
    if (NULL == Queue) {
        printf("CircularLinkQueue manager is invalid!\n");
        return false;
    }

    // 创建新节点
    CirQueueNode_t *NewNode = (CirQueueNode_t *)calloc(1, sizeof(CirQueueNode_t));
    if (NULL == NewNode) {
        perror("calloc memory for CircularLinkQueue node is failed");
        return false;
    }
    NewNode->Data = Data;
    NewNode->Next = Queue->Front; // 新节点Next指向队头（保持环形）

    // 尾插：更新队尾指针
    Queue->Rear->Next = NewNode;
    Queue->Rear = NewNode;

    return true;
}

出队（头删 + 保持环形）：

bool CirLinkQueue_Dequeue(CirLinkQueue_t *Queue, DataType_t *OutData) {
    if (NULL == Queue || NULL == OutData) {
        printf("CircularLinkQueue manager or OutData is invalid!\n");
        return false;
    }
    if (CirLinkQueue_IsEmpty(Queue)) {
        printf("CircularLinkQueue is Empty!\n");
        return false;
    }

    // 待删除节点：头节点的后继（头节点不存储元素）
    CirQueueNode_t *DelNode = Queue->Front->Next;
    *OutData = DelNode->Data; // 传出出队元素

    // 头删：更新头节点的Next，保持环形
    Queue->Front->Next = DelNode->Next;
    // 若删除的是最后一个元素，更新Rear为Front（空队状态）
    if (Queue->Rear == DelNode) {
        Queue->Rear = Queue->Front;
    }

    // 释放被删除节点的内存
    free(DelNode);
    DelNode = NULL;

    return true;
}

销毁

void CirLinkQueue_Destroy(CirLinkQueue_t **Queue) { // 二级指针：接收外部指针的地址
    // 先判断“二级指针本身”和“外部指针指向的管理结构体”是否有效
    if (NULL == Queue || NULL == *Queue) {
        printf("CirLinkQueue manager is invalid!\n");
        return;
    }

    // 遍历删除所有环形节点（逻辑不变，仅将Queue改为(*Queue)）
    CirQueueNode_t *CurrNode = (*Queue)->Front; // 从队头开始遍历
    while (NULL != CurrNode) {
        CirQueueNode_t *TempNode = CurrNode;    // 保存当前节点，避免free后丢失指针
        CurrNode = CurrNode->Next;              // 先移动指针，再判断是否循环到起点
        
        // 环形终止条件：当前节点的下一个节点回到队头（避免死循环）
        if (CurrNode == (*Queue)->Front) {
            free(TempNode);
            break; // 删完最后一个节点，退出循环
        }
        free(TempNode);
    }

    // 释放管理结构体，并用二级指针将外部指针置为NULL
    free(*Queue);   // 释放管理结构体内存
    *Queue = NULL;  // 关键：直接修改外部指针变量，使其指向NULL，彻底避免野指针
}

优化点（基于逻辑的延伸）：判空简单、遍历高效，仍保持“头删尾插” 核心操作。

双栈实现队列

代码框架，用两个栈分工：

栈 s1：入队缓存（新元素优先压入）；
栈 s2：出队缓存（s2 空则将 s1 元素 “倒栈”，弹入 s2）。

栈操作：

// 栈的结构定义（支撑双栈模拟队列）
typedef struct Stack {
    DataType_t *Data;    // 栈元素数组
    int Top;             // 栈顶下标（-1表示空栈）
    unsigned int MaxSize;// 栈最大容量
} Stack_t;

// 创建并初始化栈
Stack_t *Stack_Create(unsigned int MaxSize) {
    Stack_t *S = (Stack_t *)calloc(1, sizeof(Stack_t));
    if (NULL == S) {
        perror("calloc memory for Stack is failed");
        exit(-1);
    }

    S->Data = (DataType_t *)calloc(MaxSize, sizeof(DataType_t));
    if (NULL == S->Data) {
        perror("calloc memory for Stack element is failed");
        free(S);
        exit(-1);
    }

    S->Top = -1;         // 空栈：栈顶为-1
    S->MaxSize = MaxSize;

    return S;
}

// 栈判空
bool Stack_IsEmpty(Stack_t *S) {
    if (NULL == S) {
        printf("Stack is invalid!\n");
        return true;
    }
    return (S->Top == -1) ? true : false;
}

// 压栈
bool Stack_Push(Stack_t *S, DataType_t Data) {
    if (NULL == S) {
        printf("Stack is invalid!\n");
        return false;
    }
    // 栈满判断
    if (S->Top >= (int)S->MaxSize - 1) {
        printf("Stack is Full!\n");
        return false;
    }

    S->Data[++S->Top] = Data; // 栈顶上移，压入元素
    return true;
}

// 弹栈
bool Stack_Pop(Stack_t *S, DataType_t *OutData) {
    if (NULL == S || NULL == OutData) {
        printf("Stack or OutData is invalid!\n");
        return false;
    }
    if (Stack_IsEmpty(S)) {
        printf("Stack is Empty!\n");
        return false;
    }

    *OutData = S->Data[S->Top--]; // 弹出栈顶元素，栈顶下移
    return true;
}
// 栈销毁（二级指针：避免外部指针成为野指针）
void Stack_Destroy(Stack_t **S) {
    if (NULL == S || NULL == *S) {  // 先判断二级指针本身和外部指针是否有效
        printf("Stack is invalid!\n");
        return;
    }

    free((*S)->Data);  // 释放栈元素数组（解引用二级指针访问成员）
    free(*S);          // 释放栈管理结构体
    *S = NULL;         // 关键：将外部的栈指针变量置为NULL，彻底避免野指针
}

双栈队列的结构体定义

用管理结构体封装两个栈（s1 入队、s2 出队），并记录队列最大容量（避免超出存储限制）：

// 数据类型定义（与栈的DataType_t保持一致，可按需修改）
typedef int DataType_t;

// 双栈队列管理结构体
typedef struct DoubleStackQueue {
    Stack_t *s1; // 入队缓存栈：新元素优先压入s1
    Stack_t *s2; // 出队缓存栈：s2空时，将s1元素"倒栈"到s2
    unsigned int MaxCapacity; // 队列最大容量（=s1.MaxSize = s2.MaxSize，避免超界）
} DSQueue_t;

创建并初始化双栈队列

创建队列时，需分别初始化 s1 和 s2（容量一致，总容量即队列最大容量）：

// 创建双栈队列（参数：队列最大容量）
DSQueue_t *DSQueue_Create(unsigned int MaxCapacity) {
    // 申请队列管理结构体内存
    DSQueue_t *queue = (DSQueue_t *)calloc(1, sizeof(DSQueue_t));
    if (NULL == queue) {
        perror("calloc memory for DoubleStackQueue failed");
        exit(-1);
    }

    // 创建s1和s2（容量均为MaxCapacity，确保队列总容量可控）
    queue->s1 = Stack_Create(MaxCapacity);
    queue->s2 = Stack_Create(MaxCapacity);
    if (NULL == queue->s1 || NULL == queue->s2) {
        perror("create s1 or s2 failed");
        // 若创建失败，释放已申请的资源，避免内存泄漏
        if (queue->s1) Stack_Destroy(&queue->s1);
        if (queue->s2) Stack_Destroy(&queue->s2);
        exit(-1);
    }

    // 初始化队列最大容量
    queue->MaxCapacity = MaxCapacity;

    return queue;
}

队列判空（核心：s1 和 s2 均为空）

队列无元素的唯一条件：入队栈 s1 和出队栈 s2 都为空（无任何可出队元素）：

// 双栈队列判空
bool DSQueue_IsEmpty(DSQueue_t *queue) {
    if (NULL == queue) {
        printf("DoubleStackQueue is invalid!\n");
        return true;
    }
    // 队列空 = s1空 且 s2空
    return (Stack_IsEmpty(queue->s1) && Stack_IsEmpty(queue->s2)) ? true : false;
}

队列判满（核心：s1 满且 s2 非空）

队列无法入队的条件：s1 已满且 s2 非空（此时 s1 的元素无法倒入 s2，无多余空间）：

// 双栈队列判满
bool DSQueue_IsFull(DSQueue_t *queue) {
    if (NULL == queue) {
        printf("DoubleStackQueue is invalid!\n");
        return true;
    }
    // 队列满 = s1满 且 s2非空（s1满但s2空时，可倒栈后继续入队）
    return (!Stack_IsEmpty(queue->s2) && (queue->s1->Top >= (int)queue->s1->MaxSize - 1)) ? true : false;
}

入队操作（核心：压入 s1，必要时倒栈）

新元素先压入 s1；若 s1 满但 s2 空，先将 s1 所有元素 “倒” 到 s2，再压入新元素：

// 双栈队列入队（参数：队列、待入队元素）
bool DSQueue_Enqueue(DSQueue_t *queue, DataType_t data) {
    if (NULL == queue) {
        printf("DoubleStackQueue is invalid!\n");
        return false;
    }
    // 先判断队列是否已满
    if (DSQueue_IsFull(queue)) {
        printf("DoubleStackQueue is Full! Enqueue failed.\n");
        return false;
    }

    // 关键：若s1满但s2空，先将s1元素倒到s2，腾出s1空间
    if (queue->s1->Top >= (int)queue->s1->MaxSize - 1 && Stack_IsEmpty(queue->s2)) {
        DataType_t temp;
        // 循环弹出s1元素，压入s2（倒栈）
        while (!Stack_IsEmpty(queue->s1)) {
            Stack_Pop(queue->s1, &temp);
            Stack_Push(queue->s2, temp);
        }
    }

    // 压入新元素到s1（入队完成）
    return Stack_Push(queue->s1, data);
}

出队操作（核心：从 s2 弹出，必要时倒栈）

优先从 s2 弹出元素；若 s2 空，先将 s1 所有元素 “倒” 到 s2，再从 s2 弹出（遵循队列 FIFO）：

// 双栈队列出队（参数：队列、传出出队元素的指针）
bool DSQueue_Dequeue(DSQueue_t *queue, DataType_t *outData) {
    if (NULL == queue || NULL == outData) {
        printf("DoubleStackQueue or outData is invalid!\n");
        return false;
    }
    // 先判断队列是否为空
    if (DSQueue_IsEmpty(queue)) {
        printf("DoubleStackQueue is Empty! Dequeue failed.\n");
        return false;
    }

    // 关键：若s2空，先将s1所有元素倒到s2，确保s2有元素可出队
    if (Stack_IsEmpty(queue->s2)) {
        DataType_t temp;
        // 循环弹出s1元素，压入s2（倒栈）
        while (!Stack_IsEmpty(queue->s1)) {
            Stack_Pop(queue->s1, &temp);
            Stack_Push(queue->s2, temp);
        }
    }

    // 从s2弹出元素（出队完成，符合FIFO）
    return Stack_Pop(queue->s2, outData);
}

队列销毁（核心：先销毁 s1/s2，再销毁管理结构体）

需用二级指针避免野指针，与你之前栈 / 队列的销毁逻辑保持一致：

// 双栈队列的销毁函数
void DSQueue_Destroy(DSQueue_t **queue) {
    if (NULL == queue || NULL == *queue) { // 检查队列指针有效性
        printf("DoubleStackQueue is invalid!\n");
        return;
    }

    // 先销毁入队栈s1
    Stack_Destroy(&(*queue)->s1);  // &(*queue)->s1 等价于取s1指针的地址
    // 再销毁出队栈s2（同理）
    Stack_Destroy(&(*queue)->s2);

    // 最后释放队列管理结构体，并将外部队列指针置空
    free(*queue);
    *queue = NULL; // 确保外部队列指针不再是野指针
}

核心逻辑总结（双栈模拟队列的关键）

操作	核心逻辑
入队	新元素压入 s1；s1 满且 s2 空时，将 s1 元素倒栈到 s2，再压入新元素。
出队	优先从 s2 弹出；s2 空时，将 s1 所有元素倒栈到 s2，再从 s2 弹出（保证 FIFO）。
判空	s1 和 s2 均为空 → 队列无元素。
判满	s1 满且 s2 非空 → 无法倒栈，无多余空间。

五种队列实现的对比

实现方式	核心特点	优势	劣势	适用场景
普通数组队列	出队移元素（O (n)），空间浪费	实现简单	效率低、空间利用率低	元素少、出队少的简单场景
数组循环队列	模运算循环，出队 O (1)，浪费 1 个空间	效率高、缓存好	固定容量	已知容量、高频操作（如 IO 缓冲区）
基础链式队列	头删尾插（O (1)），动态扩容	无空间浪费、容量灵活	遍历效率低	容量不确定（如任务队列）
链式循环队列	环形结构，Front==Rear 判空，头删尾插	判空简单、遍历高效	实现略复杂	需频繁遍历的场景（如环形调度）
双栈实现队列	s1 入队、s2 出队，依赖栈 LIFO	复用栈实现	需维护两个栈	已有栈，临时需队列功能

队列的应用场景（基于FIFO 特性）

基于 “FIFO 原则” 补充典型场景：

数据缓冲：打印机队列 —— 任务按顺序入队，打印机从队头处理；
顺序调度：银行叫号 —— 客户按取号顺序入队，窗口从队头叫号；
广度优先搜索（BFS）：树层序遍历 —— 节点按层级入队，符合 FIFO；
IO 交互：键盘缓冲区 —— 输入字符按顺序入队，程序从队头读取。

posted @ 2025-09-29 18:39 YouEmbedded 阅读(8) 评论(0) 收藏举报

刷新页面返回顶部

YouEmbedded

解码数据结构队列

队列的基础原理

核心定义与原则

关键术语与操作

操作流程示例

基于数组的实现

普通数组队列

循环队列

基于链表的实现

基础链式队列

链式循环队列（基于链表逻辑的优化延伸）

双栈实现队列

五种队列实现的对比

队列的应用场景（基于FIFO 特性）

公告