解码数据结构线性表之链表

概念

链表的定义

链表是一种线性数据结构，由一系列节点组成，节点之间通过指针连接，形成链式结构。每个节点包含数据域和指针域，数据域存储数据，指针域指向其他节点。

与数组不同，链表的节点在内存中不需要连续存储，通过指针维系节点间的逻辑关系，这使得链表在插入和删除操作上更具灵活性。

核心术语辨析

术语	定义	特点
头指针（Head Pointer）	指向链表第一个节点（可能是头节点或首节点）的指针	是访问链表的入口，空链表时为 NULL
头节点（Head Node）	位于链表起始位置的特殊节点，不存储有效数据	可选节点，用于简化边界操作，统一链表操作逻辑
首节点（First Node）	链表中第一个存储有效数据的节点	非空链表必有，若有头节点则首节点是头节点的后继
尾节点（Last Node）	链表中最后一个存储有效数据的节点	非空链表必有，普通链表中尾节点的后继为 NULL
节点（Node）	链表的基本组成单位	包含数据域和指针域

操作流程示例

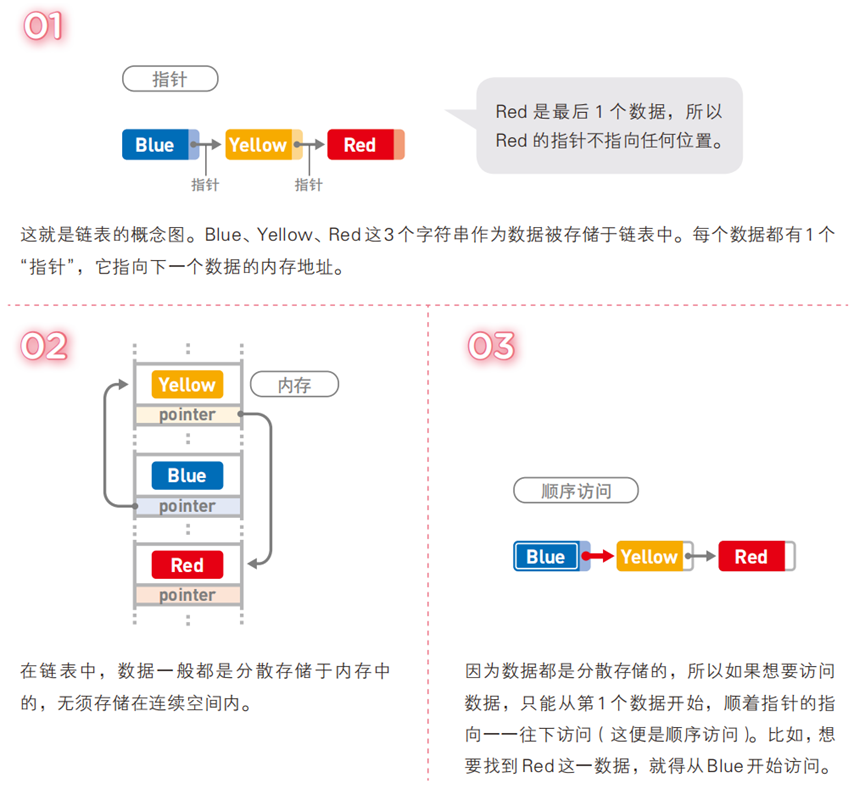
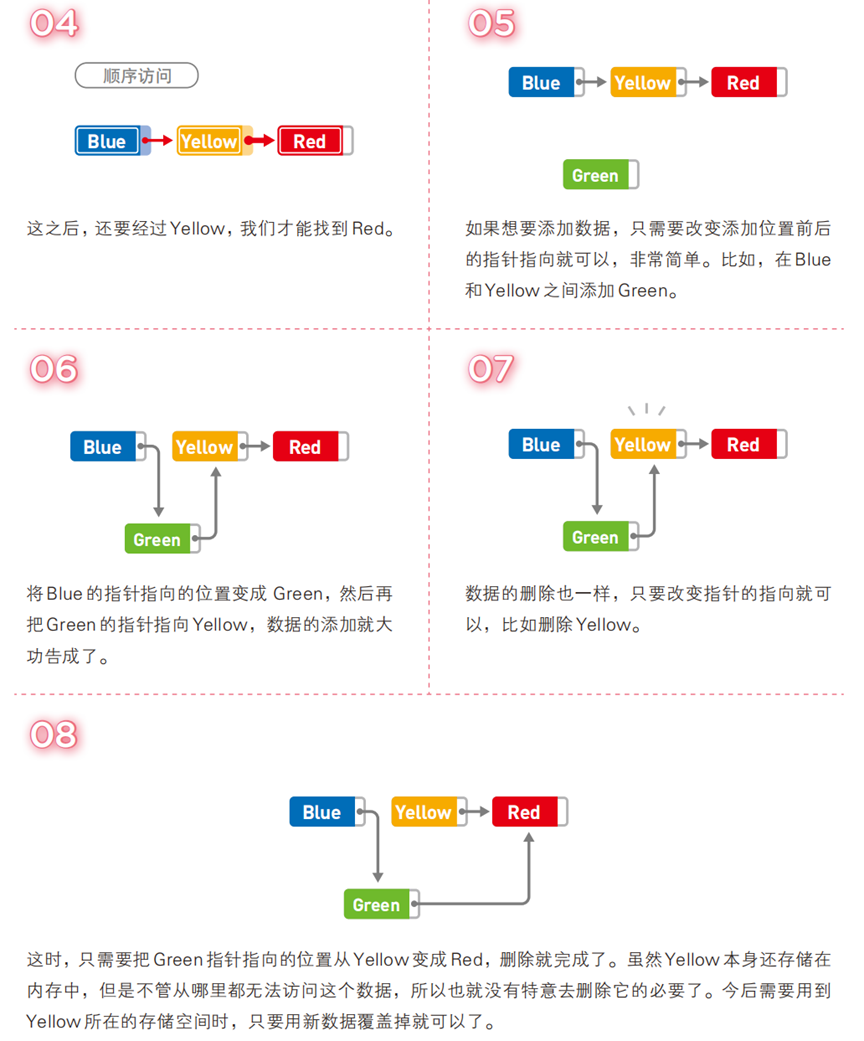
链表的分类

按节点结构和连接方式，链表可分为：

• 单链表：每个节点只有一个指针，指向后继节点
• 双链表：每个节点有两个指针，分别指向前驱和后继节点
• 循环链表：首尾相连的链表，可分为单循环链表和双循环链表

按是否包含头节点，可分为：

• 带头节点的链表
• 不带头节点的链表

链表与数组的对比

特性	链表	数组
内存存储	非连续	连续
随机访问	O(n)	O(1)
插入 / 删除	O (1)（已知位置）	O(n)
空间效率	较低（需存储指针）	较高
动态扩容	天然支持	需要重新分配内存
实现复杂度	较高	较低

单链表

单链表的结构

单链表的每个节点包含数据域和一个指向后继节点的指针：

typedef struct Node {
    int data;          // 数据域
    struct Node* next; // 指针域，指向后继节点
} Node;

单链表(带头节点)

带头节点的单链表在首节点前增加一个特殊节点（头节点），头节点不存储有效数据，仅用于简化操作。

基本操作

• 初始化链表

Node* create_node(int data) {
    // 为新节点分配内存（大小为 Node 结构体）
    Node* new_node = (Node*)malloc(sizeof(Node));
    if (new_node == NULL) {  // 检查内存分配是否成功
        printf("内存分配失败！\n");
        exit(1);  // 分配失败时退出程序（或根据需求处理错误）
    }
    
    // 初始化节点：设置数据，指针域暂为 NULL
    new_node->data = data;
    new_node->next = NULL;
    
    return new_node;  // 返回新节点的地址
}

Node* init_list() {
    Node* head_node = create_node(0); // 头节点数据无意义
    head_node->next = NULL;
    return head_node;
}

• 插入操作
  

  • 头部插入（在首节点前插入）

  // 不需要二级指针，因为头节点固定不变
  void insert_head(Node* head_node, int data) {
      Node* new_node = create_node(data);
      new_node->next = head_node->next;
      head_node->next = new_node;
  }
  

  • 尾部插入

  void insert_tail(Node* head_node, int data) {
      Node* new_node = create_node(data);
      
      // 找到尾节点
      Node* curr = head_node;
      while (curr->next != NULL) {
          curr = curr->next;
      }
      
      curr->next = new_node;
  }
  

  • 中间插入

  // 在值为target的节点后插入新节点
  void insert_middle(Node* head_node, int target, int data) {
      // 创建新节点
      Node* new_node = create_node(data);
      if (new_node == NULL) {
          printf("内存分配失败，插入失败\n");
          return;
      }
      
      // 遍历链表寻找目标节点
      Node* curr = head_node->next;  // 从第一个有效节点开始遍历
      while (curr != NULL) {
          if (curr->data == target) {
              // 找到目标节点，执行插入操作
              new_node->next = curr->next;  // 新节点指向目标节点的下一个节点
              curr->next = new_node;        // 目标节点指向新节点
              printf("已在值为%d的节点后插入数据%d\n", target, data);
              return;
          }
          curr = curr->next;  // 继续遍历下一个节点
      }
      
      // 若未找到目标节点
      printf("未找到值为%d的节点，插入失败\n", target);
      free(new_node);  // 释放未使用的新节点，避免内存泄漏
  }
  

• 查找操作（按值 / 按位置）

  • 按值查找（返回第一个匹配节点的指针）

  // 查找值为target的第一个有效节点，返回其指针；未找到返回NULL
  Node* find_by_value_singly(Node* head_node, int target) {
      Node* curr = head_node->next; // 从首节点开始遍历有效节点
      while (curr != NULL) {
          if (curr->data == target) {
              return curr; // 找到目标节点
          }
          curr = curr->next;
      }
      return NULL; // 未找到
  }
  

  • 应用：用于定位需要修改或删除的节点（避免重复遍历）。
  • 按位置查找（返回第 n 个有效节点的指针）

  // 查找第n个有效节点（首节点为第1个），返回其指针；越界/无效输入返回NULL
  Node* find_by_index_singly(Node* head_node, int n) {
      // 检查头节点是否为空（避免传入未初始化的链表）
      if (head_node == NULL) {
          printf("错误：头节点为空（链表未初始化）！\n");
          return NULL;
      }
  
      // 检查n是否为有效正数（n必须>0）
      if (n <= 0) {
          printf("错误：位置无效（n必须为正整数）！\n");
          return NULL;
      }
  
      // 从首节点（head_node->next）开始遍历
      Node* curr = head_node->next;
      int count = 1;  // 计数器：首节点为第1个
  
      // 遍历到第n个节点，或链表结束（curr为NULL）
      while (curr != NULL && count < n) {
          curr = curr->next;
          count++;
      }
  
      // 判断结果：若curr为NULL，说明n超过链表长度
      if (curr == NULL) {
          printf("错误：n=%d超过链表长度（链表有效节点数不足%d个）！\n", n, n);
      }
  
      return curr;  // 找到则返回节点指针，否则返回NULL
  } 
  

  • 注意：空链表或n超过链表长度时返回NULL，需在调用处判断。

• 修改操作（按值 / 按位置修改）

  • 按值修改（修改第一个匹配节点的数据）

  // 将第一个值为old_val的节点修改为new_val，成功返回1，失败返回0
  int update_by_value_singly(Node* head_node, int old_val, int new_val) {
      Node* target = find_by_value_singly(head_node, old_val);
      if (target == NULL) {
          printf("未找到值为%d的节点，修改失败！\n", old_val);
          return 0;
      }
      target->data = new_val;
      return 1;
  }
  

  • 按位置修改（修改第 n 个节点的数据）

  // 将第n个有效节点的数据修改为new_val，成功返回1，失败返回0
  int update_by_index_singly(Node* head_node, int n, int new_val) {
      Node* target = find_by_index_singly(head_node, n);
      if (target == NULL) {
          printf("第%d个节点不存在，修改失败！\n", n);
          return 0;
      }
      target->data = new_val;
      return 1;
  }
  

• 删除操作
  

  • 删除首节点

  void delete_head(Node* head_node) {
      if (head_node->next == NULL) {
          printf("链表为空，无法删除\n");
          return;
      }
      
      Node* temp = head_node->next;
      head_node->next = temp->next;
      free(temp);
  }
  

• 遍历链表

void traverse_singly(Node* head_node) {
    if (head_node->next == NULL) { // 空链表
        printf("单链表（带头节点）：空\n");
        return;
    }
    Node* curr = head_node->next;
    printf("单链表（带头节点）：");
    while (curr != NULL) {
        printf("%d → ", curr->data);
        curr = curr->next;
    }
    printf("NULL\n");
}

• 销毁链表

// 单链表（带头节点）销毁的正确实现（需要二级指针）
void destroy_singly_list(Node** head_node) {
    if (*head_node == NULL) return;
    
    Node* curr = *head_node;
    Node* temp;
    
    // 释放所有节点
    while (curr != NULL) {
        temp = curr;
        curr = curr->next;
        free(temp);
    }
    
    // 关键：将外部的头指针置为NULL，避免野指针
    *head_node = NULL; 
}

• 注:链表销毁操作必须使用二级指针，核心原因是 “需要修改外部一级指针变量本身的值”，而非 “释放头节点内存”

单链表(不带头节点)

基本操作

• 创建节点

Node* create_node(int data) {
    Node* new_node = (Node*)malloc(sizeof(Node));
    if (new_node == NULL) {
        printf("内存分配失败\n");
        exit(1);
    }
    new_node->data = data;
    new_node->next = NULL;
    return new_node;
}

• 初始化链表

Node* init_list() {
    return NULL; // 空链表头指针为NULL
}

• 插入操作

  • 头部插入

  // 注意：需要传递头指针的地址（二级指针），因为要修改头指针
  void insert_head(Node** head, int data) {
      Node* new_node = create_node(data);
      new_node->next = *head; // 新节点指向原头节点
      *head = new_node;       // 更新头指针
  }
  

  • 尾部插入

  /*尾部插入必须使用二级指针，原因与头部插入类似：
  当链表为空时（*head == NULL），需要修改头指针本身（让头指针指向新节点）*/
  void insert_tail(Node** head, int data) {
      Node* new_node = create_node(data);
      
      // 空链表特殊处理
      if (*head == NULL) {
          *head = new_node;
          return;
      }
      
      // 找到尾节点
      Node* curr = *head;
      while (curr->next != NULL) {
          curr = curr->next;
      }
      curr->next = new_node;
  }
  

  • 中间插入（在值为 target 的节点后插入）

  void insert_after(Node** head, int target, int data) {
      if (*head == NULL) {
          printf("链表为空，无法插入\n");
          return;
      }
      
      // 查找目标节点
      Node* curr = *head;
      while (curr != NULL && curr->data != target) {
          curr = curr->next;
      }
      
      if (curr == NULL) {
          printf("未找到目标节点\n");
          return;
      }
      
      // 插入新节点
      Node* new_node = create_node(data);
      new_node->next = curr->next;
      curr->next = new_node;
  }
  

• 查找操作

  • 按值查找（返回第一个匹配的节点指针）

  // head：头指针（直接指向首节点，空链表为NULL）
  // target：待查找的目标值
  // 返回值：匹配节点指针（NULL表示未找到或空链表）
  Node* find_by_value_no_head(Node* head, int target) {
      // 边界1：空链表，直接返回NULL
      if (head == NULL) {
          printf("链表为空，无法查找！\n");
          return NULL;
      }
  
      // 遍历所有有效节点（从首节点head开始）
      Node* curr = head;
      while (curr != NULL) {
          if (curr->data == target) {
              return curr; // 找到目标节点，返回指针
          }
          curr = curr->next; // 指针后移
      }
  
      // 边界2：遍历完所有节点，未找到目标
      printf("未找到值为%d的节点！\n", target);
      return NULL;
  }
  

  • 空链表直接返回NULL，避免后续遍历空指针；
  • 遍历终止条件为curr == NULL（不带头节点无 “头节点锚点”，以NULL标识链表结尾）。
  • 按位置查找（返回第 n 个有效节点的指针）

  // head：头指针（直接指向首节点）
  // n：目标位置（1-based，首节点为第1个）
  // 返回值：第n个节点指针（NULL表示位置无效或越界）
  Node* find_by_index_no_head(Node* head, int n) {
      // 边界1：位置无效（n必须为正整数）
      if (n <= 0) {
          printf("位置无效！必须输入大于0的整数（首节点为第1个）。\n");
          return NULL;
      }
  
      // 边界2：空链表，无法查找任何位置
      if (head == NULL) {
          printf("链表为空，无法查找第%d个节点！\n", n);
          return NULL;
      }
  
      // 遍历定位第n个节点（计数器从1开始，对应首节点）
      Node* curr = head;
      int curr_index = 1;
      while (curr != NULL && curr_index < n) {
          curr = curr->next;
          curr_index++;
      }
  
      // 边界3：n超过链表长度（curr已为NULL，未遍历到第n个节点）
      if (curr == NULL) {
          printf("链表长度不足！当前链表仅%d个节点，无法查找第%d个节点。\n", curr_index - 1, n);
          return NULL;
      }
  
      // 找到第n个节点，返回指针
      return curr;
  }
  

  • 先判断位置有效性（n<=0直接返回错误），再处理空链表；
  • 遍历终止条件为 “找到第n个节点” 或 “遍历到链表结尾（curr==NULL）”，后者表示n越界。

• 修改操作

  • 按值修改（修改第一个匹配节点的数据）

  // head：头指针（直接指向首节点）
  // old_val：待修改的旧值
  // new_val：修改后的新值
  // 返回值：1（成功），0（失败）
  int update_by_value_no_head(Node* head, int old_val, int new_val) {
      // 步骤1：先通过“按值查找”定位目标节点
      Node* target_node = find_by_value_no_head(head, old_val);
      
      // 步骤2：判断是否找到目标节点
      if (target_node == NULL) {
          return 0; // 未找到，修改失败
      }
  
      // 步骤3：修改目标节点的数据域
      target_node->data = new_val;
      printf("成功将值%d修改为%d！\n", old_val, new_val);
      return 1;
  }
  

  • 直接复用find_by_value_no_head函数，避免重复遍历代码；
  • 查找失败时返回0，调用者可通过返回值判断修改结果。
  • 按位置修改（修改第 n 个节点的数据）

  // head：头指针（直接指向首节点）
  // n：目标位置（1-based）
  // new_val：修改后的新值
  // 返回值：1（成功），0（失败）
  int update_by_index_no_head(Node* head, int n, int new_val) {
      // 步骤1：先通过“按位置查找”定位目标节点
      Node* target_node = find_by_index_no_head(head, n);
      
      // 步骤2：判断是否找到目标节点
      if (target_node == NULL) {
          return 0; // 位置无效/越界/空链表，修改失败
      }
  
      // 步骤3：修改目标节点的数据域
      target_node->data = new_val;
      printf("成功将第%d个节点的值修改为%d！\n", n, new_val);
      return 1;
  }
  

  • 复用find_by_index_no_head函数，自动处理位置无效、越界等边界；
  • 修改仅操作数据域，无需调整指针（与带头节点一致）。

• 删除节点

  • 删除首节点

  void delete_head(Node** head) {
      if (*head == NULL) {
          printf("链表为空，无法删除\n");
          return;
      }
      
      Node* temp = *head;
      *head = (*head)->next; // 更新头指针
      free(temp);
  }
  

  • 删除尾节点

  void delete_tail(Node** head) {
      if (*head == NULL) {
          printf("链表为空，无法删除\n");
          return;
      }
      
      // 只有一个节点的情况
      if ((*head)->next == NULL) {
          free(*head);
          *head = NULL;
          return;
      }
      
      // 找到倒数第二个节点
      Node* curr = *head;
      while (curr->next->next != NULL) {
          curr = curr->next;
      }
      
      free(curr->next);
      curr->next = NULL;
  }
  

  • 删除指定值的节点

  void delete_value(Node** head, int target) {
      if (*head == NULL) {
          printf("链表为空，无法删除\n");
          return;
      }
      
      // 若删除的是头节点
      if ((*head)->data == target) {
          Node* temp = *head;
          *head = (*head)->next;
          free(temp);
          return;
      }
      
      // 查找目标节点的前驱
      Node* curr = *head;
      while (curr->next != NULL && curr->next->data != target) {
          curr = curr->next;
      }
      
      if (curr->next == NULL) {
          printf("未找到目标节点\n");
          return;
      }
      
      // 删除节点
      Node* temp = curr->next;
      curr->next = temp->next;
      free(temp);
  }
  

• 遍历操作

void traverse(Node* head) {
    if (head == NULL) {
        printf("链表为空\n");
        return;
    }
    
    Node* curr = head;
    while (curr != NULL) {
        printf("%d -> ", curr->data);
        curr = curr->next;
    }
    printf("NULL\n");
}

• 销毁链表

  // 不带头节点的单链表销毁（必须用二级指针）
  void destroy_no_head(Node** head) {
      if (*head == NULL) {
          printf("链表为空，无需销毁\n");
          return;
      }
      
      Node* curr = *head;
      Node* temp;
      
      // 释放所有数据节点
      while (curr != NULL) {
          temp = curr;
          curr = curr->next;
          free(temp);
      }
      
      // 关键：将外部头指针置为NULL（必须通过二级指针）
      *head = NULL;
      printf("不带头节点的链表已销毁\n");
  }
  

进阶操作

• 链表反转

Node* reverse(Node* head) {
    Node *prev = NULL, *curr = head, *next = NULL;
    
    while (curr != NULL) {
        next = curr->next; // 保存后继节点
        curr->next = prev; // 反转指针
        prev = curr;       // 移动前驱指针
        curr = next;       // 移动当前指针
    }
    
    return prev; // prev成为新的头指针
}

• 求链表长度

int length(Node* head) {
    int len = 0;
    Node* curr = head;
    while (curr != NULL) {
        len++;
        curr = curr->next;
    }
    return len;
}

• 查找中间节点

Node* find_middle(Node* head) {
    if (head == NULL) return NULL;
    
    Node *slow = head, *fast = head;
    while (fast != NULL && fast->next != NULL) {
        slow = slow->next;      // 慢指针走一步
        fast = fast->next->next; // 快指针走两步
    }
    
    return slow;
}

带头节点与不带头节点的对比

操作	不带头节点	带头节点
初始化	头指针为 NULL	创建头节点，头指针指向头节点
头部插入	需要修改头指针（二级指针）	无需修改头指针
空链表判断	头指针 == NULL	头节点 ->next == NULL
边界处理	复杂（需特殊处理空链表）	简单（统一操作逻辑）
内存开销	较小	较大（多一个节点）

双链表

双链表每个节点有两个指针，分别指向前驱节点和后继节点，支持双向遍历。

双链表的结构

typedef struct DNode {
    int data;           // 数据域
    struct DNode* prev; // 指向前驱节点
    struct DNode* next; // 指向后继节点
} DNode;

双链表(带头节点)

• 基本操作

  • 创建节点

  DNode* create_dnode(int data) {
      DNode* new_node = (DNode*)malloc(sizeof(DNode));
      if (new_node == NULL) {
          printf("内存分配失败\n");
          exit(1);
      }
      new_node->data = data;
      new_node->prev = NULL;
      new_node->next = NULL;
      return new_node;
  }
  

  • 初始化链表

  DNode* init_dlist() {
      DNode* head_node = create_dnode(0); // 头节点
      head_node->prev = NULL;
      head_node->next = NULL;
      return head_node;
  }
  

  • 插入操作

    • 头部插入

    void insert_head(DNode* head_node, int data) {
        DNode* new_node = create_dnode(data);
        DNode* first_node = head_node->next;
        
        new_node->next = first_node;
        new_node->prev = head_node;
        
        head_node->next = new_node;
        if (first_node != NULL) {
            first_node->prev = new_node;
        }
    }
    

    • 尾部插入

    void insert_tail(DNode* head_node, int data) {
        DNode* new_node = create_dnode(data);
        
        // 找到尾节点
        DNode* curr = head_node;
        while (curr->next != NULL) {
            curr = curr->next;
        }
        
        curr->next = new_node;
        new_node->prev = curr;
    }
    

  • 按值查找

  // 按值查找，双向遍历（从首节点和尾节点同时查找，优化长链表效率）
  DNode* find_by_value_doubly(DNode* head_node, int target) {
      if (head_node->next == NULL) return NULL; // 空链表
      
      DNode* front = head_node->next; // 首节点开始
      DNode* rear = head_node->next;  // 先定位尾节点
      while (rear->next != NULL) {
          rear = rear->next;
      }
      
      // 双向遍历，相遇则终止
      while (front != rear && front->prev != rear) {
          if (front->data == target) return front;
          if (rear->data == target) return rear;
          front = front->next;
          rear = rear->prev;
      }
      // 检查相遇节点
      if (front->data == target) return front;
      return NULL;
  }
  

  • 按位置修改

  // 修改第n个有效节点的数据
  int update_by_index_doubly(DNode* head_node, int n, int new_val) {
      if (n <= 0) return 0;
      DNode* curr = head_node->next;
      int count = 1;
      while (curr != NULL && count < n) {
          curr = curr->next;
          count++;
      }
      if (curr == NULL) return 0; // 越界
      curr->data = new_val;
      return 1;
  }
  

  • 删除操作(删除指定值的节点)

  void delete_value(DNode* head_node, int target) {
      DNode* curr = head_node->next;
      
      while (curr != NULL && curr->data != target) {
          curr = curr->next;
      }
      
      if (curr == NULL) {
          printf("未找到目标节点\n");
          return;
      }
      
      // 调整前驱和后继的指针
      DNode* prev_node = curr->prev;
      DNode* next_node = curr->next;
      
      prev_node->next = next_node;
      if (next_node != NULL) {
          next_node->prev = prev_node;
      }
      
      free(curr);
  }
  

  • 遍历操作(正向遍历)

  void traverse_forward(DNode* head_node) {
      DNode* curr = head_node->next;
      if (curr == NULL) {
          printf("链表为空\n");
          return;
      }
      
      while (curr != NULL) {
          printf("%d <-> ", curr->data);
          curr = curr->next;
      }
      printf("NULL\n");
  }
  

  • 反向遍历

  void traverse_backward(DNode* head_node) {
      DNode* curr = head_node;
      
      // 找到尾节点
      while (curr->next != NULL) {
          curr = curr->next;
      }
      
      if (curr == head_node) { // 空链表
          printf("链表为空\n");
          return;
      }
      
      while (curr != head_node) {
          printf("%d <-> ", curr->data);
          curr = curr->prev;
      }
      printf("头节点\n");
  }
  

• 销毁链表

  void destroy_double_cycle(DNode** head_node) {
      if (*head_node == NULL) {
          printf("链表已空，无需销毁\n");
          return;
      }
      
      DNode* curr = (*head_node)->next;  // 从第一个数据节点开始
      DNode* temp;
      
      // 遍历释放所有数据节点（终止条件：回到头节点）
      while (curr != *head_node) {
          temp = curr;          // 保存当前节点
          curr = curr->next;    // 移动到下一个节点（释放前先获取下一个地址）
          free(temp);           // 释放当前节点
      }
      
      // 释放头节点
      free(*head_node);
      // 关键：通过二级指针将外部头指针置为NULL，避免野指针
      *head_node = NULL;
      
      printf("双循环链表已完全销毁\n");
  }
  

双链表的优势与应用场景

• 优势：
  • 支持双向遍历，方便查找前驱节点
  • 删除操作更高效，无需从头遍历查找前驱
  • 适合需要频繁在两端操作的场景
• 应用场景：
  • 实现双向队列
  • 浏览器的前进 / 后退功能
  • 文本编辑器的光标移动

循环链表

循环链表的尾节点不指向 NULL，而是指向头节点（或头指针指向的节点），形成一个闭环。

单循环链表

单循环链表是单链表的变形，尾节点的 next 指针指向头节点（或首节点）。

• 单循环链表(带头节点)

  • 初始化

  Node* init_cycle_list() {
      Node* head_node = create_node(0); // 头节点
      head_node->next = head_node; // 空循环链表，头节点指向自己
      return head_node;
  }
  

  • 插入操作（尾部插入）

  void insert_tail(Node* head_node, int data) {
      Node* new_node = create_node(data);
      Node* curr = head_node;
      
      // 找到尾节点（尾节点的next是头节点）
      while (curr->next != head_node) {
          curr = curr->next;
      }
      
      curr->next = new_node;
      new_node->next = head_node; // 新节点指向头节点，维持循环
  }
  

  • 按值查找

  // 单循环链表（带头节点）中查找值为target的节点
  Node* find_in_cycle_singly(Node* head_node, int target) {
      // 空循环链表：头节点next指向自身
      if (head_node->next == head_node) return NULL;
      
      Node* curr = head_node->next; // 从首节点开始
      // 遍历终止条件：回到头节点
      while (curr != head_node) {
          if (curr->data == target) {
              return curr;
          }
          curr = curr->next;
      }
      return NULL;
  }
  

  • 修改操作（按值修改）

  // 将第一个值为old_val的节点修改为new_val
  void modify_cycle_list(Node* head_node, int old_val, int new_val) {
      if (head_node->next == head_node) {
          printf("循环链表为空，无法修改\n");
          return;
      }
      
      Node* curr = head_node->next;
      while (curr != head_node) {
          if (curr->data == old_val) {
              curr->data = new_val;
              printf("已将值%d修改为%d\n", old_val, new_val);
              return;
          }
          curr = curr->next;
      }
      
      printf("未找到值为%d的节点，修改失败\n", old_val);
  }
  

  • 删除操作（按值删除）

  // 删除第一个值为target的节点
  void delete_node(Node* head_node, int target) {
      if (head_node->next == head_node) {
          printf("循环链表为空，无法删除\n");
          return;
      }
      
      Node* prev = head_node;    // 前驱节点
      Node* curr = head_node->next;  // 当前节点
      
      while (curr != head_node) {
          if (curr->data == target) {
              prev->next = curr->next;  // 前驱节点指向当前节点的下一个
              free(curr);  // 释放当前节点内存
              printf("已删除值为%d的节点\n", target);
              return;
          }
          prev = curr;
          curr = curr->next;
      }
      
      printf("未找到值为%d的节点，删除失败\n", target);
  }
  

  • 遍历操作

  void traverse(Node* head_node) {
      if (head_node->next == head_node) {
          printf("循环链表为空\n");
          return;
      }
      
      Node* curr = head_node->next;
      while (curr != head_node) {
          printf("%d -> ", curr->data);
          curr = curr->next;
      }
      printf("(回到头节点)\n");
  }
  

  • 销毁链表

  // 销毁整个单循环链表（包括头节点）
  void destroy_cycle_list(Node** head_node) {
      if (*head_node == NULL) return;  // 链表已空
      
      Node* curr = (*head_node)->next;
      Node* temp;
      
      // 先释放所有数据节点
      while (curr != *head_node) {
          temp = curr;
          curr = curr->next;
          free(temp);
      }
      
      // 最后释放头节点
      free(*head_node);
      *head_node = NULL;  // 避免野指针
      printf("单循环链表已销毁\n");
  }
  

双循环链表

双循环链表是双链表的变形，尾节点的 next 指向头节点，头节点的 prev 指向尾节点。

• 初始化

DNode* init_double_cycle_list() {
    DNode* head_node = create_dnode(0); // 头节点
    head_node->prev = head_node; // 头节点的prev指向自己
    head_node->next = head_node; // 头节点的next指向自己
    return head_node;
}

• 插入操作（尾部插入）

void insert_tail(DNode* head_node, int data) {
    DNode* new_node = create_dnode(data);
    DNode* last_node = head_node->prev; // 尾节点是头节点的前驱
    
    // 插入新节点
    last_node->next = new_node;
    new_node->prev = last_node;
    new_node->next = head_node;
    head_node->prev = new_node;
}

• 修改操作（按值修改）

// 将第一个值为old_val的节点修改为new_val
void modify_double_cycle(DNode* head_node, int old_val, int new_val) {
    if (head_node->next == head_node) {
        printf("双循环链表为空，无法修改\n");
        return;
    }
    
    DNode* curr = head_node->next;
    while (curr != head_node) {
        if (curr->data == old_val) {
            curr->data = new_val;
            printf("已将值%d修改为%d\n", old_val, new_val);
            return;
        }
        curr = curr->next;
    }
    
    printf("未找到值为%d的节点，修改失败\n", old_val);
}

• 删除操作（按值删除）

// 删除第一个值为target的节点
void delete_dnode(DNode* head_node, int target) {
    if (head_node->next == head_node) {
        printf("双循环链表为空，无法删除\n");
        return;
    }
    
    DNode* curr = head_node->next;
    while (curr != head_node) {
        if (curr->data == target) {
            // 调整前驱节点的next指针
            curr->prev->next = curr->next;
            // 调整后继节点的prev指针
            curr->next->prev = curr->prev;
            free(curr);  // 释放当前节点
            printf("已删除值为%d的节点\n", target);
            return;
        }
        curr = curr->next;
    }
    
    printf("未找到值为%d的节点，删除失败\n", target);
}

• 销毁链表

// 销毁整个双循环链表（包括头节点）
void destroy_double_cycle(DNode** head_node) {
    if (*head_node == NULL) return;  // 链表已空
    
    DNode* curr = (*head_node)->next;
    DNode* temp;
    
    // 先释放所有数据节点
    while (curr != *head_node) {
        temp = curr;
        curr = curr->next;
        free(temp);
    }
    
    // 最后释放头节点
    free(*head_node);
    *head_node = NULL;  // 避免野指针
    printf("双循环链表已销毁\n");
}

循环链表的应用场景

• 约瑟夫环问题
• 循环队列实现
• 资源调度算法
• 音乐播放器的循环播放列表

链表的经典问题

• 判断链表是否有环

#include <stdbool.h>
/*如果链表中存在环，快指针最终会追上慢指针（两者指向同一个节点）；
如果链表中没有环，快指针会先到达链表末尾（指向 NULL）
*/
bool has_cycle(Node* head) {
    if (head == NULL || head->next == NULL) {
        return false;
    }
    
    Node *slow = head, *fast = head->next;
    while (slow != fast) {
        if (fast == NULL || fast->next == NULL) {
            return false;
        }
        slow = slow->next;
        fast = fast->next->next;
    }
    return true;
}

• 找到环的入口节点

Node* find_cycle_entry(Node* head) {
    if (head == NULL || head->next == NULL) {
        return NULL;
    }
    
    // 第一步：判断是否有环，获取相遇点
    Node *slow = head, *fast = head;
    bool has_cycle = false;
    
    while (fast != NULL && fast->next != NULL) {
        slow = slow->next;
        fast = fast->next->next; 
        if (slow == fast) {
            has_cycle = true;
            break;
        }
    }
    
    if (!has_cycle) {
        return NULL;
    }
    /*两指针相遇时，慢指针走了L步，快指针走了2L步,接下来同步走L-当前位置到入口的距离
	快指针从当前位置走，慢指针从头走，二者相遇即为入口*/
    // 第二步：找到环入口
    slow = head;
    while (slow != fast) {
        slow = slow->next;
        fast = fast->next;
    }
    
    return slow;
}

• 合并两个有序链表

Node* merge_two_lists(Node* l1, Node* l2) {
    // 创建哑节点作为临时头节点
    Node dummy;
    Node* curr = &dummy;
    
    while (l1 != NULL && l2 != NULL) {
        if (l1->data <= l2->data) {
            curr->next = l1;
            l1 = l1->next;
        } else {
            curr->next = l2;
            l2 = l2->next;
        }
        curr = curr->next;
    }
    
    // 处理剩余节点
    curr->next = (l1 != NULL) ? l1 : l2;
    
    return dummy.next;
}

• 删除链表的倒数第 k 个节点

Node* remove_nth_from_end(Node* head, int k) {
    // 创建哑节点简化边界处理
    Node dummy;
    dummy.next = head;
    Node *fast = &dummy, *slow = &dummy;
    
    // 快指针先移动k步
    for (int i = 0; i < k; i++) {
        if (fast->next == NULL) {
            return head; // k大于链表长度，不删除
        }
        fast = fast->next;
    }
    
    // 快慢指针同时移动，直到快指针到达尾部
    while (fast->next != NULL) {
        fast = fast->next;
        slow = slow->next;
    }
    
    // 删除倒数第k个节点
    Node* temp = slow->next;
    slow->next = temp->next;
    free(temp);
    
    return dummy.next;
}

链表的实现注意事项

• 内存管理
  • 动态分配节点后要检查是否分配成功
  • 删除节点后要及时释放内存，避免内存泄漏
  • 销毁链表时要遍历所有节点并释放
• 指针操作
  • 操作指针前要确保指针不为 NULL，避免空指针异常
  • 修改指针指向时要先保存必要的指针，避免指针丢失
  • 双链表操作要同时维护 prev 和 next 指针，确保一致性
• 边界条件处理
  • 空链表的处理
  • 单节点链表的处理
  • 头节点和尾节点的特殊处理
  • 循环链表的终止条件处理
• 选择合适的链表类型
  • 只需单向遍历且内存受限：单链表
  • 需要双向遍历或频繁在两端操作：双链表
  • 需要循环访问或实现环形结构：循环链表
  • 操作频繁且希望简化代码：带头节点的链表