RSA 数论技巧

写在前言：持续更新中...

光滑数

定义

对于一个数 \(n\)，如果它能够被唯一分解为 \(n = p_{1}^{\alpha_1}p_{2}^{\alpha_2} \dots p_{s}^{\alpha_s}(p_1 < p_2 < ... < p_s)\)，如果对于所有的 \(p_i(1 \le i \le s)\) 均有 \(p_i \le B\)，那么我们称这个数为 \(B - \text{光滑}\) 的。

很多算法是基于 \(B\) 较小的情况来进行解决，我们可以看下面的例题来学习，以下 \(B - \text{光滑}\) 的数若 \(B\) 较小，简称光滑数。

p - 1 光滑

Pollard's 算法

若 \(p\) 是 \(n\) 的因数，并且 \(p − 1\) 是光滑数，可以考虑使用 Pollard's 算法来分解 \(n\)。

Wiki 上的算法流程如下：

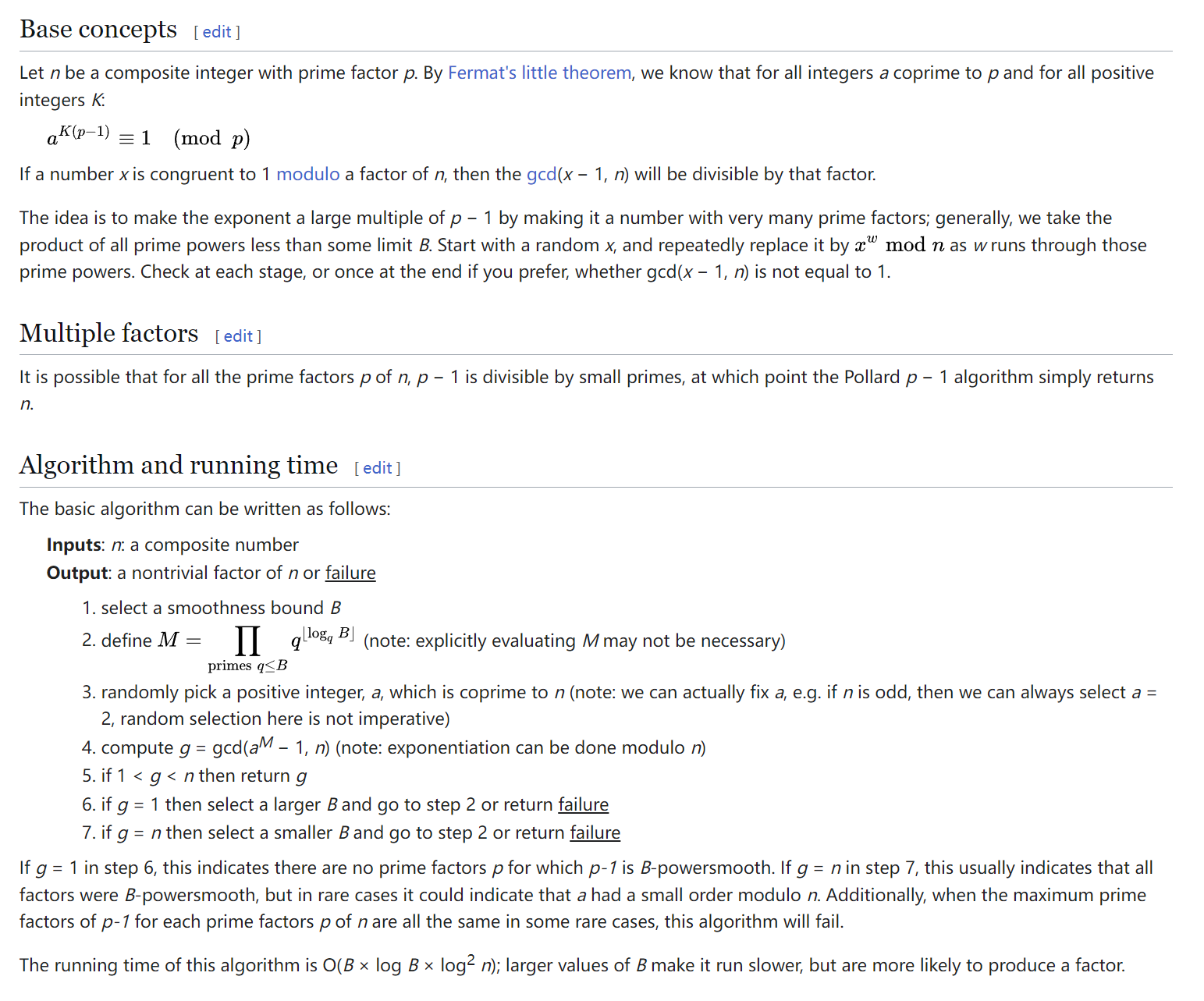
由于 \(p - 1\) 是光滑的，选取一个 \(B\) 使得 \((p - 1) \mid B!\)。

根据费马小定理，我们有：

\[a^{p-1} \equiv 1 (\bmod ~ p) \]

那么可以推出 \(a^{K(p-1)} \equiv 1 \pmod p\)。

由于 \(B! = K(p-1)\)，所以 \(a^{B!} \equiv 1 \pmod p\)

因此 \(a^{B!} - 1 = k_{1}p\)。

同时，让 \(a^{B!}\) 模 \(n\) 有 \(a^{B!} \equiv A \pmod n\)

因此 \(a^{B!} - A = k_{2}n\)。

上述两式相减可得 \(A - 1 = k_{2}n - k_{1}p\)。

不难发现 \(p = \gcd{(A - 1, ~ n)}\)。

注意：选取恰当的 \(B\) 是必要的，如果 \(n = pq\) 中 \(p, ~ q\) 两个因子均是光滑的，且 \((p - 1) \mid B!\) 与 \((q - 1) \mid B!\) 同时成立，那么此时 \(a^{(p - 1)(q - 1)} \equiv 1 \pmod {pq}\) 此时计算 \(\gcd{(A - 1, ~ n)}\) 得到的结果为 \(n\)，同理，\(B\) 较小会导致 \(\gcd{(A - 1, ~ n)} = 1\)。

由于计算阶乘的算法效率低下，所以对于非光滑数这个算法没有意义。

下面我们来看一个例题。

SHCTF 2024 魔鬼的步伐

from Crypto.Util.number import *
from random import choice
from enc import flag

m = bytes_to_long(flag)
def get_primes(limit):
    primes = []
    is_prime = [True] * (limit + 1)
    for num in range(2, limit + 1):
        if is_prime[num]:
            primes.append(num)
            for multiple in range(num * num, limit + 1, num):
                is_prime[multiple] = False
    return primes

def get_Prime(bits):
    while True:
        n = 2
        while n.bit_length() < bits:
            n *= choice(primes)
        if isPrime(n + 1):
            return n + 1

e = 65537
primes = get_primes(e)
p = get_Prime(512)
q = get_Prime(512)
n = p*q
c = pow(m,e,n)
print(f"n = {n}")
print(f"e = {e}")
print(f"c = {c}")
'''
n = 391005776046755596699618659246340733279513517050143630792209612493300221058346162409182143062864675702996104615097739220521431717966140002923091879824285706802681307073746160973177190517416980825268203022023401016332004335037582180267013391314432153625679364386326204808730143431891425324668120649464691460108081
e = 65537
c = 143234875923924414196836790485715958182553144290862550786433431528452602241496206240152356816911891891888596692519884126258641274109685025389569676536718006741800941833337629087306702531952775237637889020188884538158307245138965948781078007989600030230701865185135035643226997549934727114764825219500382771617775
'''

通过代码可以发现 \(p, q\) 一定是 \(e - \text{光滑}\) 的，尝试将 \(B\) 取 \(e\) 进行运算发现结果为 \(n\)，因此我们在 \((1, ~ e)\) 中进行二分求得一个恰当的 \(B\)，时间复杂度是 \(O(e\log{e})\) 的，所以我们可以很快求出答案。

脚本如下：

from Crypto.Util.number import *
from gmpy2 import *
from math import factorial
n = 391005776046755596699618659246340733279513517050143630792209612493300221058346162409182143062864675702996104615097739220521431717966140002923091879824285706802681307073746160973177190517416980825268203022023401016332004335037582180267013391314432153625679364386326204808730143431891425324668120649464691460108081
e = 65537
c = 143234875923924414196836790485715958182553144290862550786433431528452602241496206240152356816911891891888596692519884126258641274109685025389569676536718006741800941833337629087306702531952775237637889020188884538158307245138965948781078007989600030230701865185135035643226997549934727114764825219500382771617775

l = 1
r = e
while (l < r):
    mid = l + r >> 1
    a = pow(2, math.factorial(mid), n)
    p = gmpy2.gcd(a - 1, n)
    if p == 1:
        l = mid + 1
        continue
    if p == n:
        r = mid - 1
        continue
    q = n // p
    d = gmpy2.invert(e, (p - 1) * (q - 1))
    m = pow(c, d, n)
    print(long_to_bytes(m))
    break