NewStar CTF 2024 Crypto
Week1
xor
#As a freshman starting in 2024, you should know something about XOR, so this task is for you to sign in.
from pwn import xor
#The Python pwntools library has a convenient xor() function that can XOR together data of different types and lengths
from Crypto.Util.number import bytes_to_long
key = b'New_Star_CTF'
flag='flag{*******************}'
m1 = bytes_to_long(bytes(flag[:13], encoding='utf-8'))
m2 = flag[13:]
c1 = m1 ^ bytes_to_long(key)
c2 = xor(key, m2)
print('c1=',c1)
print('c2=',c2)
'''
c1= 8091799978721254458294926060841
c2= b';:\x1c1<\x03>*\x10\x11u;'
'''
根据异或的性质 \(x ~ \oplus ~ y ~ = ~ z\) 则 \(x ~ \oplus ~ z ~ = ~ y\),我们通过逆运算可以得到答案,拼接起来就是flag。
脚本如下
from Crypto.Util.number import *
from pwn import xor
key = b'New_Star_CTF'
c1= 8091799978721254458294926060841
c2= b';:\x1c1<\x03>*\x10\x11u;'
m1 = c1 ^ bytes_to_long(key)
m2 = xor(c2, key)
print(long_to_bytes(m1) + m2)
Base
4C4A575851324332474E324547554B494A5A4446513653434E564D444154545A4B354D45454D434E4959345536544B474D5134513D3D3D3D
经过 base16 解码可以得到:
LJWXQ2C2GN2EGUKIJZDFQ6SCNVMDATTZK5MEEMCNIY4U6TKGMQ4Q====
经过 base32 解码可以得到:
ZmxhZ3tCQHNFXzBmX0NyWXB0MF9OMFd9
经过 base64 解码可以得到:
flag{B@sE_0f_CrYpt0_N0W}
一眼秒了
from Crypto.Util.number import *
from gmpy2 import *
from serct import flag
p = getPrime(512)
q = getPrime(512)
n = p*q
m = bytes_to_long(flag)
e = 65537
c = powmod(m, e, n)
print(n)
print(c)
# 52147017298260357180329101776864095134806848020663558064141648200366079331962132411967917697877875277103045755972006084078559453777291403087575061382674872573336431876500128247133861957730154418461680506403680189755399752882558438393107151815794295272358955300914752523377417192504702798450787430403387076153
# 48757373363225981717076130816529380470563968650367175499612268073517990636849798038662283440350470812898424299904371831068541394247432423751879457624606194334196130444478878533092854342610288522236409554286954091860638388043037601371807379269588474814290382239910358697485110591812060488786552463208464541069
把 \(n\) 丢进 factordb.com 自动出分解,按照 RSA 思路解决即可。
from Crypto.Util.number import *
from gmpy2 import *
n = 52147017298260357180329101776864095134806848020663558064141648200366079331962132411967917697877875277103045755972006084078559453777291403087575061382674872573336431876500128247133861957730154418461680506403680189755399752882558438393107151815794295272358955300914752523377417192504702798450787430403387076153
c = 48757373363225981717076130816529380470563968650367175499612268073517990636849798038662283440350470812898424299904371831068541394247432423751879457624606194334196130444478878533092854342610288522236409554286954091860638388043037601371807379269588474814290382239910358697485110591812060488786552463208464541069
p = 7221289171488727827673517139597844534869368289455419695964957239047692699919030405800116133805855968123601433247022090070114331842771417566928809956044421
q = 7221289171488727827673517139597844534869368289455419695964957239047692699919030405800116133805855968123601433247022090070114331842771417566928809956045093
e = 65537
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))
Strange King
密文 ksjr{EcxvpdErSvcDgdgEzxqjql}。
已知 flag 格式为 flag{?????????????????},我们猜测这是移位密码,对 ksjr 与 flag 做差可以发现差值分别为 \(5, ~ 7, ~ 9, ~ 11\),因此每一位 \(key\) 的公差为 \(2\),按照此思路对两个不同循环 A~Z 和 a~z 进行移位即可。
脚本如下
from Crypto.Util.number import *
# flag
c = b'ksjr{EcxvpdErSvcDgdgEzxqjql}'
m = b'flag'
for i in range(len(m)):
a = c[i]
b = m[i]
print(a - b)
key = 5
ans = b''
for i in range(len(c)):
s = c[i]
if s != bytes_to_long(b'{') and s != bytes_to_long(b'}'):
if s >= bytes_to_long(b'a') and bytes_to_long(b'z'):
s -= bytes_to_long(b'a')
b = (s - key + 26) % 26
b += bytes_to_long(b'a')
b = long_to_bytes(b)
ans += b
else:
s -= bytes_to_long(b'A')
b = (s - key + 26) % 26
b += bytes_to_long(b'A')
b = long_to_bytes(b)
ans += b
else:
ans += long_to_bytes(s)
key += 2
print(ans)
Week2
这是几次方? 疑惑!
from Crypto.Util.number import *
flag = b'flag{*****}'
p = getPrime(512)
q = getPrime(512)
n = p*q
e = 65537
m = bytes_to_long(flag)
c = pow(m, e, n)
hint = p^e + 10086
print("c =", c)
print("[n, e] =", [n, e])
print("hint =", hint)
'''
c = 36513006092776816463005807690891878445084897511693065366878424579653926750135820835708001956534802873403195178517427725389634058598049226914694122804888321427912070308432512908833529417531492965615348806470164107231108504308584954154513331333004804817854315094324454847081460199485733298227480134551273155762
[n, e] = [124455847177872829086850368685666872009698526875425204001499218854100257535484730033567552600005229013042351828575037023159889870271253559515001300645102569745482135768148755333759957370341658601268473878114399708702841974488367343570414404038862892863275173656133199924484523427712604601606674219929087411261, 65537]
hint = 12578819356802034679792891975754306960297043516674290901441811200649679289740456805726985390445432800908006773857670255951581884098015799603908242531673390
'''
^ 表示异或,加法的优先级高于异或,所以按照这个思路解决 \(p, ~ q\),就可以按照一般RSA思路解决了。
from Crypto.Util.number import *
from gmpy2 import *
e = 65537
c = 36513006092776816463005807690891878445084897511693065366878424579653926750135820835708001956534802873403195178517427725389634058598049226914694122804888321427912070308432512908833529417531492965615348806470164107231108504308584954154513331333004804817854315094324454847081460199485733298227480134551273155762
n = 124455847177872829086850368685666872009698526875425204001499218854100257535484730033567552600005229013042351828575037023159889870271253559515001300645102569745482135768148755333759957370341658601268473878114399708702841974488367343570414404038862892863275173656133199924484523427712604601606674219929087411261
hint = 12578819356802034679792891975754306960297043516674290901441811200649679289740456805726985390445432800908006773857670255951581884098015799603908242531673390
p = hint ^ e + 10086
q = n // p
d = gmpy2.invert(e, (p - 1) * (q - 1))
print(long_to_bytes(pow(c, d, n)))
Since you konw something
from pwn import xor
#The Python pwntools library has a convenient xor() function that can XOR together data of different types and lengths
from Crypto.Util.number import bytes_to_long
key = ?? #extremely short
FLAG = 'flag{????????}'
c = bytes_to_long(xor(FLAG,key))
print("c={}".format(c))
'''
c=218950457292639210021937048771508243745941011391746420225459726647571
'''
由于 \(key\) 很小,所以我们可以爆破。
from pwn import xor
from Crypto.Util.number import *
c = 218950457292639210021937048771508243745941011391746420225459726647571
m = long_to_bytes(c)
print(m)
for key in range(0xffffff):
flag = xor(m, long_to_bytes(key))
if (b'flag' in flag):
print(flag)
茶里茶气
from Crypto.Util.number import *
flag = "flag{*****}"
assert len( flag ) == 25
a = ""
for i in flag:
a += hex(ord(i))[2:]
l = int(a,16).bit_length()
print("l =" , l )
v0 = int(a,16)>>(l//2)
v1 = int(a,16)-(v0<<(l//2))
p = getPrime(l//2+10)
v2 = 0
derta = 462861781278454071588539315363
v3 = 489552116384728571199414424951
v4 = 469728069391226765421086670817
v5 = 564098252372959621721124077407
v6 = 335640247620454039831329381071
assert v1 < p and v0 < p and derta < p and v3 < p and v4 < p and v5 < p and v6 < p
for i in range(32):
v1 += (v0+v2) ^ ( 8*v0 + v3 ) ^ ( (v0>>7) + v4 ) ; v1 %= p
v0 += (v1+v2) ^ ( 8*v1 + v5 ) ^ ( (v1>>7) + v6 ) ; v0 %= p
v2 += derta ; v2 %= p
print( "p =" , p )
print( "v0 =" , v0 )
print( "v1 =" , v1 )
"""
l = 199
p = 446302455051275584229157195942211
v0 = 190997821330413928409069858571234
v1 = 137340509740671759939138452113480
"""
考虑异或的对称性,且在模 \(p\) 意义下我们没有任何信息丢失,我们只需要将原来的 for 循环逆向进行,就可以得到我们的答案。
from Crypto.Util.number import *
derta = 462861781278454071588539315363
v3 = 489552116384728571199414424951
v4 = 469728069391226765421086670817
v5 = 564098252372959621721124077407
v6 = 335640247620454039831329381071
l = 199
p = 446302455051275584229157195942211
v0 = 190997821330413928409069858571234
v1 = 137340509740671759939138452113480
v2 = derta * 32 % p
for _ in range(32):
v2 -= derta ; v2 %= p
v0 -= (v1 + v2) ^ ((v1 << 3) + v5) ^ ((v1 >> 7) + v6) ; v0 %= p
v1 -= (v0 + v2) ^ ((v0 << 3) + v3) ^ ((v0 >> 7) + v4) ; v1 %= p
a = (v0 << (l // 2)) + v1
flag = long_to_bytes(a)
print(flag)
Just one and more
from Crypto.Util.number import *
flag = b'flag{?????}'
m1 = bytes_to_long(flag[:len(flag)//2])
m2 = bytes_to_long(flag[len(flag)//2:])
e = 65537
p, q, r= (getPrime(512) for _ in range(3))
N=p*q*r
c1 = pow(m1, e, p)
c2 = pow(m2, e, N)
print(f'p={p}\nq={q}\nr={r}\nc1={c1}\nc2={c2}')
'''
p=11867061353246233251584761575576071264056514705066766922825303434965272105673287382545586304271607224747442087588050625742380204503331976589883604074235133
q=11873178589368883675890917699819207736397010385081364225879431054112944129299850257938753554259645705535337054802699202512825107090843889676443867510412393
r=12897499208983423232868869100223973634537663127759671894357936868650239679942565058234189535395732577137079689110541612150759420022709417457551292448732371
c1=8705739659634329013157482960027934795454950884941966136315983526808527784650002967954059125075894300750418062742140200130188545338806355927273170470295451
c2=1004454248332792626131205259568148422136121342421144637194771487691844257449866491626726822289975189661332527496380578001514976911349965774838476334431923162269315555654716024616432373992288127966016197043606785386738961886826177232627159894038652924267065612922880048963182518107479487219900530746076603182269336917003411508524223257315597473638623530380492690984112891827897831400759409394315311767776323920195436460284244090970865474530727893555217020636612445
'''
非常标志的 RSA 题目,如果有困惑需要去复习 RSA 原理,模数的质数有多少个本质是没有区别的。
from Crypto.Util.number import *
from gmpy2 import *
e = 65537
p=11867061353246233251584761575576071264056514705066766922825303434965272105673287382545586304271607224747442087588050625742380204503331976589883604074235133
q=11873178589368883675890917699819207736397010385081364225879431054112944129299850257938753554259645705535337054802699202512825107090843889676443867510412393
r=12897499208983423232868869100223973634537663127759671894357936868650239679942565058234189535395732577137079689110541612150759420022709417457551292448732371
c1=8705739659634329013157482960027934795454950884941966136315983526808527784650002967954059125075894300750418062742140200130188545338806355927273170470295451
c2=1004454248332792626131205259568148422136121342421144637194771487691844257449866491626726822289975189661332527496380578001514976911349965774838476334431923162269315555654716024616432373992288127966016197043606785386738961886826177232627159894038652924267065612922880048963182518107479487219900530746076603182269336917003411508524223257315597473638623530380492690984112891827897831400759409394315311767776323920195436460284244090970865474530727893555217020636612445
N = p * q * r
d1 = gmpy2.invert(e, p - 1)
m1 = long_to_bytes(pow(c1, d1, p))
d2 = gmpy2.invert(e, (p - 1) * (q - 1) * (r - 1))
m2 = long_to_bytes(pow(c2, d2, N))
flag = m1 + m2
print(flag)
Week3
故事新编1
from hashlib import md5
zen1 = '''
'''
key1 = ''
def enc1(plaintext, key):
def shift_char(c, k):
return chr(((ord(c) - ord('A') + (ord(k) - ord('A'))) % 26) + ord('A'))
plaintext = plaintext.upper()
key = key.upper()
ciphertext = []
key_index = 0
for char in plaintext:
if char.isalpha():
ciphertext.append(shift_char(char, key[key_index % len(key)]))
key_index += 1
else:
ciphertext.append(char)
return ''.join(ciphertext)
print('enc = \'\'\'' + enc1(zen1, key1)+'\'\'\'')
flag = b'flag{'+md5(zen1.encode()).hexdigest().encode()+b'}'
print(flag)
#----------------------------------------------
enc = '''
TYBNBBZNT WF TYUMMK NAIB HYFZ.
XFIFBKWG AM CXBMYK BVNF CNITBWBB.
GVEJMX QL VXBHRJ NITV VIFXZRP.
WPFXEYQ QG OWNUXZ MBTV QBEJMBKTNXL.
TYSN JL JXNMMF GZUO GMLNXL.
GCSLTX QL VXBHRJ NITV WYGAS.
SDUHT QL PXOSAWLF
KMTXTJWYANZ VWNHMA.
GCWWJTT VULMG NJYO'M AIYVQOY WHPNOA NH JFRSE UAM KOEMG.
NDNIHCZB IZOPLCDTTBNR JSNLM QNZBNR.
MFEGLT LPHOEL BRNYS IILM LQZRFNMR.
CGFXAG RPJMBKBNEG GVDYOVMW.
'''
维吉尼亚密码板子题,用脚本解出密匙,带入尝试即可,沟槽的出题人没搞好文件让我一晚上没出这个题,于是乎第二天给出了:
题目提示:1. zen内全部为大写字符 2. zen末尾存在一个换行符
蓝的盆...
脚本如下
'''
维吉尼亚密码
'''
import math
def kasiski(ciphertext, t):
dict = {}
for i in range(len(ciphertext) - t + 1):
#每次遍历都会向右移动一个长度为t的字符串
item = ciphertext[i:i+t]
if item in dict:
continue
if ciphertext.count(item) > t:
dict[item] = []
j = i+t
while j <= len(ciphertext) - t + 1:
#从第二个item的位置开始找,如果找到的到返回索引,找不到就返回-1
pos = ciphertext.find(item,j)
if pos > 0:
dict[item].append(pos - i)
j = pos + t
else:
break
keylen = []
for item in dict:
x = math.gcd(dict[item][0],dict[item][1])
for i in dict[item][2:]:
x = math.gcd(x,i)
if x > 2:
keylen.append(x)
return keylen
'''
维吉尼亚密码已知密钥长度,爆破密钥
'''
def getkey(keylen,ciphertext):
#1.根据网上的对子a-z出现频率的统计,创建一个列表p,用于后面计算重合指数
p = [0.08167, 0.01492, 0.02782, 0.04253, 0.12702, 0.02228, 0.02015, 0.06094, 0.06966, 0.00153, 0.00772, 0.04025,
0.02406, 0.06749, 0.07507, 0.01929, 0.00095, 0.05987, 0.06327, 0.09056, 0.02758, 0.00978, 0.02360, 0.00150,
0.01974, 0.00074]
#2.根据密钥的长度对密文内容进行分组
for i in range(keylen):
f_sum_list = []
after_div = ciphertext[i::keylen].lower()
#5.设置for循环,计算偏移量(相当于凯撒单表解密)
for offset in range(26):
#3.分组以后统计各组a-z在各自组中出现的次数
alp_sta_list = []
for x in range(26):
alp_sta = after_div.count(chr(97+(x+offset)%26))
alp_sta_list.append(alp_sta)
# print(alp_sta_list)
#4.根据alp_sta_list和p计算重合指数f
f_sum = 0
for x in range(26):
f = (alp_sta_list[x]*p[x])/len(after_div)
f_sum = f_sum + f
f_sum_list.append(f_sum)
key = chr(97+f_sum_list.index(max(f_sum_list)))
print(key,end='')
if __name__ == '__main__':
# ciphertext = input('请输入明文: ')
t = 1
ciphertext = 'TYBNBBZNTWFTYUMMKNAIBHYFZXFIFBKWGAMCXBMYKBVNFCNITBWBBGVEJMXQLVXBHRJNITVVIFXZRPWPFXEYQQGOWNUXZMBTVQBEJMBKTNXLTYSNJLJXNMMFGZUOGMLNXLGCSLTXQLVXBHRJNITVWYGASSDUHTQLPXOSAWLFKMTXTJWYANZVWNHMAGCWWJTTVULMGNJYOMAIYVQOYWHPNOANHJFRSEUAMKOEMGNDNIHCZBIZOPLCDTTBNRJSNLMQNZBNRMFEGLTLPHOELBRNYSIILMLQZRFNMRCGFXAGRPJMBKBNEGGVDYOVMW'
for i in range(1, len(ciphertext)):
possible = kasiski(ciphertext, i)
for keylen in possible:
print("probable key", t, ": ", end='')
getkey(keylen,ciphertext)
print("")
t += 1
没e这能玩?
from Crypto.Util.number import *
import random
import sympy
import gmpy2
m = bytes_to_long(b'flag{*****}')
p = getPrime(512)
q = getPrime(512)
r = getPrime(512)
h1 = 1*p + 1*q + 1*r
h2 = 2*p + 3*q + 3*r
h3 = 9*p + 9*q + 6*r
print( "hint_of_pqr=" , h1 , h2 , h3 )
e = getPrime(64)
a_big_prime = getPrime( 512 )
hint = pow(a_big_prime,e,2**512)
print( "big_prime is: " , a_big_prime )
print( "hint is: " , hint )
n = p*q*r
c = pow( m , e , n )
print( "c=" , c )
"""
hint_of_pqr= 31142735238530997044538008977536563192992446755282526163704097825748037157617958329370018716097695151853567914689441893020256819531959835133410539308633497 83244528500940968089139246591338465098116598400576450028712055615289379610182828415628469144649133540240957232351546273836449824638227295064400834828714760 248913032538718194100308575844236838621741774207751338576000867909773931464854644505429950530402814602955352740032796855486666128271187734043696395254816172
big_prime is: 10340528340717085562564282159472606844701680435801531596688324657589080212070472855731542530063656135954245247693866580524183340161718349111409099098622379
hint is: 1117823254118009923270987314972815939020676918543320218102525712576467969401820234222225849595448982263008967497960941694470967789623418862506421153355571
c= 999238457633695875390868312148578206874085180328729864031502769160746939370358067645058746087858200698064715590068454781908941878234704745231616472500544299489072907525181954130042610756999951629214871917553371147513692253221476798612645630242018686268404850587754814930425513225710788525640827779311258012457828152843350882248473911459816471101547263923065978812349463656784597759143314955463199850172786928389414560476327593199154879575312027425152329247656310
"""
第一部分是一个解方程,第二部分是一个求离散对数,发现模数为 \(2^{512}\),因此一定是一个光滑数,所以考虑用 Pohlig_Hellman 算法求解。
from Crypto.Util.number import *
from gmpy2 import *
h1, h2, h3 = 31142735238530997044538008977536563192992446755282526163704097825748037157617958329370018716097695151853567914689441893020256819531959835133410539308633497, 83244528500940968089139246591338465098116598400576450028712055615289379610182828415628469144649133540240957232351546273836449824638227295064400834828714760, 248913032538718194100308575844236838621741774207751338576000867909773931464854644505429950530402814602955352740032796855486666128271187734043696395254816172
b = 10340528340717085562564282159472606844701680435801531596688324657589080212070472855731542530063656135954245247693866580524183340161718349111409099098622379
hint = 1117823254118009923270987314972815939020676918543320218102525712576467969401820234222225849595448982263008967497960941694470967789623418862506421153355571
c = 999238457633695875390868312148578206874085180328729864031502769160746939370358067645058746087858200698064715590068454781908941878234704745231616472500544299489072907525181954130042610756999951629214871917553371147513692253221476798612645630242018686268404850587754814930425513225710788525640827779311258012457828152843350882248473911459816471101547263923065978812349463656784597759143314955463199850172786928389414560476327593199154879575312027425152329247656310
p = 3 * h1 - h2
q = (h3 - 6 * h1) // 3 - p
r = h1 - p - q
n = p * q * r
# a^x = b (mod n) 在一个素数域上的解
def Pohlig_Hellman(a, b, n, p, e):
# 求一个 n 上的阶,n 为素数幂,阶必在幂上
for i in range(e):
if pow(a, pow(p, i, n), n) == 1:
e = i
break
x = 0
gamma = pow(a, pow(p, e - 1, n), n)
for i in range(e):
# (a^(-x) * h)^(p - k - 1) = gamma
h = pow(pow(a, -x, n) * b, pow(p, e - i - 1, n), n)
for j in range(p):
if pow(gamma, j, n) == h:
x += pow(p, i) * j
break
return x
e = Pohlig_Hellman(b, hint, 2^512, 2, 511)
d = gmpy2.invert(e, (p - 1) * (q - 1) * (r - 1))
m = pow(c, d, n)
print(long_to_bytes(int(m)))
不用谢喵
from Crypto.Cipher import AES
from Crypto.Util.number import *
import os
KEY = b"fake_key_fake_ke"
FLAG = "flag{fake_flag_fake_flag}"
def decrypt(c):
AES_ECB = AES.new(KEY, AES.MODE_ECB)
decrypted = AES_ECB.decrypt(long_to_bytes(c))
return decrypted.hex()
def encrypt():
iv = os.urandom(16)
AES_CBC = AES.new(KEY, AES.MODE_CBC, iv)
encrypted = AES_CBC.encrypt(FLAG.encode())
print('iv:',iv.hex())
return iv.hex() + encrypted.hex()
c=encrypt()
print('encrypt:',c)
print('decrypt:',decrypt(int(c,16)))
#encrypt: f2040fe3063a5b6c65f66e1d2bf47b4cddb206e4ddcf7524932d25e92d57d3468398730b59df851cbac6d65073f9e138
'''
decrypt: f9899749fec184d81afecd35da430bc394686e847d72141b3a955a4f6e920e7d91cb599d92ba2a6ba51860bb5b32f23b
'''
我们来看一下 ECB 加密方式和 CBC 加密方式的不同。
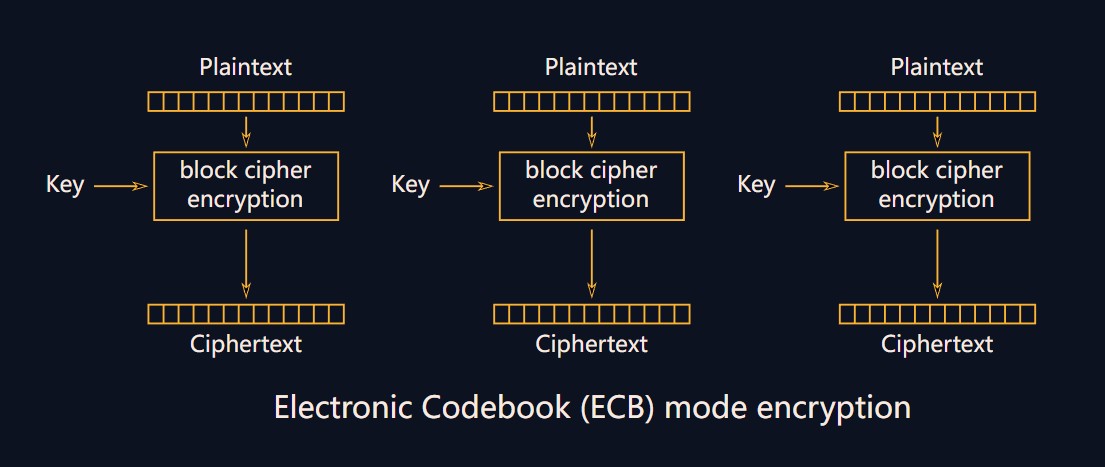
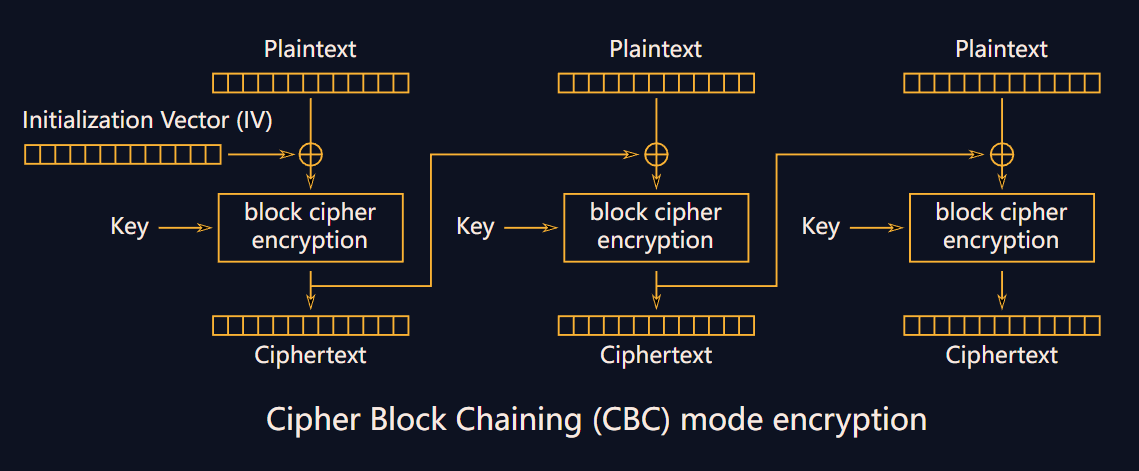
可以发现只有两个方式不同:
-
CBC初始化时第一个明文块异或一个随机向量 \(iv\)。 -
CBC加密的下一个明文块在加密前异或上一个密文块。
而题目已经将 \(iv\) 放在了 CBC 加密后密文的前 \(16\) 字节(向量数组只有 \(16\) 字节大小),因此我们得到向量后,对 ECB 解密后的第一个明文块进行异或就可以得到第一部分 \(flag\),第二部分 \(flag\) 只需要第一个密文块异或第二个明文块,最终得到完整 \(flag\)。
脚本如下
from Crypto.Util.number import *
from pwn import *
# CBC encrypt
E = 'f2040fe3063a5b6c65f66e1d2bf47b4cddb206e4ddcf7524932d25e92d57d3468398730b59df851cbac6d65073f9e138'
# ECB decrypt
D = 'f9899749fec184d81afecd35da430bc394686e847d72141b3a955a4f6e920e7d91cb599d92ba2a6ba51860bb5b32f23b'
E = bytes.fromhex(E)
D = bytes.fromhex(D)
iv = E[:16]
c1 = E[16:32]
c2 = E[32:48]
m1 = D[16:32]
m2 = D[32:48]
F1 = xor(m1, iv)
F2 = xor(m2, c1)
print(F1 + F2)
两只黄鹂鸣翠柳
import random
from Crypto.Util.number import *
while 1:
delta = getPrime(1024)
p = getPrime(512)
q = getPrime(512)
N = p * q
if delta<N:
break
flag = b'flag{xxxxxxxxxxxxx}'
e = getPrime(10)
m = bytes_to_long(flag)
t1 = random.randint(0,255)
t2 = random.randint(0,255)
assert (t1 != t2)
m1 = m + t1 * delta
m2 = m + t2 * delta
c1 = pow(m1, e, N)
c2 = pow(m2, e, N)
print("e = ", e)
print("c1 = ", c1)
print("c2 = ", c2)
print("N = ", N)
print("delta = ", delta)
'''
e = 683
c1 = 56853945083742777151835031127085909289912817644412648006229138906930565421892378967519263900695394136817683446007470305162870097813202468748688129362479266925957012681301414819970269973650684451738803658589294058625694805490606063729675884839653992735321514315629212636876171499519363523608999887425726764249
c2 = 89525609620932397106566856236086132400485172135214174799072934348236088959961943962724231813882442035846313820099772671290019212756417758068415966039157070499263567121772463544541730483766001321510822285099385342314147217002453558227066228845624286511538065701168003387942898754314450759220468473833228762416
N = 147146340154745985154200417058618375509429599847435251644724920667387711123859666574574555771448231548273485628643446732044692508506300681049465249342648733075298434604272203349484744618070620447136333438842371753842299030085718481197229655334445095544366125552367692411589662686093931538970765914004878579967
delta = 93400488537789082145777768934799642730988732687780405889371778084733689728835104694467426911976028935748405411688535952655119354582508139665395171450775071909328192306339433470956958987928467659858731316115874663323404280639312245482055741486933758398266423824044429533774224701791874211606968507262504865993
'''
由于 \(t_1,t_2\) 是可以爆破的,而 \((m + t_1\delta)^e - c_1\),\((m + t_2\delta)^e - c_2\) 为两个 \(e\) 次多项式,由于他们的根是相同的,我们只想求出一组 \(m + a = 0\) 即可,考虑多项式 \(\gcd\),如果两个多项式的 \(\gcd\) 不为 \(1\),那么说明他们有共同的根,因此我们不妨设 \(x = m + t_2\delta\),那么 \(m + t_1\delta = i\delta + m + t_2\delta(i \in [-255, 255])\),爆破 \(t_1\) 解出一个不为 \(1\) 的根,然后爆破 \(t_2\) 求解。
脚本如下
from Crypto.Util.number import *
from gmpy2 import *
from tqdm import *
e = 683
c1 = 56853945083742777151835031127085909289912817644412648006229138906930565421892378967519263900695394136817683446007470305162870097813202468748688129362479266925957012681301414819970269973650684451738803658589294058625694805490606063729675884839653992735321514315629212636876171499519363523608999887425726764249
c2 = 89525609620932397106566856236086132400485172135214174799072934348236088959961943962724231813882442035846313820099772671290019212756417758068415966039157070499263567121772463544541730483766001321510822285099385342314147217002453558227066228845624286511538065701168003387942898754314450759220468473833228762416
N = 147146340154745985154200417058618375509429599847435251644724920667387711123859666574574555771448231548273485628643446732044692508506300681049465249342648733075298434604272203349484744618070620447136333438842371753842299030085718481197229655334445095544366125552367692411589662686093931538970765914004878579967
delta = 93400488537789082145777768934799642730988732687780405889371778084733689728835104694467426911976028935748405411688535952655119354582508139665395171450775071909328192306339433470956958987928467659858731316115874663323404280639312245482055741486933758398266423824044429533774224701791874211606968507262504865993
def gcd(g1, g2):
while g2:
g1, g2 = g2, g1 % g2
return g1.monic()
PR.<x> = PolynomialRing(Zmod(N))
for i in trange(-255, 256):
f1 = (x + i * delta)^e - c1
f2 = (x)^e - c2
res = gcd(f1, f2).coefficients()[0]
if (res != 1):
res = -res
else:
continue
print(res)
for j in range(-255, 256):
m = (res + j * delta) % N
flag = long_to_bytes(int(m))
if (b'flag' in flag):
print(flag)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号