20172314 2018-2019-1《程序设计与数据结构》第六周学习总结
教材学习内容总结
概述
-
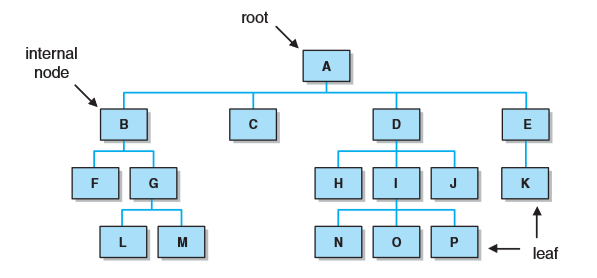
树是一种非线性结构,其元素被组织成一个层次结构。即n个结点组成的有限集合。
-
树由结点和边构成,树的根位于树顶层的唯一结点。
-
位于树中较低层的结点是上一层的孩子
同一双亲的两个节点称为兄弟
没有任何孩子的结点称为叶子
一个至少含有一个孩子的非根结点称为一个内部结点
根是树中所有结点的祖先,沿着某一特定结点的路径可到达的结点是该结点的子孙。
-
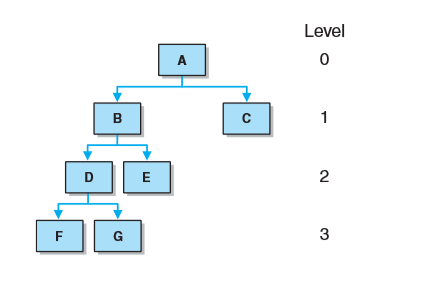
结点的层就是从根节点到该结点的路径长度。从根到该结点 的边数目就是其路径长度。
-
树的高度是指从根到叶子之间最远路径的长度。
树中任一结点可以具有的最大孩子数目为该树的度。
对结点所含有的孩子数目无限制的树称为广义树。
每个节点限制为不超过n个孩子的树称为一棵n元树。
节点最多含有两个孩子的树称为二叉树。
树的所有叶子都位于同一层或相差不超过两层,就称该树是平衡的。
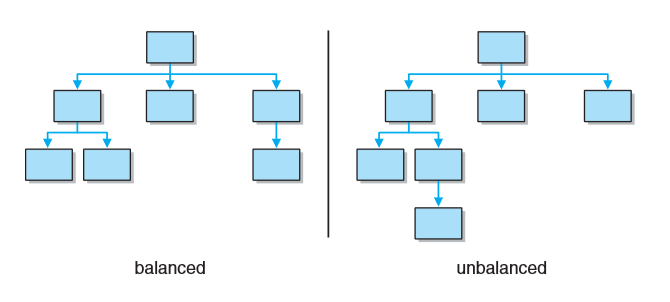
如果树是平衡的且底层所有叶子都位于树的左边,则认为该树是完全的。(即满二叉树去掉最下层右边的若干个结点)。
如果一个n元树的所有叶子都位于同一层且每一结点要么是一片叶子要么正好具有n个孩子,则称该树是满的。(满二叉树是特殊的完全二叉树)。
-
二叉树的第i层最多有2^(i-1)个结点
-
深度为k的二叉树最多有(2^k)-1个结点
-
具有n个结点的完全二叉树的高度为(log2n)+1。
实现树的策略
-
计算策略
- 将元素n的左孩子置于位置(2n+1),将元素的右孩子置于(2(n+1))。就是从根节点开始,往下依次分别计算左右孩子的位置,然后填入数组中。
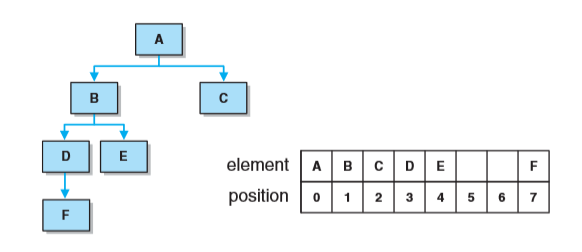
- 将元素n的左孩子置于位置(2n+1),将元素的右孩子置于(2(n+1))。就是从根节点开始,往下依次分别计算左右孩子的位置,然后填入数组中。
-
链接策略
- 按照先来先服务的基准连续分配数组位置,而不是通过其在树中的定位将树元素指派到数组位置上,且不用考虑该树的完全性。每一结点存储的是每一个孩子的数组索引。数组中元素的顺序仅仅由它们进入该树的顺序决定。假设下图进入顺序为A C B E D F,那么其数组索引依次是0 1 2 3 4 5,A的孩子是B C,所以A中储存2 1 ,以此类推。
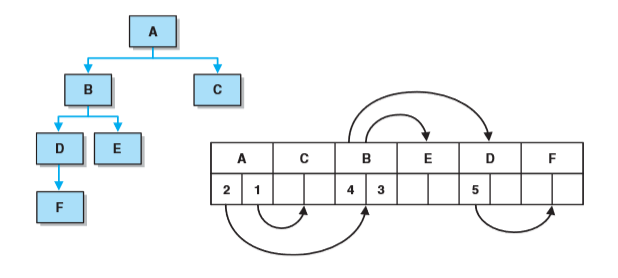
- 按照先来先服务的基准连续分配数组位置,而不是通过其在树中的定位将树元素指派到数组位置上,且不用考虑该树的完全性。每一结点存储的是每一个孩子的数组索引。数组中元素的顺序仅仅由它们进入该树的顺序决定。假设下图进入顺序为A C B E D F,那么其数组索引依次是0 1 2 3 4 5,A的孩子是B C,所以A中储存2 1 ,以此类推。
-
两者的选择:如果树不完全或只是相对完全,计算策略会为不包含数据的树位置分配空间 ,容易浪费大量空间;模拟策略不会浪费空间,允许连续分配数组位置,但是增加了删除树中元素的成本,因为需要对剩余元素进行移位或保留一个空闲列表。
-
一棵含有m个元素的平衡n元树具有的高度为lognm。
-
树可以比线性结构更有效,但树有其特有的成本,n相对较小时,树和线性结构并不存在显著差别,当n越来越大时,树的效率就显现出来。
树的遍历
-
前序遍历
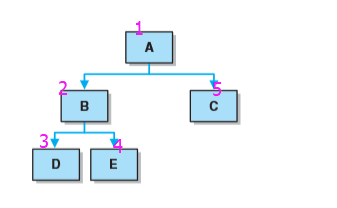
- 从根结点开始,访问每一结点及其孩子。沿某一路径访问直到其没有孩子时,返回访问其兄弟。
- 顺序如图为:A B D E C
-
中序遍历
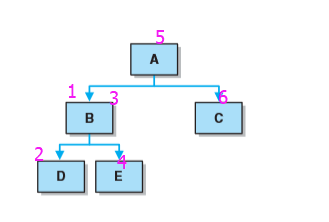
- 从根开始访问结点左边的孩子,然后是结点,再然后是任何剩余结点。他是从中间开始访问的,并且当某一结点没有任何剩余孩子时,会返回到前一节点。
- 如图顺序为:D B E A C
-
后序结点
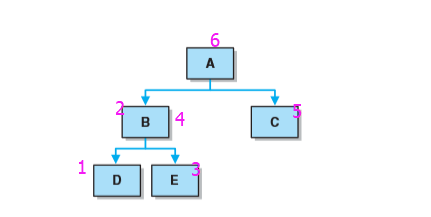
- 从根结点开始,访问结点的孩子,然后是该结点。首先访问的是没有任何孩子的结点,然后逐步向前返回访问其他的孩子。
- 如图顺序为D E B C A
-
层序遍历
- 从根结点开始,访问每一层的所有结点,一次一层。每一层先访问左孩子后访问右孩子。
- 如图顺序为:A B C D E
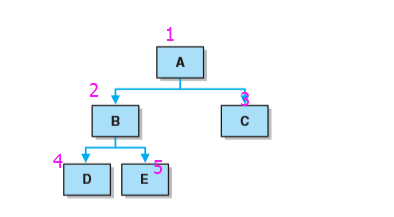
二叉树
- 二叉树的操作
- getRoot:返回指向二叉树根的引用
- ieEmpty:判断该树是否为空
- size:判断树中元素数目
- contains:判断指定目标是否在树中
- find:如果找到该元素,则返回指向其的引用
- toString:返树的字符串表示
- iteratorInOrder:为树的中序遍历返回一个迭代器
- iteratorPreOrder:为树的前序遍历返回一个迭代器
- iteratorPostOrder:为树的后序遍历返回一个迭代器
- iteratorLevelOrder:为树的层序遍历返回一个迭代器
- BinaryTreeADT接口

使用二叉树:表达式树
-
表达式树的根及其内部结点包含着操作,且所有叶子也包含着操作数。对表达式树的求值是从下往上的。

-
Postfix类和PostfixEvaluator类的理解图示更清楚,对于操作数,建立一个新的ExpressionTreeObj,构造一个ExoressionTree压入栈中,遇到操作符,弹出栈顶的两个ExpressionTrees,使用该操作符建立一个新的ExpressionTree压入栈中。并且需要注意的是,该表达式树栈的栈顶位于右边。
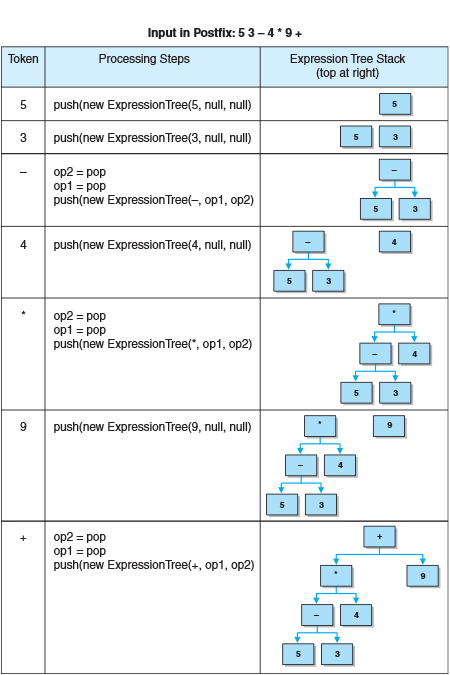
Postfix类的UML描述
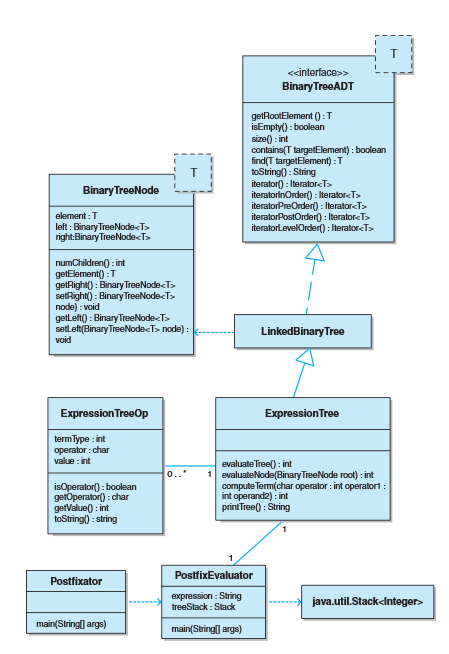
背部疼痛诊断器
- 决策树:结点表示决策点,子结点表示在该决策点的可选项。决策树的叶结点表示可能的推断,这些推断是基于答案得出的。
- 简单决策树(只有是和否)可以用二叉树来建模。进行一个诊断时,从根结点的问题开始,根据答案直到到达叶结点为止。
- 决策树有时候用作专家系统的基础,专家系统是一种软件,用于尝试表示某个领域的专家知识。
- 背部疼痛诊断决策树
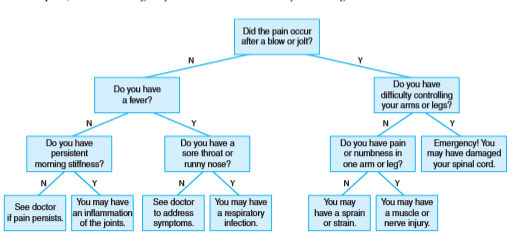
用链表实现二叉树
-
构造函数应处理两种情况:
- 创建一棵空二叉树
- 用单个元素(但没有孩子)创建一棵二叉树
-
BinaryTreeNode类负责跟踪储存在每个位置上的元素,以及指向每个结点的左右子树或孩子的指针。
-
实现树结点或二叉树结点类的其他可能:
- 用包含方法来测试某结点是否为叶子或内部结点(有没有至少一个孩子),测试从根到该结点的深度,或计算左右子树的高度。
- 使用多态性,创建各种实现,如emptyTreeNode,innerTreeNode,leafTreeNode,他们可以区分各种可能性。
-
find方法
- 通过使用存储在树中的类的equals方法来判定等同性,来遍历该树。
- findAgain方法可以用来区分find方法的第一个实例和随后的每个调用。
-
iteratorInOrder方法
允许一个用户类在中序遍历中单步遍历树的元素,提供了使用一个集合来构建另一个集合的另一个例子。
教材学习中的问题和解决过程
-
问题一:用链表实现二叉树的find方法和findAgain书上说可以区分find方法的第一个实例和随后的每个调用,并不是很理解。
-
问题一解决:由于findAgain方法使用了递归,他就需要使用一个私有支持方法,因为第一个调用和随后每个调用的签名和行为可能是不相同的。那就是说,如果没有findAgain方法中的递归部分,那么find方法就只能用来查找根结点,如果要查找内部结点的话,就需要使用递归部分,单纯用find方法需要很复杂的程序实现。
-
问题二:书上代码ExpressionTree中的printTree有点复杂,较难理解。
-
问题二解答:首先上网查找了一下部分代码希望能找到解释,然后就找到了侯泽洋同学的博客...里面有同样的问题。然后他给我讲解了一下具体思路。我把我的理解在代码中进行了注释。
public String printTree() { UnorderedListADT<BinaryTreeNode<ExpressionTreeOp>> nodes = new ArrayUnorderedList<BinaryTreeNode<ExpressionTreeOp>>(); UnorderedListADT<Integer> levelList = new ArrayUnorderedList<Integer>(); BinaryTreeNode<ExpressionTreeOp> current; String result = ""; int printDepth = this.getHeight();//树的高度 int possibleNodes = (int) Math.pow(2, printDepth + 1);//由于根节点位置是0,最下层是第printDepth+1层,这个二叉树可能的总结点数就是2的printDepth+1次方 int countNodes = 0;//结点数目 nodes.addToRear(root);//在无序列表中添加根部结点 Integer currentLevel = 0;//当前层 Integer previousLevel = -1;//前一层 levelList.addToRear(currentLevel);//把当前层添加到层数链表中 while (countNodes < possibleNodes) {//此树不满时 countNodes = countNodes + 1;//从0开始加 current = nodes.removeFirst();//把第一个数取出来 currentLevel = levelList.removeFirst();//设置成当前层数 if (currentLevel > previousLevel) {//如果不在同一层就换行 result = result + "\n\n";//进行换行 previousLevel = currentLevel;//层数下移 for (int j = 0; j < ((Math.pow(2, (printDepth - currentLevel))) - 1); j++) result = result + " ";//每一层加空格,第n层有2^(n-1)个数 } else {//如果在同一行,每两个数之间加空格 for (int i = 0; i < (Math.pow(2, (printDepth - currentLevel + 1)) - 1); i++) { result = result + " "; } } if (current != null) {//如果当前结点不为空,记录他的左右孩子,并增加层数 result = result + (current.getElement()).toString(); nodes.addToRear(current.getLeft()); levelList.addToRear(currentLevel + 1); nodes.addToRear(current.getRight()); levelList.addToRear(currentLevel + 1); } else {//如果当前结点为空,给他分配空间,存一个null进去 nodes.addToRear(null); levelList.addToRear(currentLevel + 1); nodes.addToRear(null); levelList.addToRear(currentLevel + 1); result = result + " "; } } return result; }
代码调试中的问题和解决过程
-
问题一:实例化LinkedBinaryTree时,如果使用构造函数
public LinkedBinaryTree(T element, LinkedBinaryTree<T> left, LinkedBinaryTree<T> right) { root = new BinaryTreeNode<T>(element); root.setLeft(left.root); root.setRight(right.root); }当某个参数为空时,如图,就不能运行,产生空指针的错误提示。
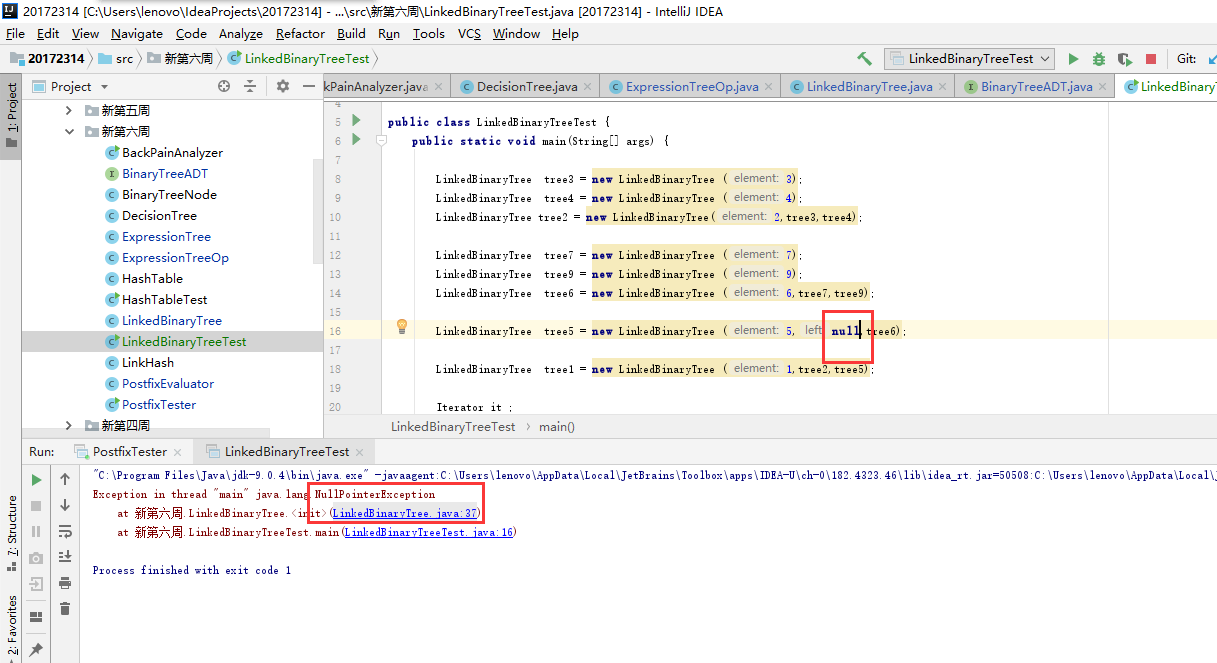
-
问题一解决:我开始的时候认为参数有null可以是一个空位,但运行出现空指针错误,然后把参数改为确定的数后就不出错了...其实是一个很低级的错误,参数为空的话就没有指针了,当然不能运行(▼ヘ▼#)
-
问题二:当树中没有要查找的结点时,由于我的contain方法中使用到了find方法,当找不到时,就抛出异常,程序终止了。
public boolean contains(T targetment) { if(find(targetment) != null) return true; return false; }如图
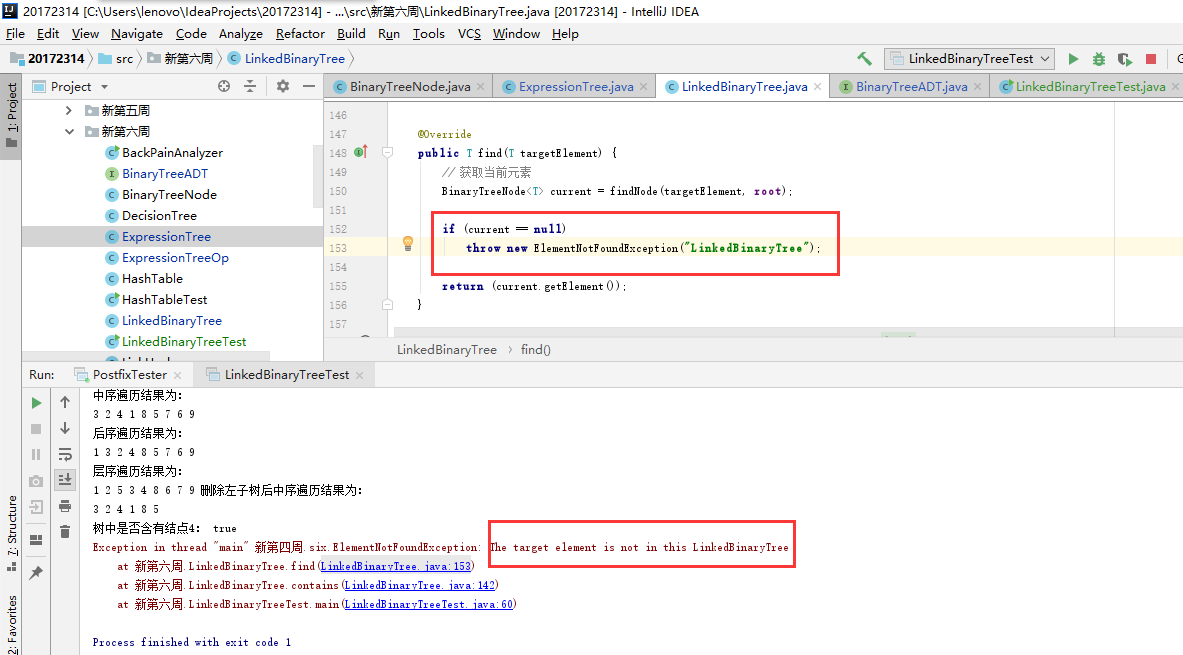
-
问题二解决:首先想到把find方法中的
if (current == null) throw new ElementNotFoundException("LinkedBinaryTree");改为
if (current == null) return null;这样正好符合contains方法的需求,但是有一点小问题就是更改了find方法后,如果单纯的使用find方法去查找一个不存在的数,那么得到的是一个null,程序并不会终止,但我感觉问题不大,嘿嘿。
-
问题三:不知道如何打印一棵树
-
问题三解决:首先想到在表达树的代码中有printTree方法,原理应该是一模一样的,但是不能直接拿来用,因为它在打印表达树时,
UnorderedListADT<BinaryTreeNode<ExpressionTreeOp>> nodes = new ArrayUnorderedList<BinaryTreeNode<ExpressionTreeOp>>();
BinaryTreeNode<ExpressionTreeOp> current;
参数均为ExpressionTreeOp,而其中既有操作数又有操作符,而在二叉树的打印中只有数字结点,且有如图冲突

所以只需要把他改为泛型即可打印任意树。
UnorderedListADT<BinaryTreeNode<T>> nodes = new ArrayUnorderedList<BinaryTreeNode<T>>();
BinaryTreeNode<T> current; -
问题四:在做哈希表的实验时,链表出现错误
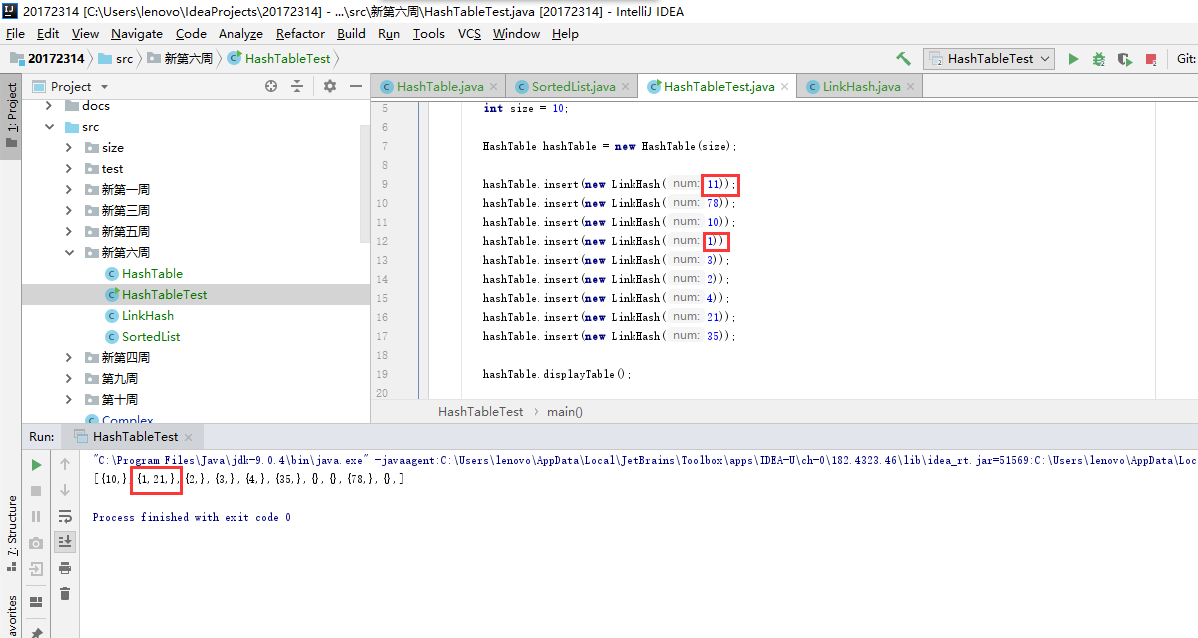
-
问题四解决:首先在每次插入链表后进行输出,找到了错误的地方

如图可见,当出现冲突的时候,会丢失原本在那个位置的数,所以就是insert方法中处理冲突的代码有错,检查代码后发现
public void insert(LinkHash link) { int data = link.getData(); LinkHash previous = null; LinkHash current = first; while(current!=null&&data>current.getData()) previous = current; current = current.next; count++; alltime++; } if (previous == null) { first = link; alltime++; } else { previous.next = link; link.next = current; //count++; alltime++; } }while循环的条件
while(current!=null&&data>current.getData())是错误的,有冲突的那个位置形成的链表是按先后顺序排的,并不需要从小到大,所以说当1进去时,他比11小,所以直接执行else操作,就丢失原来的11了。应把条件改为while (current != null)即可。
代码托管
上周考试错题总结
没有错题
结对及互评
- 20172305谭鑫谭鑫的博客一如既往的优秀,坚持不懈,每次记录的都很详细,对问题解决过程的每一步都有分析,给大佬抱拳。
- 20172323王禹涵王禹涵的博客跟我有一样的问题,就是那个printTree方法的理解,看他写的很详细。博客中关于解决问题的过程越来越详细了,博客质量稳步提升。还有就是突然发现王禹涵越来越专业了xswl
其他
这周对于树的学习属于拨云见日吧。想起来刚开始学Java的时候,我就在博客中写过,单纯的看书看完后容易一脸懵逼,这时候就选择直接分析代码,现在我又回到了当时的状态,刚看完书的时候怎么也理解不了一些方法,后来直接做pp,尝试摸索一下就理解很多知识点。哎,Java这东西不能太较真,随他去吧。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | |
|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 |
| 第一周 | 0/0 | 1/1 | 8/8 |
| 第二周 | 1163/1163 | 1/2 | 15/23 |
| 第三周 | 774/1937 | 1/3 | 12/50 |
| 第四周 | 3596/5569 | 2/5 | 12/62 |
| 第五周 | 3329/8898 | 2/7 | 12/74 |
| 第六周 | 4541/13439 | 3/10 | 12/86 |



