P9921 [POI 2023/2024 R1] Budowa lotniska

思路

\(m=1\) 详见别的题解。

\(m=2\) 时我们二分答案长度，考虑如何 check：只需 \(O(n^2)\) 枚举第一条长链端点和方向（左和上即可），接着看图：

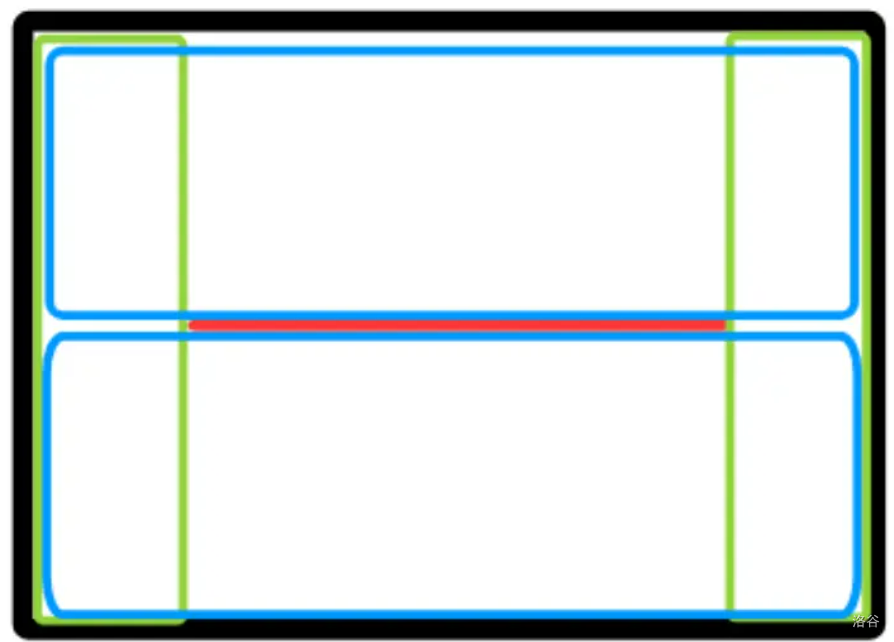
我们可以判断四个长方形内有无另一条不交于第一条的长链。

好，那么问题变成如何预处理长方形里前后缀的最长长度：

如：列的前缀最长链。

for(int j=1;j<=n;++j){
		l1[j]=l1[j-1];
		for(int x=1;x<=n;++x){
			int y=j;
			if(x-up[x][y]+1>=1)l1[j]=max(l1[j],up[x][y]);
			if(y-lf[x][y]+1>=1)l1[j]=max(l1[j],lf[x][y]);
		}
	}

可以做到 \(O(n^2)\) 转移。即枚举列，每次新加进来列时，用该列上点为端点贡献 出的长度更新信息。当然注意边界条件，详见代码。

code

#include<bits/stdc++.h>
using namespace std;
const int N=2000;
int n,a[N][N],m;
int lf[N][N],up[N][N];
int l1[N]/*前j列*/,l2[N]/*后j列*/,h1[N]/*前i行*/,h2[N]/*后i行最长lens*/; 
inline int init(){
	for(int j=1;j<=n;++j){
		l1[j]=l1[j-1];
		for(int x=1;x<=n;++x){
			int y=j;
			if(x-up[x][y]+1>=1)l1[j]=max(l1[j],up[x][y]);
			if(y-lf[x][y]+1>=1)l1[j]=max(l1[j],lf[x][y]);
		}
	}
	for(int j=n;j>=1;--j){
		l2[j]=l2[j+1];
		for(int x=1;x<=n;++x){
			int y=j;
			if(x-up[x][y]+1>=1)l2[j]=max(l2[j],up[x][y]);
			if(y-lf[x][y]+1>=j)l2[j]=max(l2[j],lf[x][y]);
			else l2[j]=max(l2[j],y-j+1);
		}
	}
	for(int i=1;i<=n;++i){
		h1[i]=h1[i-1];
		int x=i;
		for(int y=1;y<=n;++y){
			if(x-up[x][y]+1>=1)h1[i]=max(h1[i],up[x][y]);
			if(y-lf[x][y]+1>=1)h1[i]=max(h1[i],lf[x][y]);
		}
	} 
	for(int i=n;i>=1;--i){
		h2[i]=h2[i+1];
		int x=i;
		for(int y=1;y<=n;++y){
			if(x-up[x][y]+1>=i)h2[i]=max(h2[i],up[x][y]);
			else h2[i]=max(h2[i],x-i+1);
			if(y-lf[x][y]+1>=1)h2[i]=max(h2[i],lf[x][y]);
		}
	}
	return 0;
}
inline int check(int l){
	for(int i=1;i<=n;++i){
		for(int j=1;j<=n;++j){
			if(((j-l>=1&&l1[j-l]>=l)||(j+1<=n&&l2[j+1]>=l)||h1[i-1]>=l||h2[i+1]>=l)&&lf[i][j]>=l)return 1;
			if((l1[j-1]>=l||l2[j+1]>=l||(i-l>=1&&h1[i-l]>=l)||(i+1<=n&&h2[i+1]>=l))&&up[i][j]>=l)return 1;
		}
	}
	return 0;
}
int main(){
	ios::sync_with_stdio(0),cin.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;++i){
		for(int j=1;j<=n;++j){
			char c;
			cin>>c;
			a[i][j]=(c=='X');
		}
	}
	int ans=0;
	for(int i=1;i<=n;++i){
		for(int j=1;j<=n;++j){
			if(a[i][j]==0)lf[i][j]=lf[i][j-1]+1,up[i][j]=up[i-1][j]+1;
			else lf[i][j]=up[i][j]=0;
			ans=max({ans,lf[i][j],up[i][j]});
		}
	}
	if(m==1){
		cout<<ans;
		return 0;
	}
	init();
	int L=0,R=ans;
	ans=0;
	while(L<=R){
		int mid=L+R>>1;
		if(check(mid))ans=mid,L=mid+1;
		else R=mid-1;
	}
	cout<<ans;
	return 0;
}
/*
5 2
.X...
.XXXX
XX...
.....
.X.X.
*/

后记

刚开始写了个 \(O(n^4\log n)\) 的，结果比后来写的 \(O(n^2\log n+n^3)\) 快?